3.2. Понятие оптимальности по Слейтеру и Парето

Рассмотрим понятие оптимальности в смысле Парето и в смысле Слейтера. В случае однокритериальной задачи оба эти понятия совпадают с обычным понятием оптимальности. Введем эти понятия.

Рассмотрим задачу _i(x)  min, i M, при ограниченияхxX,X Rⁿ,M –конечное множество.

Введем следующие понятия и определения.

На множестве Х зададим отношение предпочтенияСлейтера и предпочтения Парето.

Определение 2.9.Пустьx,y X, будем говорить, чтоxпредпочтительнееy

а) по Парето и записывать тогда и только тогда, когда_K(x)_K(y) для всех KM, и существуютK, для которых эти неравенства строгие.

б) по Слейтеру и записывать тогда и только тогда, когда_K(x)_K(y) для всехKM.

В зависимости от того, какое будет взято на Хпредпочтение, возникают различные определения оптимальных точек.

Определение 2.10.Точкух^*будем называть точкой локального оптимума по Парето (Слейтеру), если существует такое₀>0, что для всех(0,₀) на множестве 0_(x₀)X не содержатся точки ().

Определение 2.11. Множество всех точек локального оптимума по Парето (Слейтеру) назовем локальным множеством Парето (Слейтера).

Определение 2.12.Точкух^*будем называть точкой глобального оптимума по Парето (Слейтеру), если вХне существует точекхтаких, что ().

Множество всех таких точек будем называть множеством Парето (Слейтера).

Точки глобального оптимума будем называть просто точками оптимума. Множество Р– Парето содержится во множествеS– Слейтера. Действительно, еслих^*ÎР, т.е. вХне существует такогох, что. Но тогда тем более не существует , т.е. х^*ÎS.Обратное, вообще говоря, не верно.

В случае, когда функции _i(x), iM, выпуклые, множествоXтакже выпуклое, множества локального и глобального оптимума совпадают. Можно показать, чтоРS.

3.3. Возможные (допустимые) и подходящие направления.

Определение 2.13.Направление (вектор)s0_n называется возможным (допустимым) в точкехХ, если существует такое₀ >0, что для всех [0, l₀] выполняетсях+lsÎX.

На рис. 2.6 показаны примеры возможных направлений.

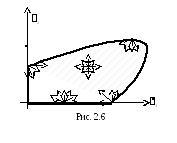
Множество возможных направлений образует конус, который мы будем обозначать через К_р (х).

Определение 2.14. Возможное направлениеsв точкехХ назовемподходящимпо Парето (Слейтеру), если существует₀ >0 такое, что для всех[0, l₀] справедливо.()

Множество подходящих по Парето и подходящих по Слейтеру направлений образуют конусы, которые обозначим соответственно К_p^p(x) иK_p^s(x)^., причемK_p^s(x) К_p^p(x), обратное, вообще говоря, не справедливо.

Определение 2.15. Функцию ⁰(x) назовем постоянной в точкех по направлениюs, если существует₀ >0 такое, что для всехΠ[0,l₀) функция ⁰(x+ls)= (x).

Определение.2.16.Будем говорить, что функции_i(x), iM, удовлетворяют условиюрегулярности R1(M), если для любыхх Rⁿ _, sRⁿиiM_i(x) не является постоянной.

Замечание.Если функции_i(x),iM, удовлетворяют условию регулярности R1(M), то предпочтения по Слейтеру и Парето можно не различать. Если |M| = 1, то понятие предпочтения по Слейтеру и Парето можно не различать и при нарушении условия. Это вытекает из определения этих предпочтений.

Теорема.2 14.ПустьХ– выпуклое множество. Для того, чтобых^*Хбыло точкой локального оптимума Парето (Слейтера) необходимо, чтобыK_p^p(х^*) = (K_p^s(х^*) = ).

Теорема. 2.15.Если_i(x), i M выпуклые функции,Х– выпуклое множество, тогда любая точка локального оптимума, как по Парето, так и по Слейтеру, будет точкой глобального оптимума.