konspect_2010

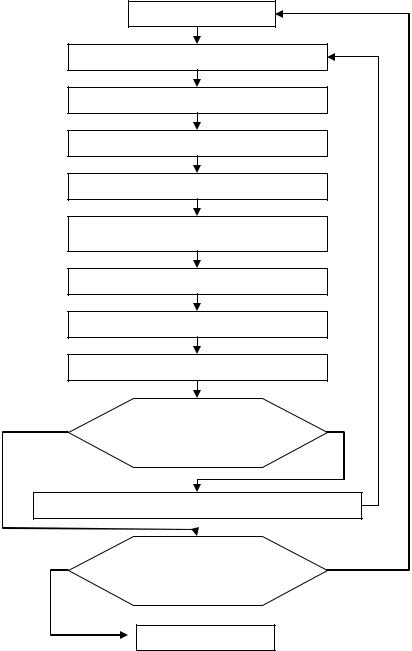
1 Постановка задачі

2Формування множини допустимих рішень

3Формування набору критеріїв

4Розробка шкал оцінювання критеріїв

5Оцінка допустимих варіантів критеріїв

6Оцінка та уточнення інформації щодо пріоритетів

7Побудова правил для рішення

8Впорядкування допустимих варіантів рішень

9Аналіз результатів впорядкування

11 Аналіз причин незадовільності та необхідний вид коректив

Кінець розв’язку задачі

Рисунок 10 - Структура процесу прийняття рішення

На 2 етапі формується безліч варіантів рішення, перевіряється можливість досягнення поставленої мети. Установлюється поняття «допустимість», розробляється спосіб перевірки допустимості, виділяється безліч варіантів рішення.

У блоці 3 аналізуються можливі наслідки обраних варіантів рішень, визначаються показники, які характеризують можливі наслідки, формується набір критеріїв для оцінки наслідків, розробляються шкали оцінювання критеріїв (блок 4).

Реалізація 3 й 4 етапів тісно зв'язана між собою. Під час розробки шкал оцінювання може виявитися незначний вплив одного із критеріїв, неоднорідність оцінювання, може виявитися комплексний характер одного

50

із критеріїв. У цих випадках доцільно повернутися до блоку 3 і скорегувати критерії.

На 5 етапі оцінюють припустимі варіанти рішень. На цьому етапі також може виникнути неоднозначний комплексний характер критеріїв, надлишкова детальність оцінок, невідповідність змісту деяких критеріїв їхнім шкалам. Для цього вносяться відповідні корективи в безліч критеріїв або шкал оцінювання.

Побудова вирішального правила, що приводить до необхідного впорядкування варіантів рішення, можлива протягом декількох етапів. На кожному з таких етапів одержують певну інформацію щодо пріоритету суб'єкта управління (блок 6). У блоці 7 інформація використовується для побудови відповідного вирішального правила.

Блок 8 – здійснюється порівняння й упорядкування варіантів рішення.

Блок 9 – аналіз результатів упорядкування. Під час такого аналізу може виявитися незадовільний результат (блок 10), тобто невідповідність упорядкування уявленням суб'єкта управління, тоді блок 11 – дослідження причини невідповідності.

Причини невідповідності:

1 Неадекватність використання інформації або допущень інтуїтивним пріоритетам.

2Випадання з аналізу якогось із припустимих варіантів рішень.

3Неповнота наборів критеріїв.

4Невідповідність шкал критеріїв можливостям оцінці.

5Неточності або помилки при оцінюванні деяких допустимих варіантів.

6Неточне визначення поняття допустимих варіантів.

Залежно від причин незадовільного впорядкування варіантів рішення до моделі вносяться необхідні уточнення, виправлення й доповнення й повторюються відповідні етапи.

Якщо впорядкування варіантів виявиться задовільним (блок 10), то при використанні вирішальних правил перевіряється, чи відповідає його вид поставленому завданню (блок 12).

Наприклад, у поставленому завданні необхідно лінійно впорядкувати припустимі варіанти рішення, у той же час, вирішальне правило призводить лише до їхнього часткового впорядкування, тоді необхідно одержати додаткову інформацію щодо пріоритету (повернення до блоку 6), побудувати нове більш жорстке вирішальне правило. Цю процедуру повторювати доти, поки не буде вичерпана вся додаткова інформація. При неможливості одержання додаткової інформації, початкова постановка задачі повинна бути менш жорсткою.

Коли впорядкування варіантів рішень визнається суб'єктом управління як задовільне, то воно вважається остаточним.

51

1.5.3 Постановка багатокритеріальної задачі

Багатокритеріальна задача оптимального управління подана тройкою U , , R , де U – множина управлінь, – відображення U в просторі доходів Em ; R – бінарне відношення на Em , за яким доходи

порівнюються.

Постановка задачі та її властивості

Нехай U – множина управлінь для деякого об’єкта. Управління u U можуть мати різну природу: стратегії в грі, неперервні функції, правила зупинки. Природа та структура множин U для загальної постановки задачі оптимального управління несуттєві. Кожному управлінню u U ставиться у відповідність m -мірний вектор доходу (u) Em . Вид визначається

властивостями об’єкта управління. Будемо інтерпретувати Em як простір

доходів.

Замість доходів можна розглядати штрафи. У першому випадку оптимальні управління будуть відповідати мажорантам, в іншому – мінорантам; обидва випадки еквівалентні один одному, тому далі будемо розглядати доходи.

Нехай на просторі Em задане бінарне відношення. Управління u* U

являється оптимальним, якщо за всіма іншими управліннями u U неможливо отримати вектор доходів (u) , який має більшу перевагу у

Багатокритеріальна задача оптимального управління полягає в тому, щоб при заданих U , та R виділити (U ) . Якщо відображення зіставляє кожному u U число (u) E1 , а відношення R являється відношенням „більше‖ на множині дійсних чисел, то отримаємо класичну однокритеріальну задачу оптимального управління.

Багатокритеріальна задача оптимального управління звичайно має

окремим розв’язком – будь-яке R -оптимальне управління u* U . Специфіка задачі може привести до того, що стає необов’язковим

виділення множини (U ) : достатньо знайти хоч один елемент u (U ) чи частину (U ) , яка характеризується деякими додатковими властивостями.

Ситуація прийняття багатоцільових рішень характеризується парою {x,F}, де x={x1,..xm} – безліч рішень суб'єктів управління, F={F1,F2,…,FQ}={fkq}Q,m, (q,k=1) – вектор функціонала оцінювань. Необхідно вибрати єдине рішення, що буде оптимальним за критерієм згортки з урахуванням впливу факторів (v, w, u) , де

v – метод нормалізації;

52

u – співвідношення пріоритету; w – критерій згортки.

Метод нормалізації – це функція переходу F, як однозначного відображення RQ в Rl, нормалізація використовується для переходу до порівняльних шкал у значеннях функціонала оцінювання (табл. 16).

Метод пріоритету – вектор оцінок (u1,…uQ) на компонентах

F={F1,F2,…,FQ} (табл. 17).

Критерій згортки – принцип прийняття оптимальних рішень або функція відображення RQ в Rl (табл. 18).

Таблиця 16 - Методи нормалізації

Таблиця 17Принципи побудови пріоритетів

Таблиця 18 - Критерій згортки

53

1.5.4 Багатокритеріальна модель обґрунтування прийняття рішень [11]

Одноцільова багатокритеріальна модель обґрунтування прийняття рішень у полі однієї інформаційної ситуації

За наявності однієї цілі (одного цільового функціонала оцінювання) у полі вибраної інформаційної ситуації актуальною стає проблема обґрунтування прийняття рішення, яке є компромісним щодо кількох критеріїв оптимальності (характерних для даної інформаційної ситуації) [11].

У цьому випадку обґрунтування прийняття рішення доцільно здійснювати згідно з ієрархічною моделлю (схемою), наведеною на рисунку 11.

Зазначимо, що реалізація цієї й подальших ієрархічних моделей базується на використанні так званої операції «згортки інформації». Формально під методом (оператором) згортки інформації, що відповідає певному критерію, будемо розуміти внутрішню частину цього критерію, яка здійснює перетворення початкової інформації до вигляду, зручного щодо застосування критеріїв обґрунтування прийняття рішення.

K

Цю операцію позначимо таким чином: « » , де К — це ознака критерію, на основі якого здійснюють згортку.

На рис. 10 використано такі умовні позначення:

K qj — оператори згортки функціонала оцінювання Р, які

відповідають критеріям обґрунтування прийняття рішень, що використовуються в полі інформаційної ситуації I j , ( j 1,..., 5; q 1,..., Q j ) ;

НОРМ— оператор нормалізації матриці FI j ;

FI H — нормалізована матриця;

j

54

інформаційної ситуації I j .

Рисунок 11 – Ієрархічна модель обґрунтування прийняття одноцільового багатокритеріального рішення у полі однієї інформаційної ситуації

I j ( j 1,..., 5)

Одноцільова багатокритеріальна модель обґрунтування прийняття рішень у полі кількох інформаційних ситуацій

У практичній діяльності можливе поєднання інформаційних ситуацій.

Обґрунтування рішень у зазначених (а також інших) «проміжних» ситуаціях доцільно здійснювати за ієрархічною моделлю, наведеною на рис. 12, яка відображає ситуацію обґрунтування одноцільового багатокритеріального рішення у полі кількох інформаційних ситуацій.

55

На рисунку 12 використано умовні позначення, вже застосовані

~ — вектор-стовпчик рейтингів альтернативних рішень, отриманий

FF

у результаті зваженого згортання матриці FF за допомогою оператора KU ; ZF — оператор згортки функціонала оцінювання F у полі кількох

інформаційних ситуацій.

Рисунок 12 – Ієрархічна модель обґрунтування прийняття одно цільового багатокритеріального рішення у полі кількох інформаційних ситуацій

Багатоцільова багатокритеріальна модель обґрунтування прийняття рішень у полі кількох інформаційних ситуацій

Процес обґрунтування компромісу в полі кількох інформаційних ситуацій може розглядатися як ієрархічна модель (рис. 12), яка враховує можливість компромісу у полі кількох інформаційних ситуацій.

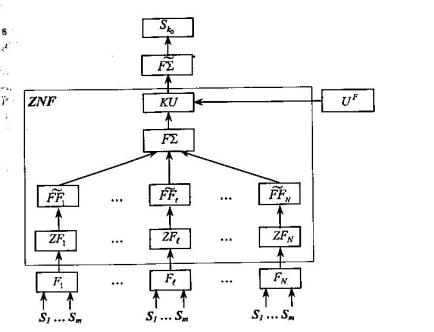
На рисунку 13 використано умовні позначення, застосовані на рисунках 12 та 11, а також:

F1 ,..., FN — функціонали оцінювання;

ZFl — оператор згортки функціонала оцінювання Fl , l 1,..., N ;

~

FFl — вектор-стовпчик, отриманий у результаті згортки функціонала оцінювання Fl , l 1,..., N ;

56

Рисунок 13 – Ієрархічна модель обґрунтування прийняття багатоцільового багатокритеріального рішення

Приклад. Маємо l =2, X x1 ,..., x6 , 1 , 2 , 3 , F F , F1 , F2 та F3

задані у вигляді таких матриць:

Прийняття рішення здійснюється у полі п’ятої інформаційної ситуації. Суб’єкт керування задає пріоритет з такими ваговими коефіцієнтами: u1 0.35 ; u2 0.65 .

57

Нормалізація – природна нормалізація. Критерій прийняття рішення

– критерій Вальда. Обирається показовий принцип врахування пріоритетів. Розв’язання. Для природної нормалізації для матриці F1 маємо:

– для стану середовища 1 :

Звідси одержимо

Для природної нормалізації для матриці F2 маємо:

– для стану середовища 1 :

тобто

58

Застосовуючи рівномірний вид згортки отримаємо матрицю функціоналу оцінювання:

За критерієм Вальда приймається оптимальне рішення x* x3 .

1.6Динамічні багатокритеріальні задачі

1.6.1 Поняття динамічного програмування [5-7, 11]

Динамічне програмування – це багатоетапний (багатокроковий) процес, на кожному етапі якого визначаються рішення деякої частини задачі, що обумовлено вихідною задачею.

Постановка задачі. Розглядається фізична система S, що перебуває у деякому початковому стані S0 S0 і являється керованою. За допомогою здійснення деякого управління U зазначена система переходить із

початкового стану S0 у кінцевий стан Sкон SR . При цьому якість

кожного з реалізованих управлінь U характеризується відповідним значенням функції W(U). Задача полягає у тому, щоб з безлічі можливих керувань U знайти таке U*, при якому функція W(U) набуває екстремального (мінімум або максимум) значення W(U*) (рис. 16).

Стан системи характеризується деякою точкою S на площині х10х2. Управління – це траєкторія руху. Задача полягає в тому, щоб із всіх припустимих траєкторій руху точки S знайти таку, котра вийде в результаті реалізації управління U*, що забезпечує екстремальне значення функції W(U*).

59