konspect_2010

1.2Експертні методи суб'єктивних оцінок у вимірі ризику

1.2.1 Поняття експертних методів [11, 4, 5-6]

Упрактичних задачах прийняття рішення альтернативи не являються математичними об’єктами, а найчастіше являють собою певні фізичні системи. Тому отримання опису альтернатив вимагає розробки методів рішення наступних задач: побудова множин можливих та припустимих альтернатив, формування набору аспектів, які є суттєвими для оцінки альтернатив, критерійного простору, впорядкування альтернатив за аспектами, отримання оцінок за критеріями чи відображення в критерійному просторі. Ці задачі являються модифікаціями задачі оцінювання, сутність якої полягає у зіставленні кількості чи декількох чисел системи, що розглядається. Методи розв’язку задач оцінювання засновані на використанні експертних процедур.

Експертні методи оцінки – це встановлення логічного об'єктивно існуючого зв'язку між об'єктами на основі думки незалежних експертів і наступною статистичною обробкою даної думки [17, 24, 26].

Задачі оцінювання виникають на різних етапах прийняття рішення. Вони можуть бути вирішені безпосередньо ОПР чи за допомогою консультантів (дослідників), коли оцінювання зводиться до вимірювання, до отримання довідкових даних та інших порівняно простих операцій.

Узагальному випадку у зв’язку зі складністю систем, які оцінюються, та складністю отримання інформації для вирішення задачі оцінювання залучаються особи, котрі володіють спеціальними знаннями та досвідом роботи з даною системою. Їх називають експертами, а рішення задачі оцінювання – експертизою.

1.2.2 Загальна схема експертизи [11]

Аналіз існуючих експертиз свідчить, що протягом процесу їх побудови можна виділити наступну послідовність дій:

1Дослідник знаходить множину припустимих оцінок , де міститься шукана оцінка.

2Дослідник визначає множину припустимих оцінок e , з якого

здійснюється вибір експертів.

3 Кожний експерт вибирає власну оцінку i Ci ( e ) e (i 1, N ) , тобто вирішує задачу вибору найкращої оцінки з e . При цьому експерти можуть взаємодіяти між собою.

10

4За розробленим алгоритмом дослідник виконує обробку отриманої від експертів інформації та знаходить результуючу оцінку з , яка являється розв’язком вихідної задачі оцінювання.

5Якщо отриманий результат не задовольняє дослідника, він може надати експертам додаткову інформацію, тобто організувати зворотній зв’язок, після чого він знову вирішує відповідні задачі вибору.

Обробка

Оцінка (C1 ( e ),..., CN ( e ))

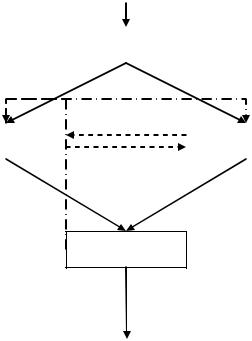
Рисунок 1– Блок-схема експертизи

Зазначена послідовність дій подана блок-схемою експертизи (рис. 1). Її параметри:

Ω– вихідна множина припустимих оцінок (МПО);

e – МПО для експертів;

L – взаємодія між експертами;

Q– зворотній зв’язок;

– обробка (відображення eN ).

Схема експертизи – п’ять параметрів, які зображені на блок-схемі. Підготовка експертизи – попередня розробка схеми експертизи та вибір експертів. Реалізація експертизи – отримання від експертів інформації та її обробка.

Іноді відображення представляється у вигляді:

11

де Ci – функція вибору i -го експерта (i 1, N ) ;

– композиція функцій вибору Ci та відображення q : e . Це означає, що спочатку знаходиться оцінка експертів з e , а потім за нею знаходиться результуюча оцінка з (рис.2).

C1 ( e )... CN ( e )

Обробка

Композиція q : e

Оцінка

Рисунок 2 – Блок-схема експертизи

1.2.3 Формування множини припустимих оцінок

Множина припустимих оцінок визначається задачею оцінювання,

полягає у впорядкуванні об’єктів, які утворюють систему, за зменшенням (збільшенням) значень деякої ознаки. При цьому

де i j – номер j -го об’єкта при вказаному впорядкуванні.

12

1.2.4 Характеристика групи експертів [11, 4-6]

Першим кроком при підборі експертів являється визначення кількісного складу експертної групи. Для кожної задачі це питання вирішується, як правило, окремо. Кількість експертів повинна буди достатньо великою для того, щоб вони в сукупності мали змогу врахувати суттєві властивості задачі та щоб рішення, знайдене за їх допомогою, було достатньо точним. При надто великій кількості експертів їх думки стають непогодженими (за рахунок експертів низької кваліфікації), виникають труднощі щодо організації процедури. З врахуванням цього доцільно включити до групи від 10 до 20 осіб. Можливі відхилення як до збільшення, так і до зменшення [11].

Коли чисельність експертної групи визначена, переходять безпосередньо до підбору експертів. Для цього визначають коло задач, які необхідно вирішити, та складають перелік осіб, котрі компетентні в даних областях.

Необхідні умови (характеристики) підбору експертів:

1 Компетентність, тобто ступінь кваліфікації експерта в певній галузі знань. Визначається на основі аналізу діяльності фахівця, рівня й широти ознайомлення фахівця з передовими технологіями, розуміння перспективного розвитку.

Кількісною оцінкою рівня компетентності є коефіцієнт компетентності, що розраховується за результатами висловлень фахівців про склад експертної групи. За даними висловленнями формується

j 1 i 1

13

i 1

де n – кількість експертів;

K i – коефіцієнт компетентності.

2Креативність – здатність до рішення творчих завдань. В основному, є тільки якісні визначення.

3Конформізм – врахування впливу пріоритетів. Чим вище ступінь конформізму, тим нижче власна оцінка проблеми.

4Відношення до експертизи (сумлінність, чесність).

5Конструктивність мислення, тобто пропозиції повинні бути із практичною спрямованістю й з урахуванням реальних можливостей.

6Колективізм – створення позитивного психологічного клімату.

7Самокритичність.

Кількісна оцінка правильності висловлення експертів може бути розрахована на основі визначення ваг i : вагові коефіцієнти виражають

ступінь компетентності. Нехай група експертів використовувалася багаторазово для оцінювання числових величин. Відносна помилка i -го експерта в j -й експертизі дорівнює

1.2.5 Статистичні методи обробки експертної інформації [11]

Результати оцінок кожного з експертів можна розглядати як реалізації деякої випадкової величини, яка набуває значення з e , та

застосовувати до них методи математичної статистики.

14

Статистичні методи дозволяють визначити погодженість думок експертів, значущість отриманих оцінок тощо. Ступінь погодженості вказує на якість результуючої оцінки.

Чисельні оцінки

Задача полягає у співвідношенні системі оцінки одного числа. Для її рішення використовується експертиза Е1:

E1 ;

e E1 ;

L – експерти ізольовані;

Q – зворотній зв’язок відсутній;

Ступенем погодженості думок експертів в експертизі Е1 є дисперсія 2 :

i

i 1

де i – оцінка i -го експерта;

a – результуюча оцінка.

Експертиза Е2, яка являється модифікацією експертизи Е1 для підвищення точності оцінювання, характеризується параметрами:

i 1

Інші параметри ті ж, що і в експертизі Е1. Ступінь погодженості методу оцінками визначається виразом

15

4 – ступінь невпевненості експерта у власній відповіді.

Векспертизі Е2 a1i , a2i , a3i інтерпретуються як оптимістична, найбільш

ймовірна та песимістична оцінки i -го експерта відповідно. Коефіцієнти1 , 2 , 3 , 4 визначаються емпірично. За однією методикою 1 1, 2 4 ,

3 1, 4 36 , за іншою 1 3 , 2 0 , 3 2 , 4 25 ( за другою методикою

1 3 , так як там вважається, що особа схильна занижувати оцінки).

Векспертизах Е1 та Е2 можна визначити статистичну значущість отриманих результатів. Маючи ймовірність помилки Pпом , вказується

інтервал, в який величина оцінки потрапляє з ймовірністю 1 Рпом :

вважається що величина a розподілена нормально з центром a та дисперсією (13). Тоді t / N , де величина t має розподіл Стьюдента з N 1 ступенів вільності. Її визначають за таблицями Стьюдента, маючи величину Pпом .

Приклад 1. Десять експертів з однаковими ваговими коефіцієнтамиi 1(i 1,10) оцінюють величину T . Від них отримані наступні оцінки:

T1 20,T2 24,T3 22,T4 37, T5 40,T6 35,T7 28,T8 31,T9 21,T10 25,5.

Значення T (за формулою 10) дорівнює 28,35. Дисперсія (за формулою 11) дорівнює 45,3; 6,73.

Маючи ймовірність помилки Pпом 0,05 , за таблицями розподілу Стьюдента визначаємо величину t : ступенів вільності 9; t 2,262 , 4,8 .

Таким чином, оцінювана величина з ймовірністю 0,95 знаходиться в інтервалі [23,5; 33,2].

Використання методу Дельфі для чисельної оцінки у вигляді

експертизи Е3 має вигляд:

обґрунтування оцінок, які виходять за даний діапазон.

16

Відображення задається наступним чином: увесь інтервал припустимих значень величини, яка оцінюється, ділиться на k інтервалів t1 ,..., tk ; експерт оцінює ймовірність знаходження величини, яка оцінюється,

в кожному з інтервалів; за результатами їх оцінок складається табл. 6, де pij – оцінка ймовірності знаходження величини, яка оцінюється в j -му

інтервалі, що надана i -м експертом.

На основі даної таблиці визначається думка експертів про знаходження величини, яка оцінюється, у кожному з інтервалів t j :

Результуючою оцінкою (C1 ( e ),..., CN ( e )) являється медіана отриманого розподілу q2 , що визначається з умови:

процедуру можна зупиняти, коли діапазон квантилів зменшується у 1,6 рази у порівнянні з попереднім.

Ранжирування

Жорстке ранжирування. Задача полягає у зіставленні системі, яка оцінюється, однієї перестанови. Визначимо експертизу Е4:

– множина всіх перестанов;

e ;

L – експерти ізольовані;

17

Q – зворотній зв’язок відсутній.

Відображення задається наступним чином: результати опитування експертів зводяться до таблиці 2.

У i -му рядку стоять ранги, які надані i -м експертом об’єктам ранжирування. У ( N 1)-му рядку знаходяться суми рангів за всіма експертами для певного об’єкта. Усі n об’єктів впорядковані у відповідності до величини rs , яка визначається за формулою

На перше місце ставиться об’єкт, у якого rs мінімальне, і так далі.

Степінь погодженості думок експертів визначається за допомогою коефіцієнта конкордації W .

Розглянемо два випадки: ранжирування всіх експертів співпадають, коли кожний об’єкт отримав від всіх експертів однаковий ранг, який для j -го об’єкту складає rj / N ; та другий – повна непогодженість експертів,

тобто протилежність оцінок ранжирування, які надаються експертами. Виходячи з (19) маємо

Сума рангів, які надаються кожним експертом (тобто вираз у дужках

n

у (20)), завжди дорівнює n(n 1) / 2 . Тому ri Nn(n 1) / 2 . За середній ранг

i 1

приймають величину

i 1

18

а за степінь погодженості думок – суму квадратів відхилень ri від середнього значення ri sr .

Коефіцієнтом конкордації W для випадку жорсткого ранжирування, тобто відсутності рівних рангів при ранжируванні кожного експерта, називається величина

де n – кількість об’єктів, N – кількість експертів.

Приклад 2. Нехай проводиться експертиза оцінки технологічного процесу. Існує перелік з шести ознак, які впливають на процес, десять експертів здійснювали ранжирування цих ознак за важливістю. Результати їх роботи наведені в табл. 3. Розрахуємо коефіцієнт конкордації. Суми

Нежорстке ранжирування. Задача полягає у зіставленні системі нежорсткого ранжирування (вектору з певними властивостями). При цьому деякі об’єкти можуть бути рівноцінними. Їм приписуються рівні ранги. Так, якщо об’єкти ділять місця 4-5, то кожний з них отримує ранг 4,5.

Експертиза Е5 для нежорсткого ранжирування відрізняється від експертизи Е4 тільки множиною .

Коефіцієнт конкордації для нежорсткого ранжирування

визначається формулою

i 1 j 1

19