
konspect_2010
.pdfАналогічно розраховуються елементи матриці витрат щодо другого покупця – Б. Матриця витрат має вигляд:
|
|
1 |
2 |
|
F f (xk |
|
|
|
|
, j ) x1 |
80 |
1000 |
. |
|
|
|
320 |
700 |
|
|
x2 |
|
||
Якщо виробник приймає рішення в умовах одержання гарантованого |
||||
результату (критерій Вальда), то необхідно продукцію відправити другому
покупцеві: |
|
min max f min 1000;700 700 тис.грн. |
||
~ |
|
|||
f |
||||
ko |
xk X j |
k |
xk X |
|
|
|
|
||
Якщо виробник приймає рішення, використовуючи апріорну інформацію відносно p( 2 ) =0,2, то, використовуючи критерій Байеса, продукцію необхідно відправити першому покупцеві:
~ |
|
n |
~ |
min 80 0.8 1000 |
|
700 0.2 min 264;396 264 |
fko min fkj p j |
0.2;320 0.8 |
|||||
xk X |
j 1 |
|
xk X |
|
xk X |
|
|
|
|
|
|
|
|
тис.грн. |
|
|
|
|
|
|
Тому |
що |
рішення виробника |
повинне |
залежати від результату |
||
експерименту, то необхідно використовувати апостеріорні імовірності. З огляду на, що деталі можуть вибиратися як з якісної партії, так і з бракованої, то визначені умовні імовірності p( v / j ) .
Апостеріорні імовірності знаходяться по формулі:
p( |
|
/ |
|
) |
p( j , v ) |
|
p( v / j ) p( j ) |
, |
|
j |
v |
p( v ) |
n |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
p( v / j ) p( j ) |
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
j 1 |
|
|
n |
|
|
|
n |
|
|
|
||
де p( v / j ) p( j ) |
p( j , v ) p( v ) – імовірність кожного окремого |
||||||||
j 1 |
|
|
|
j 1 |
|
|
|
||
результату експерименту; |
|
|
|
|
|
|
|||
p( v / j ) – умовні імовірності; p( j ) – апріорні імовірності; p( j , v ) – загальні імовірності.
Умовні імовірності визначаються на основі використання біноміального закону розподілу й умов проведення експерименту:
P(n, k) Cnk pk qn k ;q 1 p;k 0..n;Cnk |
n! |
, |
||
|
|
|||
k!(n k)! |
||||
|
|
|||
де n – обсяг вибірки.
Умовні імовірності в залежності від якості партії деталей для вибірки з двох деталей складуть:
p( |
/ ) C2 |
(0.96)2 |
(0.04)0 |
0.922; |
p( |
2 |
/ ) C1 |
(0.96)1 (0.04)1 |
0.0768; |
||
1 |
1 |
2 |
|
|
|
|
1 |
2 |
|
|
|
p( |
3 |
/ ) C0 |
(0.96)0 (0.04)2 0.0016; |
p( |
/ |
2 |
) C2 |
(0.85)2 |
(0.15)0 |
0.7225; |
|
|
1 |
2 |
|
1 |
|
2 |
|
|
|
||
|
|
|
|
p( 2 / 2 ) 0.255; |
p( 3 / 2 ) 0.0225 . |
|
|
||||
110
Таблиця 30 |
– Умовні ймовірності p( v |
/ j ) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
|
|
|
|
1 |
|
0,922 |
|
0,0768 |
0,0016 |
|
||
|
|
|
2 |
|
0,7225 |
|
0,255 |
0,0225 |
|
||
Таблиця 31 |
– Загальні ймовірності p( j , v ) |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
2 |
|
3 |
||
|
|
1 |
|
0,73760 |
|
0,06144 |
|
0,00128 |
|||
|
|
2 |
|
0,14450 |
|
0,05100 |
|
0,00450 |
|||
Визначаємо імовірності кожного результату експерименту:
p( 1 ) 0.73760 0.14450 0.8821 ; |
p( 2 ) 0.11244 ; |
p( 3 ) 0.00578 . |
|||||
Таблиця 32 – Апостеріорні ймовірності p( j |
/ v ) |
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
0,83619 |
|
0,54642 |
0,22145 |
|
|
|
2 |
0,16381 |
|
0,45358 |
0,77855 |
|
|
Остаточний результат залежить від результатів контрольної перевірки. За критерієм Байеса загальна формула для розрахунку витрат має вигляд:
n
B (xk , p j / v ) M (xk / v ) f (xk , j ) p( j / v ), k 1..n;v 1..N; N 3 .
j 1
Ситуація 1. Результат експерименту показав, що два вироби якісні:
M (x1 / 1 ) 80 0.83619 1000 0.16381 230.7 тис. грн.. M (x2 / 1 ) 320 0.83619 700 0.16381 382.25 тис. грн..
Мінімум очікуваних витрат досягається при реалізації першої стратегії – відправити продукцію необхідно першому покупцеві.
Ситуація 2. Результат експерименту показав, що один виріб якісний:
M (x1 / 2 ) 80 0.54642 1000 0.45358 497.29 тис. грн..
M (x2 / 2 ) 492.46 тис. грн..
Мінімум очікуваних витрат досягається при реалізації другої стратегії – відправити продукцію необхідно другому покупцеві.
Ситуація 3. Результат експерименту показав, що два вироби браковані:
M (x1 / 3 ) 80 0.22145 1000 0.77855 796.266 тис. грн..
M (x2 / 3 ) 615.85 тис. грн..
Мінімум очікуваних витрат досягається при реалізації другої стратегії – відправити продукцію необхідно другому покупцеві.
111

Приклад програмної реалізації
Рисунок 23 – Прийняття рішень на основі апріорних ймовірностей
Рисунок 24 – Прийняття рішень на основі апостеріорних ймовірностей
112
2.4Лабораторна робота 4. Прийняття багатоцільових рішень
Завдання. Нехай суб'єкт керування має Q(Q 0) ситуацій прийняття |
|||
рішень X , , F 1 |
, X , , F 2 |
, X , , F Q , які відрізняються функціоналом |
|
оцінювання |
в |
заданій |
інформаційній ситуації I . Необхідно визначити |
оптимальне |
рішення для всіх Q ситуацій прийняття рішень одночасно. |
||
Використання основних факторів v, u, w прийняття багатоцільових рішень дозволяє одержати ситуацію прийняття рішень із одним скалярним функціоналом оцінювання для заданої інформаційної ситуації I і критерію прийняття рішень.
Задано безліч рішень органа керування – X x1 ..xk , безліч можливих ситуацій – 1 ,..., q , тип функціонала оцінювання й інформаційна
ситуація.
Визначити відповідно до вихідних даних (таблиця 33) оптимальне рішення. Функціонали оцінювання будуються таким чином, щоб не було ідентичного повторення матриць, використовуючи генератор випадкових чисел у межах заданого діапазону.
Використати при певному типі інформаційної ситуації:
1) |
I1 – критерій Байєса (при q =2 p1 0.45 ; при q =3 |
p2 0.25, p1 |
0.35 ; при q =4 p2 0.2, p1 0.25, p3 0.3 ); |
2)I 4 – критерій Лапласа;
3)I 5 – критерій Вальда;
4)I 6 – критерій Гурвиця ( 0.6 ).
Пріоритет задається студентом самостійно за допомогою відповідних вагових коефіцієнтів.
Побудувати програмний модуль для прийняття багатоцільових рішень, передбачити можливість введення вихідних даних користувачем, інформативність алгоритму, висновок за результатами оцінки альтернатив за критерієм.
Таблиця 33 - Вихідні дані
|
|
|
Метод |
|
|
Тип |
Елементи |
|
||
№ |
q l |
k |
Співвідношення |
Критерій |
функціоналів |
матриць |
|
|||
нормалізації |
оцінювання |
|
|
q |
I |
|||||
варіанта |
пріоритетів u |
згортки w |
|
|
||||||
|
|
v |
F (F ) |
|
f k |
|
||||
|
|
|
|
|
|
min |
|
max |
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
6 |
відносної |
лінійний |
гарантованого |
+ |
0 |
|
15 |
1 |
нормалізації |
результату |
|
||||||||
|
|
|
|
|
|
|
|
|
||
2 |
3 |
7 |
природної |
показовий |
домінуючого |
+ |
1 |
|
9 |
4 |
нормалізації |
результату |
|
||||||||
|
|
|
|
|
|
|
|
|
||
3 |
4 |
8 |
порівняльної |
лінійний |
рівномірності |
- |
0 |
|
6 |
5 |
нормалізації |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
5 |
Севіджа |
показовий |
сумарної |
+ |
0 |
|
14 |
6 |
ефективності |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
9 |
відносної |
лінійний |
рівномірності |
- |
0 |
|
12 |
5 |
нормалізації |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
113
Продовження табл. 33
|
|
|
Метод |
|
|
Тип |
Елементи |
|
||
№ |
q l |
k |
Співвідношення |
Критерій |
функціоналів |
матриць |
|
|||
нормалізації |
оцінювання |
|
|
q |
I |
|||||
варіанта |
пріоритетів u |
згортки w |
|
|
||||||
|
|
v |
|
|
f k |
|
||||
|
|
|
F (F ) |
|
|
|||||
|
|
|
|
|
|
min |
|
max |
|
|
|
|
|
|
|
|
|
|
|
||
6 |
4 |
6 |
природної |
показовий |
гарантованого |
- |
0 |
|
16 |
6 |
нормалізації |
результату |
|
||||||||
|
|
|
|
|
|
|
|
|
||
7 |
4 |
7 |
порівняльної |
лінійний |
домінуючого |
- |
1 |
|
9 |
4 |
нормалізації |
результату |
|
||||||||
|
|
|
|
|
|
|
|
|
||
8 |
3 |
7 |
Севіджа |
показовий |
рівномірності |
+ |
1 |
|
10 |
1 |
9 |
3 |
5 |
відносної |
лінійний |
сумарної |
+ |
1 |
|
15 |
1 |
нормалізації |
ефективності |
|
||||||||
|
|
|
|
|
|
|
|
|
||
10 |
2 |
6 |
природної |
показовий |
рівномірності |
+ |
0 |
|
13 |
4 |
нормалізації |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
11 |
3 |
6 |
порівняльної |
лінійний |
гарантованого |
- |
1 |
|
11 |
5 |
нормалізації |
результату |
|
||||||||
|
|
|
|
|
|
|
|
|
||
12 |
2 |
7 |
Севіджа |
показовий |
домінуючого |
+ |
1 |
|
12 |
5 |
результату |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
13 |
3 |
8 |
відносної |
лінійний |
сумарної |
- |
1 |
|
8 |
4 |
нормалізації |
ефективності |
|
||||||||
|
|
|
|
|
|
|
|
|
||
14 |
4 |
9 |
природної |
показовий |
сумарної |
+ |
1 |
|
7 |
6 |
нормалізації |
ефективності |
|
||||||||
|
|
|
|
|
|
|
|
|
||
15 |
4 |
9 |
порівняльної |
лінійний |
рівномірності |
- |
0 |
|
5 |
6 |
нормалізації |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
16 |
4 |
8 |
Севіджа |
показовий |
гарантованого |
+ |
0 |
|
6 |
6 |
результату |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
17 |
2 |
8 |
Севіджа |
лінійний |
домінуючого |
- |
0 |
|
7 |
1 |
результату |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
18 |
3 |
7 |
відносної |
показовий |
сумарної |
- |
0 |
|
8 |
1 |
нормалізації |
ефективності |
|
||||||||
|
|
|
|
|
|
|
|
|
||
19 |
3 |
7 |
природної |
лінійний |
сумарної |
- |
0 |
|
10 |
4 |
нормалізації |
ефективності |
|
||||||||
|
|
|
|
|
|
|
|
|
||
20 |
2 |
6 |
порівняльної |
показовий |
рівномірності |
+ |
1 |
|
7 |
5 |
нормалізації |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
21 |
2 |
6 |
Севіджа |
лінійний |
гарантованого |
+ |
1 |
|
8 |
6 |
результату |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
22 |
4 |
5 |
природної |
показовий |
домінуючого |
- |
1 |
|
9 |
6 |
нормалізації |
результату |
|
||||||||
|
|
|
|
|
|
|
|
|
||
23 |
3 |
5 |
порівняльної |
лінійний |
домінуючого |
- |
1 |
|
10 |
4 |
нормалізації |
результату |
|
||||||||
|
|
|
|
|
|
|
|
|
||
24 |
4 |
8 |
природної |
показовий |
сумарної |
+ |
1 |
|
10 |
5 |
нормалізації |
ефективності |
|
||||||||
|
|
|
|
|
|
|
|
|
||
25 |
2 |
6 |
відносної |
показовий |
рівномірності |
+ |
0 |
|
4 |
5 |
нормалізації |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
114
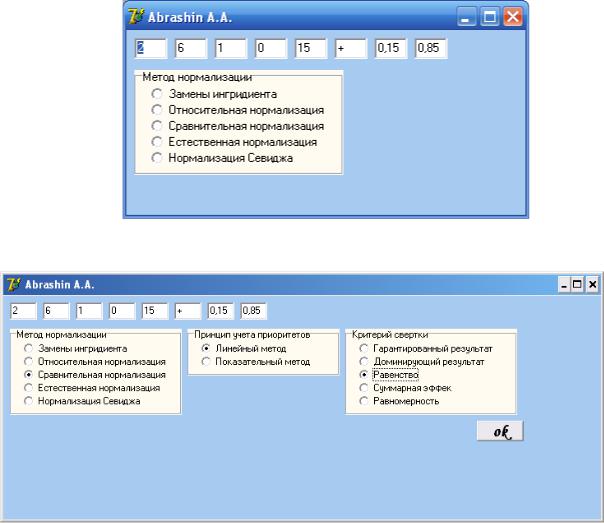
Приклад програмної реалізації
Рисунок 25 – Вихідні дані
Рисунок 26 – Вибір основних параметрів
115

Рисунок 27 – Нормалізація
Рисунок 28 – Врахування пріоритетів
116
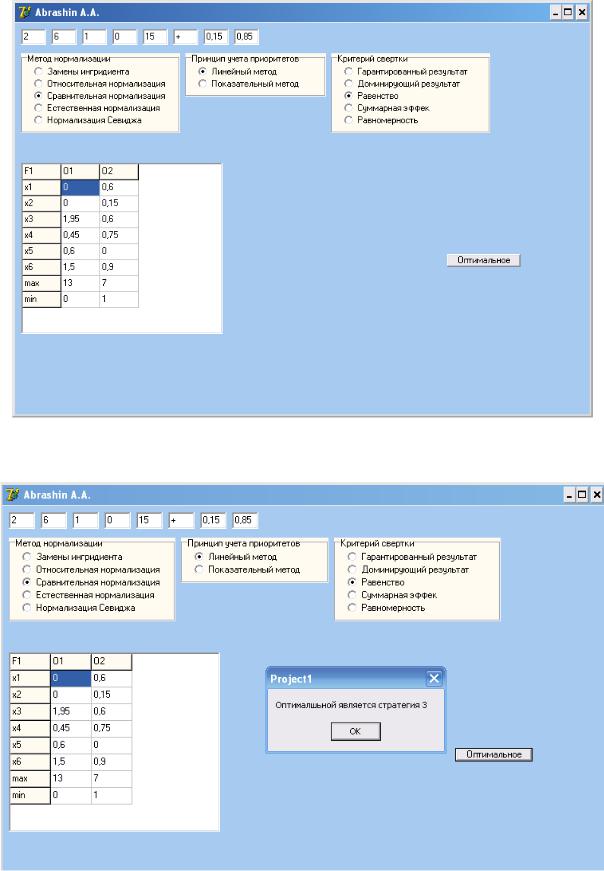
Рисунок 29 – Згортка
Рисунок 30 – Вибір оптимальної стратегії
117
2.5 Лабораторна робота 5. Прийняття рішень на основі методу динамічного програмування
Завдання. Знайти варіант розподілу капітальних вкладень між підрозділами на механізацію виробничих процесів, при якому буде забезпечене максимальне зниження трудомісткості обробки навантаження. Залежність між сумою виділюваних капітальних вкладень і зниженням трудомісткості обробки навантаження на кожному підрозділі представлена в таблиці 34 (В – номер у списку групи; границі заданих інтервалів використаються для заповнення матриці випадковим образом).
Побудувати програмний модуль для прийняття рішень, передбачити можливість введення вихідних даних користувачем, інформативність алгоритму, висновок за результатами.
Таблиця 34 - Вихідні дані
Обсяг капіталовкладень, |
Економія трудомісткості навантаження залежно від обсягу |
|||
тис. грн. |
|
капіталовкладень, чіл.-ч. |
|
|
|
підрозділ 1 |
підрозділ 2 |
підрозділ 3 |
підрозділ 4 |
0 |
В |
В |
В |
В |
В*10 |
[10; 20] |
[10; 20] |
[10; 20] |
[10; 20] |
2*В*10 |
[30; 40] |
[30; 40] |
[30; 40] |
[30; 40] |
3*В*10 |
[40; 50] |
[40; 50] |
[40; 50] |
[40; 50] |
4*В*10 |
[60; 70] |
[60; 70] |
[60; 70] |
[60; 70] |
5*В*10 |
[75; 90] |
[75; 90] |
[75; 90] |
[75; 90] |
118
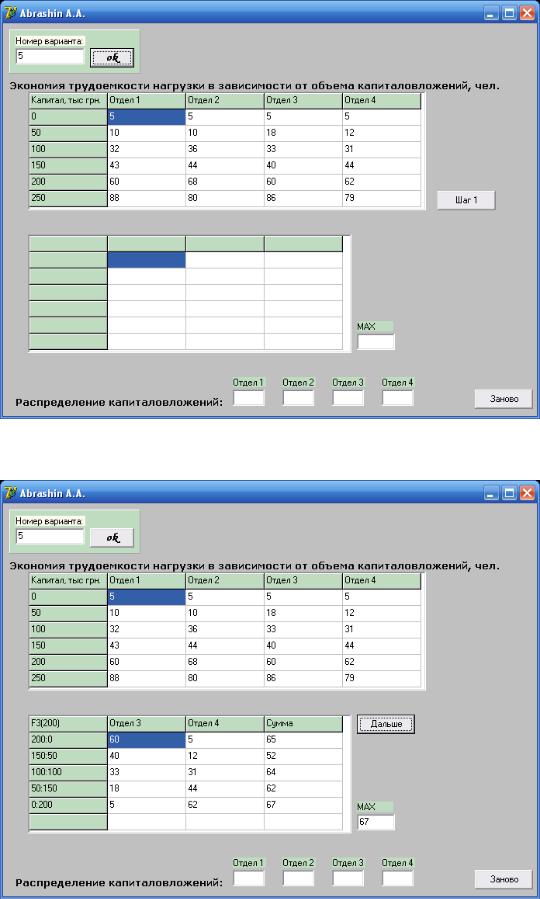
Приклад програмної реалізації
Рисунок 31 – Вихідні дані
Рисунок 32 – Етап 3-й методу динамічного програмування
119
