
kont_rus
.pdf
где n — отношение числа витков соленоида к его длине;
V — объем соленоида.
Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
а) при замыкании цепи:
I= E (1 − e− Rt L ),
L ),
R
где E — ЭДС источника тока;
t — время, прошедшее после замыкания цепи;
б) при размыкании цепи:
I = I0e− Rt L ,
L ,
сила тока в цепи при t=0;
t — время, прошедшее с момента размыкания цепи.
Энергия магнитного поля
W = LI 2 . 2
Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему):
w = BH  2 , или w = B 2
2 , или w = B 2  (2μμ0 ), или w = μμ0 H 2
(2μμ0 ), или w = μμ0 H 2  2 ,
2 ,
где В — магнитная индукция;
Н — напряженность магнитного поля.
111

|
|
Примеры решения задач |
|
|
|
|
||
Пример 4.1. По двум параллельным, прямым проводам длиной |
||||||||
l = 2,5 м каждый, находящимся на расстоянии d = 20 см друг от друга, текут |
||||||||
|
I1 |
I2 |
одинаковые |
токи |
I=1 |
кА. |
||
|
|
|
|
|
|
F |
||
|
|
|
Вычислить |
|
силу |
|||
|
|
dF |
взаимодействия токов. |
|
||||
|
|
1,2 |
|
|||||
|
dF1,2 |
|
Решение. |
Взаимодействие |
||||
|
|
dl |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
двух проводников, по которым |
|||||
|
|
|
текут |
токи, |
|
осуществляется |
||
|
|
|
через магнитное поле. Каждый |
|||||
Рисунок 17 |
|
ток создает |
магнитное |
поле, |
||||
|
|
|
которое |
действует |
на другой |
|||
проводник. Предположим, что оба тока (обозначим их I1 и I2) текут в |
||||||||
одном направлении. |
|
|
|
|
|
|
|
|
Вычислим силу F1,2, с которой магнитное поле, созданное током I1, |
||||||||
действует на проводник с током I2. Для этого проведем магнитную |
||||||||
силовую линию так (штриховая линия на рис. 17), чтобы она касалась |
||||||||
проводника с током I2. По касательной к силовой линии проведем вектор |
||||||||
магнитной индукции B1. Модуль магнитной индукции B1 определяется |
||||||||
соотношением |
(длинный |
проводник |
( l >> d ) |
можно |
приближенно |
|||
рассматривать как бесконечно длинный): |
|
|
|
|
|
|
||
B1 = |
μ0 I1 |
|
2πd . |
(58) |
Согласно закону Ампера, на каждый элемент второго проводника с
током I2 длиной dl2 в магнитном поле действует сила
dF |
= I B dl sin(dl , B ). |
||||
1,2 |
2 |
1 |
2 |
2 |
1 |
Так как отрезок dl перпендикулярен вектору В1, то sin(dl, B1 ) = 1, и
тогда
112

dF1,2 = I2 B1dl2 . |
(59) |
Подставив в выражение (59) B1 из формулы (58), получим
dF = μ0 I1I2 dl. |
|
1,2 |
2πd |
|
|
Силу F1,2 взаимодействия проводников с током найдем |
|
интегрированием по всей длине второго проводника. Также учтем, что, по третьему закону Ньютона, сила, действующая на первый проводник со стороны второго, будет равна найденной по модулю и противоположна ей по направлению:
|
μ 0 I1 I |
|
l2 |
|
μ 0 I1 I 2 |
|
F = |
2 |
∫ |
dl = |
l . |
||
2πd |
|
2πd |
||||
1, 2 |
|
2 |
2 |
|||
|
|
|
|
|||
|
|
|
0 |
|
|
|
Заметив, что I1=I2=I и l2 = l , получим
F1,2 = |
μ0 I 2l |
. |
|
|
2πd |
Убедимся в том, что правая часть этого равенства дает единицу силы (Н):
[μ0 ][I 2 ][l] = 1Гн/ м×(1А)2 ×1м = 1Дж =1Н.
[d ] |
1м |
1м |
Произведем вычисления:
F |
= |
4π ×10−7 × (103 ) 2 |
× 2,5 |
H = 2,5H . |
|
2π × 0,2 |
|
|
|||
1,2 |
|
|
|
|
|
|
|
|
|
|
|
Сила F1,2 сонаправлена с силой dF1,2 |
и определяется (в данном случае |
||||
это проще) правилом левой руки.
113
Ответ: F=2,5 H.
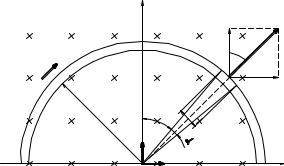
Пример 4.2. Провод в виде тонкого полукольца радиусом R=10 см
находится в однородном магнитном поле (B=50 мТл). По проводу течет ток I=10 А. Найти силу F, действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие
провода находятся вне поля.
Решение. Расположим провод в плоскости чертежа
перпендикулярно линиям магнитной индукции (рис. 18) и выделим на нем
малый элемент dl |
с током. На этот элемент тока Idl |
по закону Ампера |
будет действовать |
сила dF = I[dl B] . Направление |
этой силы можно |
определить по правилу векторного произведения или по правилу левой руки.
Используя симметрию, выберем координатные оси так, как это |
||||
изображено на рисунке. Силу dF представим в виде |
|
|||
|
R |
|
R |
|
|
dF = i dFx |
+ jdFy , |
|
|
где i и j — |
единичные векторы (орты); |
|
||
dFx и dFy — |
проекции вектора dF на координатные оси Ox и Оy. |
|||
|
Y |
|
|
|
|
|
|
jdFy |
dF |
|
|
|
|
|
|
I |
|
a |
|
|
|
|
|
|
|
|
|
idFx |
|
|
|
a |
d |
|
|
|
l |
|
|
|
j |
|
d |
|
|
|
|
|
|
|
0 |
i |
|
X |
|
Рисунок 18 |
|
||
Силу F, действующую на весь провод, найдем интегрированием:
R |
R |
R |
∫ dFx |
|
R |
∫ dF y , |
F |
= ∫ dF |
= i |
+ |
j |
||
|
L |
|
L |
|
|
L |
114

где символ L указывает на то, что интегрирование ведется по всей длине провода L.
Из соображений симметрии первый интеграл равен нулю (∫ dFx = 0).
|
|
L |
Тогда |
|
|
|
R |
|
F = |
j ∫ dFy . |
(60) |
|
L |
|
Из рис.11 следует, что |
|
|
dFy = dF ×cosα, |
|
|
где dF — модуль вектора dF . Так как вектор dl |
перпендикулярен |
|
вектору B , то dF = IBdl. Выразив длину дуги dl через радиус R и угол α ,
получим
|
dF = IBRdα . |
Тогда |
|
dFy |
= IBRcosα dα |
Введем dFy под интеграл соотношения (60) и проинтегрируем в |
|
пределах от − π / 2 до + π / 2 : |
|
|
+π / 2 |
F = jIBR |
∫cosα dα = 2 jIBR. |
|
−π / 2 |
Из полученного выражения видно, что сила F сонаправлена с положительным направлением оси Оу .
Найдем модуль силы F:
F = F = 2IBR.
115
Убедимся в том, что правая часть этого равенства дает единицу
силы (Н):
[I ][B][R] =1A ×1Тл×1м =1А× |
1Н ×1м |
|
×1м =1Н. |
|
|
||
1А×(1м) |
2 |
|
|
Произведем вычисления:
F = 2 ×10 ×50 ×10−3 × 0,1 = 0,1(H ).
Ответ: F = 0,1Н.
Пример 4.3. На проволочный виток радиусом r=10см, помещенный между полюсами магнита, действует максимальный механический момент
M max = 6,5 мкН. Сила тока I в витке равна 2А. Определить магнитную индукцию B поля между полюсами магнита. Действием магнитного поля Земли пренебречь.
Решение. Индукцию B магнитного поля можно определить из выражения механического момента, действующего на виток с током в магнитном поле,
M = pm Bsinα . |
(61) |
Если учесть, что максимальное значение механический момент принимает при α = π / 2 , а также что pm = IS , то формула (61) примет вид
M max = IBS.
Отсюда, учитывая, что S = πr 2 , находим |
|
B = M max /(πr 2 I ). |
(62) |
Произведя вычисления по формуле (62), найдем |
|
116
B=104 мкТл.
Ответ: B=104 мкТл.
Пример 4.4. Квадратная рамка со стороной длиной a = 2 см,
содержащая N = 100 витков тонкого провода, подвешена на упругой нити,
постоянная кручения C которой равна 10 мкН·м/град. Плоскость рамки совпадает с направлением линии индукции внешнего магнитного поля.
Определить индукцию внешнего магнитного поля, если при пропускании по рамке тока I=1 A она повернулась на угол α =60°.
Решение. Индукция B внешнего магнитного поля может быть найдена из условия равновесия рамки в магнитном поле. Рамка будет находиться в равновесии, если сумма механических моментов,
действующих на нее, будет равна нулю:
∑ M = 0. |
(63) |
В данном случае на рамку действуют два момента: M 1 — |
момент |
сил, с которым внешнее магнитное поле действует на рамку с током, и M 2
— момент упругих сил, возникающих при закручивании нити, на которой рамка подвешена. Следовательно, формула (63) может быть переписана в виде
M + M 2 = 0 .
Выразив М1 и М2 в этом равенстве через величины, от которых
зависят моменты сил, получим |
|
pm Bsinα −Cϕ = 0. |
(64) |
117

M2 |
I |



 I
I


 Pm
Pm 
 a
a 



 B
B
M1
Рисунок 19
Знак «мину» с перед моментом М2 ставится потому, что этот момент противоположен по направлению моменту М1.
Магнитный момент рамки с током определяется по формуле
pm = INS = Ia2 N,
где I — сила тока в рамке;
S =a2 — площадь рамки;
N — число витков рамки.
Тогда равенство (64) перепишем в виде
2 α − ϕ =
NIa Bsin C 0.
Откуда выразим магнитную индукцию внешнего поля:
B = |
Cϕ |
. |
(65) |
|
NIa2 sinα |
||||
|
|
|
Из рис. 19 видно, что α = π / 2 − ϕ , значит, sinα = cosϕ . С учетом этого равенство (65) примет вид:
B = |
Cϕ |
|
|
NIa 2 cosϕ . |
(66) |
||
|
118
Так как значение угла ϕ дано в градусах, то значение постоянной
кручения C, рассчитанной на градус, равно C =10 ×10−6 Í × ì / ãðàä .
Подставим данные в формулу (66) и произведем вычисления:
B = |
|
10 ×10 |
−6 × 60 |
= 0,03Òë = 30ìÒë . |
|
|
|
|
Òë |
||
|
×1× (0,02)2 ×1/ 2 |
||||
100 |
|
|
|||
Ответ: B=30мТл.
Пример 4.5. Плоский квадратный контур со стороной длиной
а=10 см, по которому течет ток I=100 А, свободно установился в
однородном магнитном поле индукцией B=1 Тл. Определить работу A,
совершаемую внешними силами при повороте контура относительно оси,
проходящей |
через |
середину |
его противоположных сторон, на |
угол: |
|
1) ϕ = 90O ; |
2) ϕ |
2 |
= 3O . При |
повороте контура сила тока в |
нем |
1 |
|
|
|
|
|
поддерживается неизменной. |
|
|
|||
Решение. На контур с током в магнитном поле действует |
|||||
механический момент |
|
|
|||
|
|
|
|
M = pm Bsinϕ . |
(67) |
По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (М=0), а
значит ϕ = 0 , т. е. векторы pm и В совпадают по направлению.
Если внешние силы выведут контур из положения равновесия, то возникший момент сил, определяемый формулой (67), будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный
(зависит от угла ϕ поворота), то для подсчета работы применим формулу работы в дифференциальной форме:
dA = Md ϕ. |
(68) |
119
Подставив сюда выражение M по формуле (67) и учтя, что
pm = IS = Ia2 ,
где I — сила тока в контуре;
S =a2 — площадь контура, получим:
dA= IBa2 sinϕ dϕ.
Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:
ϕ |
|
|
||||
A = IBa 2 ∫ sin ϕdϕ . |
|
(69) |
||||
0 |
|
|
|
|
|
|
1) Работа при повороте на угол ϕ = 90O : |
|
|
||||
1 |
|
|
|
|
|
|
π / 2 |
|
|
||||
A1 = IBa 2 ∫ sin ϕdϕ = IBa 2 |
|
- cos ϕ |
|
π0 |
/ 2 = IBa 2 . |
(70) |
|
|
|||||
|
|
|
||||
0 |
|
|
|
|
|
|
Убедимся в том, что правая часть этого равенства дает единицу работы (Дж):
[I ][B][a2 ] =1A×1Тл×(1м)2 =1Н ×1м =1Дж.
После вычисления по формуле (70) найдем:
A1=1 Дж.
2) Работа при повороте на угол ϕ2 = 3O . В этом случае, учитывая, что угол ϕ2 мал, заменим в выражении (69) sin ϕ на ϕ :
120
