66,Иерархический граф представляет собой четверку множеств. Каких?

Для описания электроавтоматики можно использовать формализм иерархических графов, который особенно удобен для графического описания автоматических циклов. Иерархический граф представляет собой «четверку» множеств:

• Простые вершины-состояния, изображаемые кружками, причем состояния могут быть статическими или динамическими. Выход со статического состояния инициируется извне, тогда как выход из динамического состояния происходит по завершению процесса.

• Сложные вершины-состояния, изображаемые двойными кружками (с двойным бордюром), причем такие состояния являются вложенными графами.

• Дуги, которые отражают переходы между состояниями любого типа.

• Узлы, которые разрезают дуги, изображаются темными кружками, причем узлы фиксируют условия изменения состояний любого типа. Если дуга выходит со статической вершины-состояния, то узел может одновременно принадлежать другому графу того же или другого уровня иерархии.

67,Из каких этапов состоит описание сложного цикла автомата?

Методика описания сложного цикла электроавтоматики включает в себе следующие этапы:

• разработка первичного автомата, т.е. автомата верхнего уровня иерархии, который является, в сущности, диспетчером режимов;

• разработка режима нерегулярных ситуаций (внутреннего режима), который сохраняет корректность состояния управляемого объекта при любых переключениях основных режимов, а также гарантирует неизменное состояние объекта, если цикл пассивный;

• выделение параллельно работающих автоматов, которые действуют в рамках цикла;

• разработка автоматов нижнего уровня иерархии.

68,Что представляет собой сеть Петри с точки зрения теории графов?

С точки зрения теории графов сеть Петри – это ориентированный граф с двумя типами вершин, соединяемых дугами.

Первый тип вершин называется местом или позицией и обозначается кружком, аналогично состоянию автомата на графе, второй тип вершин называется переходом и обозначается чертой, которая по смыслу обозначает барьер (рис.8.1).

Рисунок 8.1 – Графическое обозначение позиций и переходов

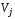
Место и переход могут иметь несколько входных и выходных дуг, однако дуги должны соединять только вершины разных типов, то есть позиции и переходы .

69,Как интерпретируются позиции, переходы и фишки сети Петри?

Если сеть Петри моделирует программу, то по отношению к программным действиям позиции, переходы и фишки интерпретируются следующим образом:

Переход моделирует операторы, а позиции хранят информацию об условиях свершения событий.

Когда двигающиеся по дугам фишки передвинутся в эту позицию, информация по выходящей из позиции дуге поступит на переход, в котором реализуется оператор, т.е. произойдет само событие.

Таким образом, функционирование сети можно трактовать как последовательность дискретных событий.

70,Какими множествами определяется сеть Петри?

Формально сеть N определяется пятеркой множеств:

,

где или – конечное непустое множество символов , называемых местами (позициями) сети;

или – конечное непустое множество символов , называемых переходами;

– функция инциндентности (табл. 8.1), указывающая на наличие дуг, соединяющих места с переходами , причем, если ,такая дуга есть, а если , такой дуги нет;

– функция инциндентности (табл. 8.2), указывающая на наличие дуг, соединяющих переходы 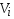с местами , причем, если , такая дуга есть, а если , такой дуги нет;

Таблица 8.1 – Функция инциндентности

	1	1	0
	0	0	1
	0	0	1
	0	1	0

_{Таблица 8.2 – Функция} инциндентности

	0	1	0	1
	0	0	1	0
	1	0	0	0

– начальная разметка сети Петри, представляющая собой множество мест во множестве целых положительных чисел {0, 1 ,2,…},которые указывают количество фишек на каждом месте.