Загальні вказівки
Алгоритм лінійної структури – це алгоритм, у якому блоки виконуються один за одним. Такий порядок виконання блоків називається природним.
Приклад 1. Обчислити y = 2cos2x, де x=2lna; a=6,7.
Блок-схема
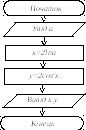
Порядок роботи:
Крок 1. Уводимо a.
Крок 2. Обчислюємо x = 2lna.
Крок 3. Обчислюємо y = 2cos2x.
Крок 4. Друкуємо x, y.
Крок 5. Останов.
Алгоритм структури, що розгалужується, – це алгоритм, у якому передбачене розгалуження виконуваної послідовності дій у залежності від результату перевірки якої-небудь умови.
Приклад 2. Обчислити корені квадратного рівняння
ax2 + bx + c = 0
за умови d = b2-4ac 0 за формулою
.
У противному випадку, тобто при d<0, передбачити вивід повідомлення «Дійсних коренів немає».
Блок-схема
Порядок роботи:
Крок 1. Уводимо a, b, c.
Крок 2. Обчислюємо d = b2 - 4ac.
Крок 3. Якщо d<0, виводимо повідомлення «Дійсних коренів немає», останов.
Крок 4. Обчислюємо
.
Крок 5. Виводимо x1, x2.
Крок 6. Останов.
Алгоритм циклічної структури – це алгоритм, у якому передбачене кількаразове виконання однієї і тієї ж послідовності дій, називаної циклом. Структура циклу: спочатку встановлюємо початкові значення всім змінним циклу, тобто визначаємо їхній стан до першого виконання операцій. Потім описуємо операції, виконувані багаторазово, тобто тіло циклу, далі робимо іншою змінну, визначаючу кількість повторів циклу, тобто параметр циклу. Завершується алгоритм умовою виходу з циклу.
Приклад 3. Знайти суму ряду
y =
,при
0
x
,
x =
/20.
Порядок роботи:
Крок 1. Установимо початкове значення суми s = 0.
Крок 2. Визначимо початкове значення параметра циклу x = 0.
Крок 3. Поки x , виконуємо кроки 3-7, інакше - йдемо на крок 8.
Крок 4. Обчислюємо y = sinx / (x2+1).
Крок 5. Обчислюємо суму s = s + y.
Крок 6. Збільшуємо значення x на крок: x = x + /20.
Крок 7. Повертаємося на крок 3.
Крок 8. Останов.
Приклад 4. Обчислити y = sin(3x)/x при 1 x 100 із кроком 0,5.
Б
лок-схема
Порядок роботи:
Крок 1. Задаємо початкове значення x=1.
Крок 2. Поки x 100, виконуємо кроки 3-6, інакше - крок 7.
Крок 3. Обчислюємо y = sin(3x)/x..
Крок 4. Виводимо x, y.
Крок 5. Збільшуємо значення x на крок: x = x + 0,5.
Крок 6. Повертаємося на крок 2.
Крок 7. Останов.
Завдання для самостійної роботи
Завдання 1. Намалювати блок-схему для обчислення h, узявши значення функцій з таблиці 2.
Таблиця 2
|
Вар. |
h |
a |
b |
с |
x |
|
1 |
a2+b2-6c |
x2-e-x |
lnx+ |
cos2x+x5 |
5,4 |
|
2 |
c2+8b+10a |
sin2x+x1/4 |
tgx-8x3 |
x4+2sinx2 |
1,2 |
|
3 |
3a2+4b-8 |
3x-2cos3x |
lnx+2ex |
x1/3+4x-1 |
0,3 |
|
4 |
a3+b2-8c |
sin3x+x4 |
|
4x-5x3 |
1,7 |
|
5 |
6b3+4c-2 |
tgx+e2x |
x2-6x3 |
1/x-2lnx |
4,1 |
|
6 |
a2+b2+c2 |
ex+e2x+4 |
x-sin3x |
x2/cos3x |
2,4 |
|
7 |
5b3-2a+c |
tgx-2x |
|
x3/7 |
5,5 |
|
8 |
4a2+5b2 |
cosx+2x |
x4-2x/5 |
2x-5 |
4,6 |
|
9 |
3ab-4c |
sin2x+5 |
cosx5 |
x1/3+tgx |
1,6 |
|
10 |
c2+5a3-b |
cos3x-6x |
-4x3+lnx |
e2x+4cosx |
4,6 |
|
11 |
2a+4c-b4 |
ex-2lnx |
2x-5/x |
x5-2lnx |
3,9 |
|
12 |
a2+b2+c2 |
2/x+x3 |
lnx2-4x |
tgx-sin2x |
4,1 |
|
13 |
(a+b)2 |
lnx+2ex |
tgx+e2x |
x2-e-x |
3,4 |
|
14 |
2ac-3cb |
1/x-2lnx |
cosx+2x |
sin2x+x1/4 |
1,9 |
|
15 |
5c+2a4 |
x2-2/x |
(2-x)/6 |
cos3x-2x |
2,3 |
|
16 |
a+b+c |
lnx/2x |
x3-4x |
tgx-2x |
4,2 |
|
17 |
2a+3b+4c |
x2+x3 |
lnx-x4 |
cos2(x-4) |
2,8 |
|
18 |
a2+b3+c4 |
sin2x+x1/4 |
x3+4x |
ex+2lnx |
1,3 |
|
19 |
a+2b+3c |
2x-x1/4 |
|
tgx-4x |
3,1 |
|
20 |
2(a+b)-c4 |
(x3-x/2)3 |
lnx-e2x |
|
2,4 |
|
21 |
c2-b3 |
2x+sinx4 |
sin(x-lnx) |
lnx2+2x |
1,1 |
|
22 |
3a-4cb |
2cosx3 |
tgx/4 |
x/5 |
3,1 |
|
23 |
c5-2ab |
½sin3x |
sin6x/x3 |
x-4sin2x |
1,8 |
|
24 |
6a+3b3+c |
cosxx+2x |
sin2x+tgx |
lnx-e-x |
2,1 |
|
25 |
4abc |
xx-sinx3 |
x/2-x5 |
2x-sin3x |
4,1 |
|
26 |
a2+(b-c)5/3 |
2x1/3+1 |
sin(x2+4) |
lncos3x |
5,3 |
|
27 |
(a+4b)1/3-c2 |
tg(2x)/4 |
cosx2/x1/5 |
e-2x+1/x2 |
3,8 |
|
28 |
a1/3+(b3-c) |
x+23x |
lnsin34x |
arcsin2x |
4,2 |
|
29 |
b3+(a-4c)1/5 |
53x/(3x-1) |
e-5x+4/x |
cos(x1/3) |
2,6 |
|
30 |
c1/5-(b+3a)2 |
|
cosx+x2 |
arctg(x3) |
1,3 |
-lnx
-sinx
-2cosx
+ex
Завдання 2. Намалювати блок-схему для обчислення
y = f(x), де
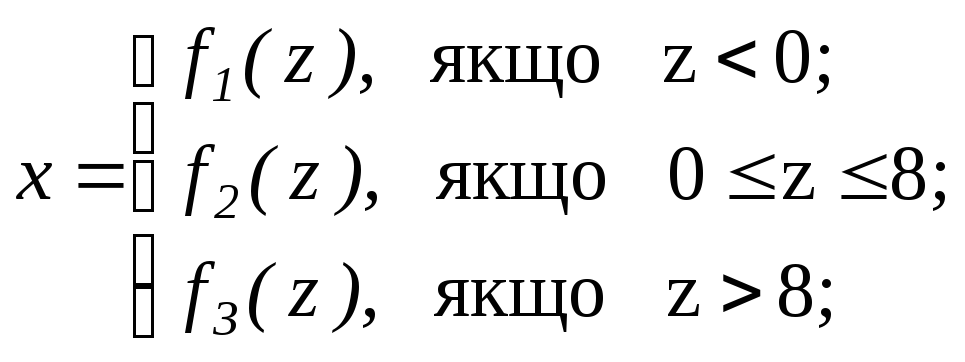
z = cos(с).
Значення функцій наведені в таблиці 3.
Таблиця 3
|
Вар. |
f(x) |
f1(z) |
f2(z) |
f3(z) |
c |
|
1 |
x2+8x-6 |
z3-3z2 |
zln(z) |
ez-e-z |
5,1 |
|
2 |
x3lnx2 |
e-z+3z |
ln|z| |
cosz+z2 |
5,4 |
|
3 |
x1/4+sinx |
2z-ln|z| |
tgz-2z |
sin3z |
4,1 |
|
4 |
x4+2sinx2 |
sinz+tgz |
cos3z+3/z |
z2+lnz2 |
3,2 |
|
5 |
cosx3 |
z2+2sinz |
lnz+2z |
ez+1/z |
4,7 |
|
6 |
sinx+2lnx |
2z+tgz |
lnz4+2z |
cosz+2z |
1,3 |
|
7 |
sin4x2 |
sinz2-z3 |
|
2sinz2 |
1,6 |
|
8 |
tgx-4x3 |
1/cos2z |
z-ln|z| |
z3+sinz |
1,5 |
|
9 |
lnx-e2x |
z2+ez |
cos4z/z3 |
tg(z+1/z) |
2,7 |
|
10 |
2x-lnx |
2cosz+1/z |
z3-2ln|z| |
tg2z+z3 |
3,8 |
|
11 |
3x-sinx |
3tg3z |
1/cos4z |
e2z+sinz |
1,6 |
|
12 |
4x2+cosx |
3z/sinz |
z2+2sinz |
2z-ln|z| |
2,4 |
|
13 |
|
z2+lnz2 |
ez+1/z |
z4-sinz |
4,1 |
|
14 |
x1/3+2x |
ln|cosz| |
2z+ez |
tg2z |
2,5 |
|
15 |
sin4x+2x |
z5/sin2z |
e-2z+tgz |
cos4z+z1/3 |
3,2 |
|
16 |
tg4x+1/x |
z/sinz1/5 |
2ztg3z |
z |
1,4 |
|
17 |
ln(1/x) |
zsin2z-8 |
lnsinz0,8 |
|
2,3 |
|
18 |
e2x+4x |
cos( /4)-z |
1/(ez+1) |
arctg(z+3) |
4,1 |
|
19 |
cosx4+x/2 |
sin(z+30 ) |
lncos(z/6) |
e-tg(z-2) |
3,2 |
|
20 |
2tgx+ex |
z+cos( +z) |
z3+z1/3 |
z4-lnz |
2,8 |
|
21 |
2lnx2 |
arccosz2 |
sinz+lncosz |
z3-sin( x) |
1,7 |
+cosx
+8
-2,5Продовження таблиці 3
|
Вар. |
f(x) |
f1(z) |
f2(z) |
f3(z) |
c |
|
22 |
cos2x/3 |
z2+ln(z+4) |
e(z-5)+sinz |
|
2,2 |
|
23 |
1/tgx4 |
e-4z+2+z2 |
cos(z1/3+2) |
sin( +4z2) |
5,6 |
|
24 |
e2x-x3 |
tg(z2+ |
ln(sinz+5) |
z4+z2-cosz |
3,4 |
|
25 |
tgx-2lnx |
arcsin(z+3) |
z3-z2+cosz |
ln(z3+4z) |
2,5 |
|
26 |
cosx4+x/2 |
lnsinz0,8 |
cos( /4)-z |
z/sinz1/5 |
3,7 |
|
27 |
ln(x+x2) |
2ztg3z |
sin( +4z2) |
z3+z1/3 |
2,6 |
|
28 |
cosx4+2x |
tg(z+1/z) |
e2z+sinz |
cosz1/5 |
3,8 |
|
29 |
sin4x+2x |
z2+lnz2 |
cos3z+3/z |
cos( /4)-z |
5,8 |
|
30 |
3ln(x2+5) |
z4-lnz |
sinz+tgz |
sinz+lncosz |
3,5 |
)
Завдання 3. Знайти суму ряду
y =
,де
a
x
b,
x = c.
Варіанти завдань наведені в таблиці 4.
Таблиця 4
|
Вар. |
f1 |
f2 |
a |
b |
c |
|
1 |
3x-1 |
e-1/x+x/(x+1) |
3 |
5 |
0,5 |
|
2 |
x3-3x2 |
x4+2x2+3 |
1 |
3 |
0,2 |
|
3 |
e-x+4x |
|
0,6 |
4,2 |
0,3 |
|
4 |
sin2(x+4x3) |
(x+2x3) |
0,5 |
4,8 |
0,2 |
|
5 |
xsinx3-ln2x |
arctgx/4+e-x+2 |
2 |
6,3 |
0,4 |
|
6 |
x4-cosx |
tgx+2x |
1 |
5 |
0,5 |
|
7 |
2x+sin2x |
|
5 |
8 |
0,3 |
|
8 |
ln(4x+8) |
e-x+sin2x |
1 |
4 |
0,2 |
|
9 |
x3ln(2x) |
4x2+6x3-2 |
0,5 |
6 |
0,3 |
|
10 |
x2+sin3x |
cos3x+e-2x |
-2 |
3 |
0,4 |
|
11 |
xe-x |
sin4x+x3 |
1,5 |
5 |
0,3 |
Продовження таблиці 4
|
Вар. |
f1 |
f2 |
a |
b |
c |
|
12 |
|
arctgx/5+2x |
0,6 |
4 |
0,2 |
|
13 |
x2/(3x+2) |
sin2( x+1) |
0,5 |
5,2 |
0,3 |
|
14 |
|
3x/(x-2) |
1,2 |
6,3 |
0,4 |
|
15 |
x3x+1+8x |
|x-8|+sinx |
4 |
7,5 |
0,3 |
|
16 |
x4+ex+3 |
xarctg(x/3) |
2 |
6,4 |
0,2 |
|
17 |
ln2(x+4) |
sin3(x/5) |
1 |
6,8 |
0,3 |
|
18 |
ex-2+x3 |
x-ln|x-1| |
0 |
4 |
0,4 |
|
19 |
2cos(x+3) |
4x2/(3+x3) |
2 |
5 |
0,3 |
|
20 |
|
tg2(x+4)-e-x |
1 |
6 |
0,4 |
|
21 |
3+2sin2(x-3) |
4+x/10 |
2 |
7 |
0,5 |
|
22 |
ln(1+2x) |
sin2(4x+1) |
1,5 |
6,8 |
0,4 |
|
23 |
|
5arctg(4x) |
2 |
7 |
0,5 |
|
24 |
arcsin(x+2) |
3(x-4)/(x2+1) |
3 |
8 |
0,2 |
|
25 |
e|x+2| |
ln2(x+4) |
-2 |
6 |
0,3 |
|
26 |
(4-x)cos2x |
|
1 |
7 |
0,4 |
|
27 |
|
sinx4-4 |
-2 |
5 |
0,2 |
|
28 |
2x+4+cos2x |
ln|x+8| |
-4 |
2 |
0,5 |
|
29 |
(x+2)/sin3x |
|
1 |
4 |
0,3 |
|
30 |
ex+3+4x2 |
arcsinx3 |
2 |
5 |
0,2 |
+e-x
+e-3x
