Кривые на плоскости

Общее уравнение кривых второго порядка – это многочлен вида:

Ax²+Bxy+Cy²+Dx+Ey+f=0

Окружность – геометрическое место точек, равноудаленных от заданной точки (центра).

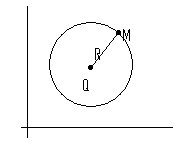
Каноническое уравнение окружности:

Эллипс – совокупность точек, сумма расстояний от которых до двух данных (фокусов) есть величина постоянная.

Эллипс имеет две оси симметрии – главные оси эллипса, и центр симметрии – центр эллипса.

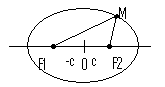
F₁M+F₂M=const

Если центр эллипса находится в т. С(), то каноническое уравнение имеет вид:

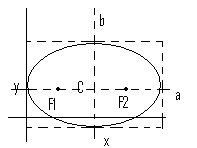
Построение эллипса по каноническому уравнению. С() – центр.

а – большая полуось, b – малая полуось (наоборот, если эллипс расположен вертикально)

- фокусное расстояние.

- коэффициент сжатия эллипса.

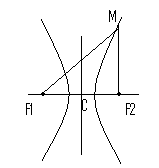
Гипербола – совокупность точек плоскости, разность расстояний которых до двух данных точек (фокусов) есть величина постоянная.

Аналогично прошлым преобразованиям получаем каноническое уравнение гиперболы:

Если центр гиперболы смещен в т. С()

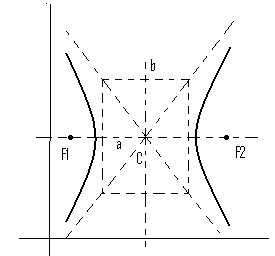
Построение гиперболы по каноническому уравнению:

Минус может стоять перед первым слагаемым, тогда гипербола меняет ориентацию, ее ветви растут вдоль оси у.

С(); а – действительная полуось; b – мнимая полуось.

- фокус расстояния.

Парабола – совокупность точек плоскости, равноудаленных от данной точки (фокуса) и данной прямой директрисы.

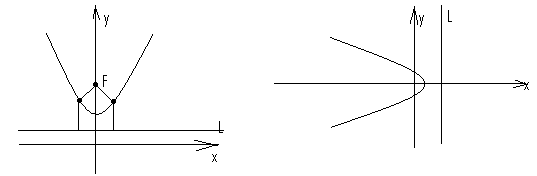
Если в уравнении перед 2р стоит «+», то рост ветвей осуществляется по направлению оси, если «-» - то против.

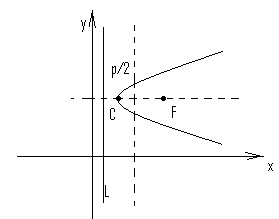
Построение параболы по каноническому уравнению:

; р – расстояние F до L

- вершина параболы

- равноудалены от вспомогательной оси.

Примечание:

А=В – окружность

- эллипс

- гипербола

А=0 или В=0 – парабола

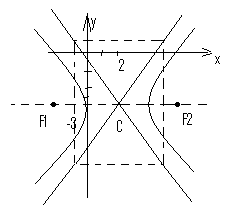
Пример:

Привидение квадратичной формы к каноническому виду и построение графика

Выделим полные квадраты

- каноническое уравнение

Плоскости в пространстве

Плоскость в пространстве характеризует нормальный вектор

;

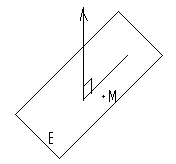
Ax+By+Cz+D=0 (1) общее уравнение плоскости

(2)

-уравнение плоскости, содержащей точку М(х₀;у₀; z₀). С нормальным вектором

Каноническое уравнение плоскости, где a,b,c-отрезки осей координат, которые отсекает плоскость

Уравнение плоскости, проходящей через 3 точки:

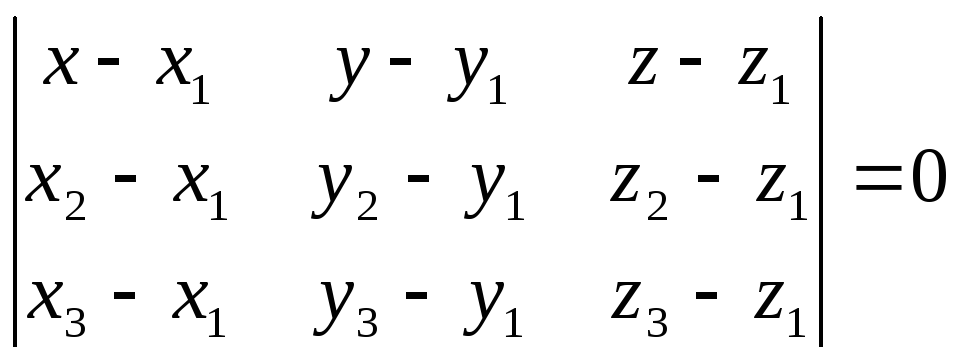(4)

Соотношения плоскостей:

1) ,

2)

3)

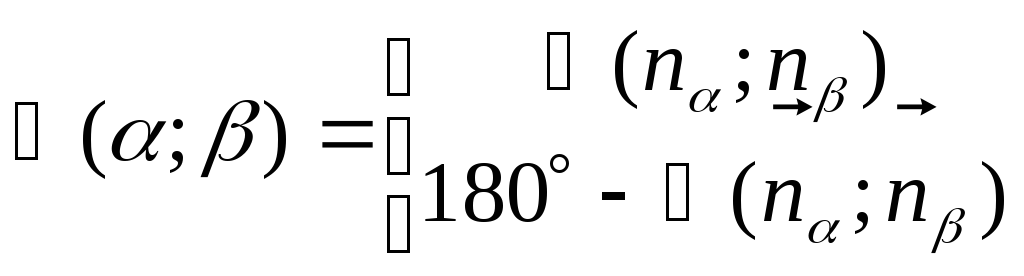
Прямые в пространстве

Общее уравнение прямой – линия пересечения двух плоскостей.

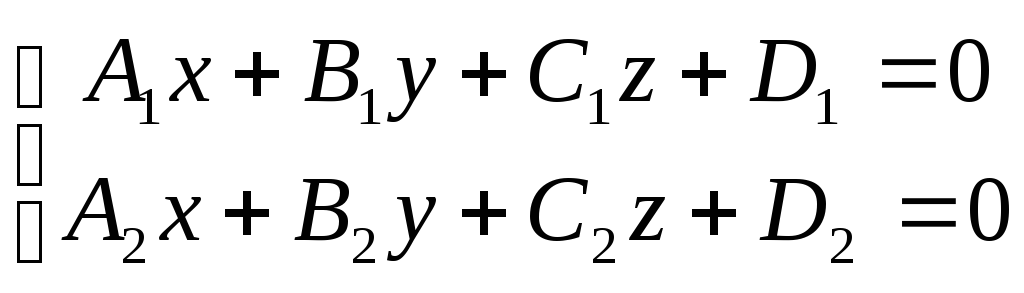
- направляющий вектор, т. ;. Уравнение прямой, проходящей через т.М с направляющим вектором :

Параметрическое уравнение:

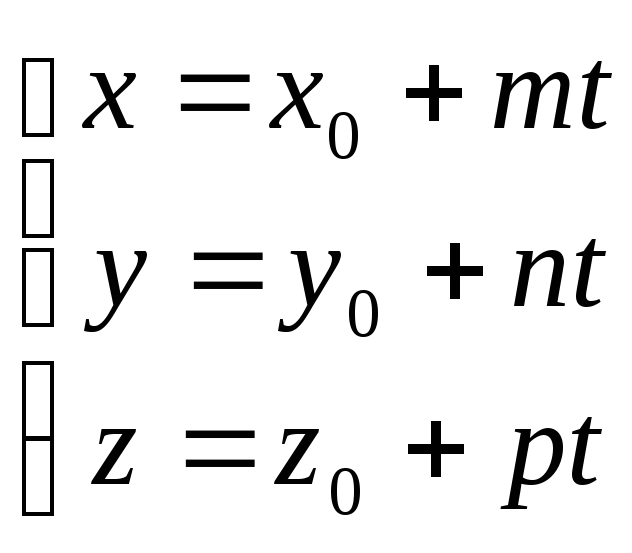
Уравнение прямой, проходящей через две точки:

Соотношения между прямыми:

1)

2)

b

3)

a

b

Соотношения между прямой и плоскостью:

1)

2)

3)

Нужно учитывать, что угол между прямой и плоскостью всегда острый.

Расстояние от т.М() до плоскости

Пример:

№1 Написать уравнение плоскости, проходящей через т.М(1;3;-1) и имеющий нормальный вектор

№2 Прямая задана как линия пересечения двух плоскостей. Написать ее каноническое уравнение

Ι способ. Найдем две точки, общие для плоскостей α иβ, и напишем уравнение прямой, проходящей через две точки.

Пусть х=0

Тогда , т.М()

Пусть у=0

Тогда , т.N()

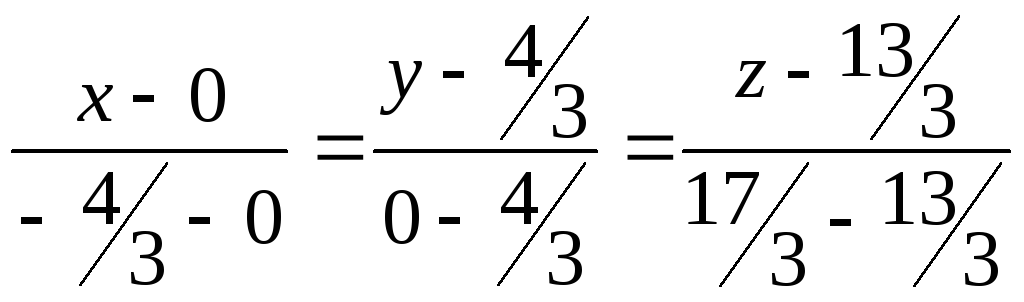
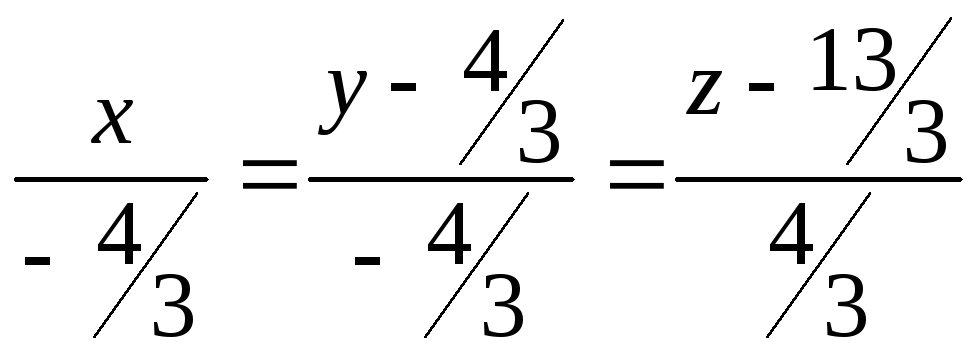
ΙΙ способ. Воспользуемся т. М из предыдущего решения и найдем вектор, который перпендикулярный сразу двум нормальным векторам – направляющий для линии пересечения.

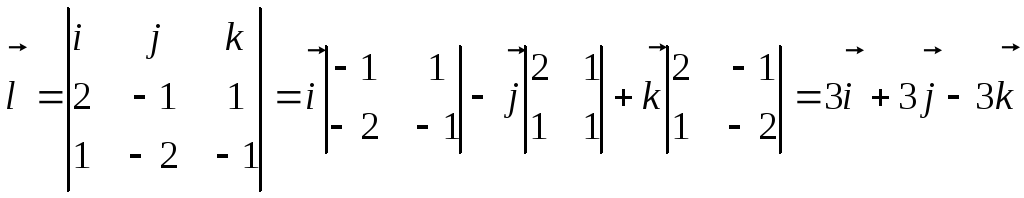
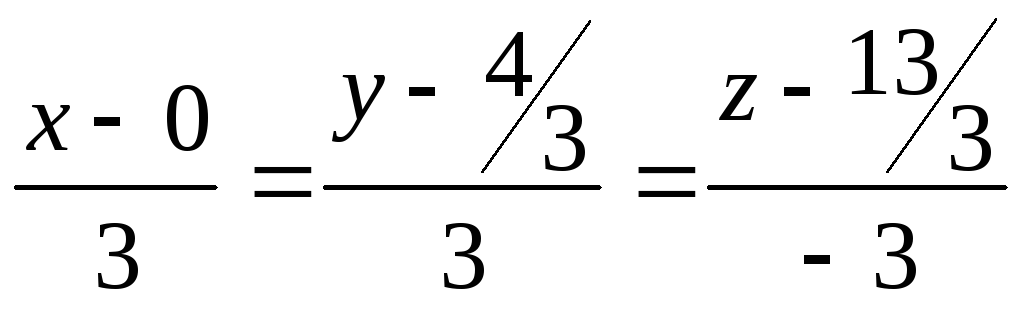
Угол между плоскостями α и β

№3 Угол между прямой и плоскостью

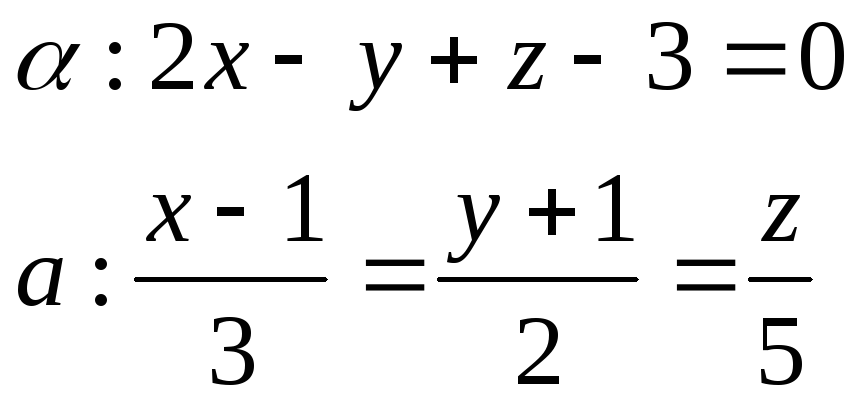
№4 Расстояние от прямой до плоскости

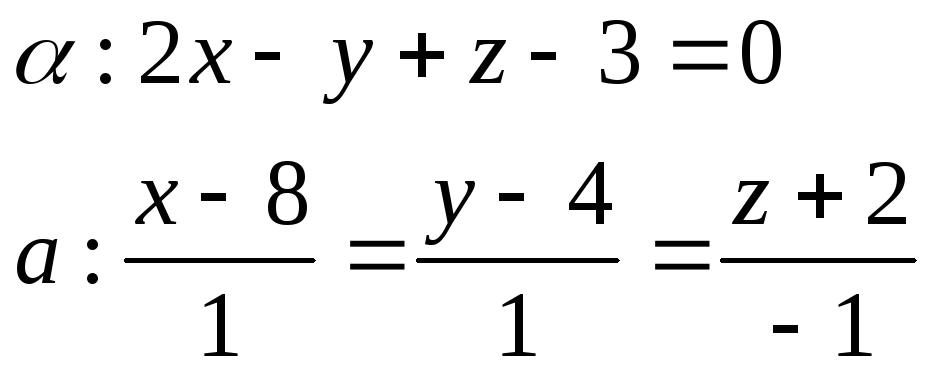
Расстояние от прямой до плоскости находится только тогда, когда они параллельны.