Определители

Матрица – это числа, объединенные в таблицу.

Матрицы бывают строкой, столбцом, прямоугольными и квадратными. Обозначаются большой буквой (А=), элемент – маленькой буквой с индексом (а_ij – i – строка, j - столбец).

В общем виде:

А=; В=(b₁₁ b₁₂ b₁₃)

Определитель – числовая характеристика квадратной матрицы (∆, D, det A). Вычисляется по правилу:

∆==a₁₁a₂₂-a₁₂a₂₁

∆==9+5=14

∆=

Метод треугольника: (+) (-)

Минор любого элемента определителя – это определитель меньше на один порядок, который получается, если вычеркнуть строку и столбец, в которых стоит данный элемент.

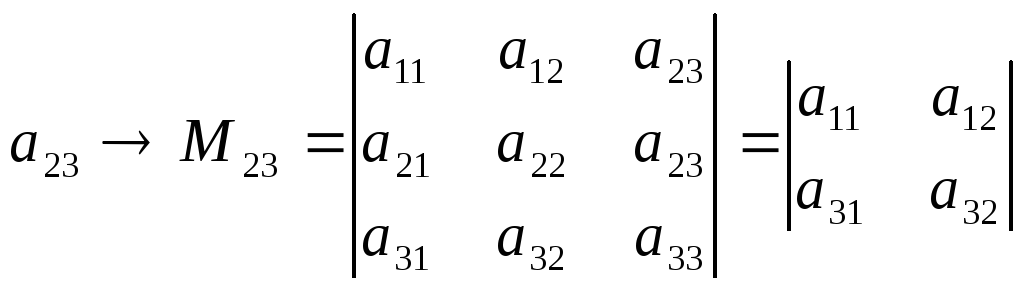
Алгебраическое дополнение элемента получается, если минор этого элемента умножить на знак (-1)^i+j.

Метод вычисления определителя с помощью алгебраических дополнений.

Теорема: Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Доказательство:

Аналогично можно доказать теорему для любой строки или столбца.

Свойства определителей:

1. Определитель не изменится, если его строки и столбцы поменять местами.

2. Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

3. Если элементы одной строки (столбца) пропорциональны соответствующим элементам другой строки (столбца), то определитель равен нулю.

4. Если все элементы любой строки (столбца) определителя умножить на число, то величина определителя умножится на это же число.

Используя это свойство можно вынести общий множитель элементов строки (столбца)

5. Определитель не изменяется, если вместо его строки записать сумму элементов этой строки с соответствующими элементами другой строки, умноженными на число.

Системы линейных уравнений

где а_ij – коэффициенты системы;

x_j - переменные;

b_i – свободные члены.

Система называется однородной, если все «b_i» равны нулю, система неоднородная, если хотя бы один «b_i» не равен нулю.

Система называется совместной, если имеет одно решение, несовместной – если имеет множество решений.

Решением системы называется набор чисел х₁…х_п, которые превращают все уравнения в верные тождества.

Решения систем методом Крамера:

;

Неоднородная система уравнений может быть записана

∆x₁=∆_x1

∆x₂=∆_x2

1. Если ∆, ∆х₁ и ∆х₂ ≠0, то решение единственно.

2. Если ∆=0, ∆х₁ или ∆х₂ ≠0, то решений нет.

3. Если ∆, ∆х₁, ∆х₂ =0, то решений множество.

Пример:

№1

№2

Решений система не имеет.

Однородная система линейных уравнений

1. Если ∆≠0, то система единственное нулевое решение.

2. Если ∆=0, то система имеет бесконечное множество решений.

Векторы и действия над ними

Вектор – направленный отрезок.

В координатном виде вектор записывается или .

Характеристики вектора:

1. Длина

2. Направление – задается направляющими косинусами

; ; ;

- единичный вектор, имеющий то же направление, что и , .

Замечание: Еденичные векторы, сонаправленные с осями координат называются ортами и обозначаются .

Равные вектора – вектора, у которых совпадают и длина и направление.

Нулевой вектор – длина равна нулю, направления нет (точка )

Коллинеарные вектора – вектора, лежащие на одной или параллельных прямых (сонаправлены или противоположно направлены), причем их длина не важна.

и - коллинеарные

k0 - векторы сонаправлены

k=1 – векторы равны

- векторы направлены противоположно

Признак коллинеарности:

Векторы компланарны – если три и более вектора лежат в одной плоскости.

Действия с векторами

1. Сложение – по правилам треугольника и параллелограмма

Свойства:

1.

2.

2. Вычитание – по правилам треугольника и параллелограмма

Характерные свойства такие же, как и для обычного вычитания.

3. Умножение на число

Свойства:

1.

2.

3.

4.

4. Скалярное произведение векторов

Работа есть скалярное произведение вектора силы на вектор перемещения.

Свойства:

1.

2.

3.

Применение скалярного произведения:

1.

2.

3.

Пример:

;; ;

;

Векторное произведение векторов

Векторное произведение на результатом имеет , обладающим следующими свойствами:

1. перпендикулярен плоскости, построенной на и .

2. Направлен так, чтобы поворот был против часовой стрелки.

3. Равен по величине площади параллелограмма, построенном на векторах и .

Пример:

Примечание:

1.

2. Момент силы

3.

Пример:

Смешанное произведение векторов

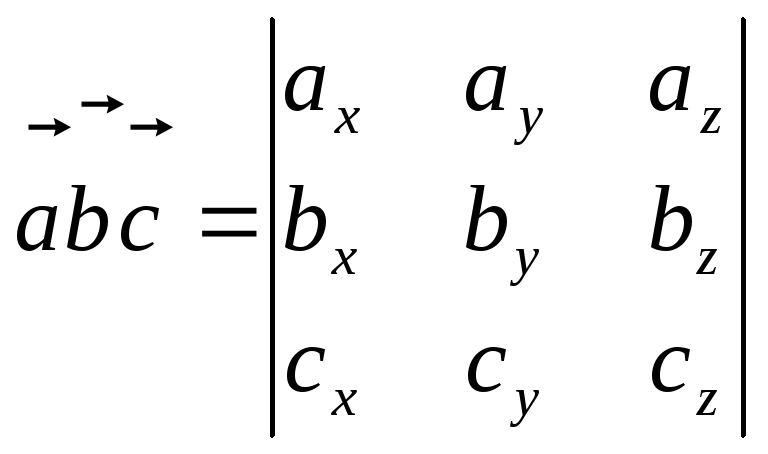
Свойства:

(перемещать только в круговом порядке!)

Примечание:

1. Объем параллелепипеда, построенного на трех векторах, равен модулю смешанного произведения трех векторов.

Признак компланарности:

2. Объем пирамиды

Пример:

№1 Проверить будут ли компланарны

Векторы - компланарны.

№2 Найти объем пирамиды, построенной на векторах

№3 Найти равнодействующую двух сил и работу, которую она совершает по перемещению точки А в точку В.

№4 Найти , приложенный к точке А относительно точки В.

Прямые на плоскости

Уравнением линии на плоскости ХОУ называется такое уравнение, содержащее переменные х, у, которое превращается в верное тождество для любой пары координат (х,у), если точка с этими координатами принадлежит линии и не выполняется, если точка не принадлежит линии.

Прямая на плоскости характеризуется нормальным вектором () и направляющим вектором ( парал а)

1. Общее уравнение прямой:

(1)

2. Уравнение прямой, проходящей через точку

(2)

3. Пусть 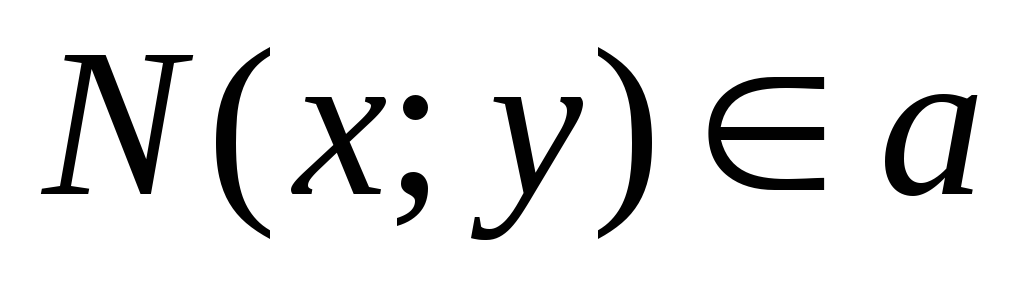, тогда - направляющий. Подставив в уравнение (2) координаты т. N мы получим скалярное произведение вектора на вектор

Так как это произведение равно нулю, то

Уравнение прямой с нормальным вектором , проходящей через т. М:

4. Подставим в уравнение (2) координаты т. N

(3) –

получим уравнение прямой, проходящей через две точки.

5. Так как М и N – заданные точки прямой, то - направляющий и можно обозначить ; (где ). Тогда уравнение прямой, проходящей через т. М с направляющим вектором имеет вид:

(4)

6. Система параметрических уравнений:

7. «Школьное уравнение»

(6)

Где (коэффициент наклона), .

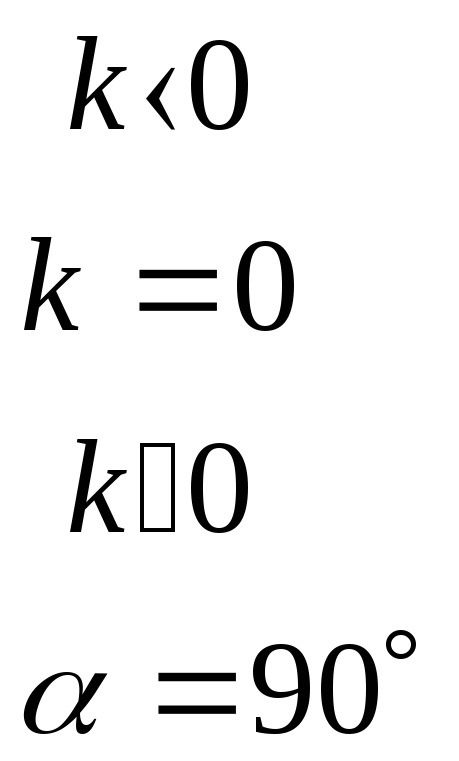
- длина отрезка, отсекаемого прямой от оси Оу. - проходит через начало координат.

8. Каноническое уравнение

(7)

где а, b – отрезки, отсекаемые от осей прямой.

9. Соотношения между прямыми:

а) a параллельна b (a║b)

1. коллениарен (║)

2. коллениарен

3. ()

б)

1. 2. 3. ║;

в) , φ – угол пересечения.

вычисляется с помощью arccos, если или если , то используется формула:

10. Расстояние от т. М () до прямой а с уравнением

Пример:

№1 Написать уравнение прямой, проходящей через т. К(-3;1) и т. Е(7;4)

Приведем уравнение к общему виду

Координаты вектора , вектора

№2 Дано уравнение прямой 2х+4у-1=0. Написать уравнение прямой, проходящих через т. А(1;1) а) b║а.