Основные формулы и понятия «Математического анализа»

При вычислении пределов часто используют следующие соотношения эквивалентностей:

- при x,

- при x;

- первый замечательный предел и следствия из него

,,

,;

- второй замечательный предел и следствия из него

,

,,

,,

где - бесконечно малая величина;

- бесконечно большая величина.

Функция y = f(x) с областью определения Dназывается непрерывной в точке, если выполняется условие

.

Если в точке x₀ нарушено хотя бы одно из условий, то x₀ называется точкой разрыва:

- предел слева; - предел справа.

Пример 1. Задана функция y = f(x). Найти точки разрыва функции, если они существуют.

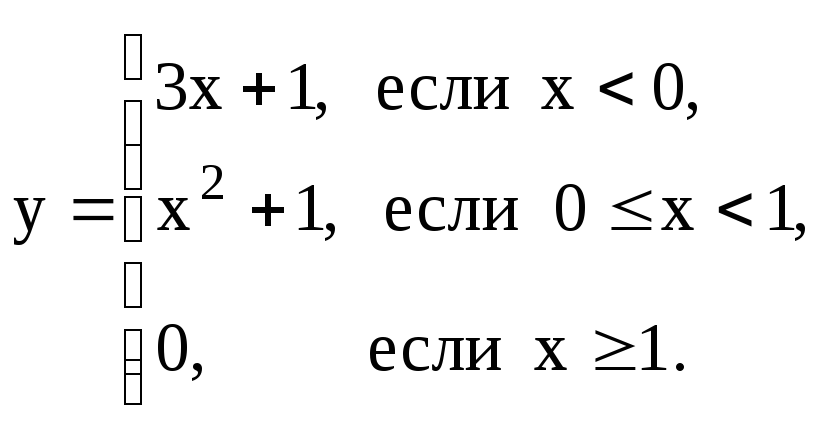
Решение. На каждом промежутке изменения независимой переменной функция непрерывна. Разрыв может быть только в точках «стыка». Проверим условие непрерывности в точках x = 0, x = 1 .

x = 0, ,,

.

В точке x = 0 выполняется условие непрерывности.

x = 1, ,,

.

Пределы слева и справа конечны, но не равны между собой. Следовательно, точка x = 1 является точкой разрыва первого рода.

Функции нескольких переменных

При изучении этой темы рекомендуется проводить аналогию с уже известными соответствующими фактами дифференциального исчисления функций одной переменной. Вместе с тем необходимо представлять, какие особенности возникают в трактовке того или иного понятия при переходе от функции одной переменной к многофакторной зависимости.

Приведем примеры некоторых функций, встречающихся в экономических задачах:

1 Функция Кобба–Дугласа - , гдеZ– величина общественного продукта, х – затраты труда,y– объем производственных фондов.

2 Издержки производства данного изделия при данной технике производства есть функция материальных затрат хи расходов на оплату рабочей силыy:

3 Пусть предметами потребления будут два товара А и В, цены которых исоответственно. Если цены других товаров постоянны, а доходы потребителей и структура потребностей не изменяются, то спрос и предложение каждого из товаров зависит от их цен:

а) — спрос на товар А;

б) — спрос на товар В;

в) — предложение товара А.

4 Функция затрат на приобретение товаров x иy .

Понятие частной производной также находит применение в экономике, например, расчет эластичности (см. далее).

Основные математические модели в экономике Непрерывное начисление процентов

Пусть начальный вклад в банк составил Q_Hденежных единиц. Банк выплачивает ежегодно Р % годовых. Необходимо найти размер вкладаQ_tчерез t лет. Размер вклада ежегодно увеличивается враз, то есть,,… .

Пусть процент начисляют nраз в году, тогда за-ю часть года процент начисления составит, а размер вклада за t лет при nt начислениях составит:

.

Примечание. При nпроцент начисляется непрерывно, при n = 2 - каждое полугодие, n = 4 - ежеквартально, n = 365 - каждый день.

Тогда при непрерывном начислении процентов

.

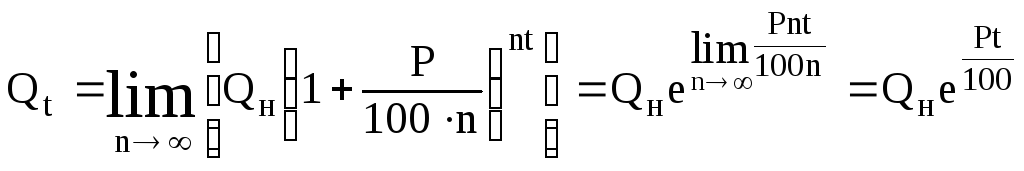Это есть экспоненциальный закон роста (при р>0) или убывания (при р<0). На практике в финансово-кредитных операциях непрерывное начисление процентов применяется очень редко. Оно эффективно при анализе серьёзных финансовых проблем, в частности, при обосновании и выборе инвестиционных решений.