
- •Высшая математика
- •1 Методические рекомендации по разделам
- •1.1 Аналитическая геометрия
- •1.2 Пределы. Дифференциальное исчисление функции одной переменной и его приложения
- •1.3 Матрицы. Функции нескольких переменных. Квадратичные формы
- •2 Задания для котнрольных работ и тестирования по разделам курса высшей математики
- •2.1 Аналитическая геометрия
- •2.2 Пределы. Дифференциальное исчисление и его приложения.
- •2.3 Матрицы. Функции многих переменных
- •3 Рекомендации составления тестов
- •3.1 Аналитическая геометрия
- •3.2 Пределы. Дифференциальное исчисление и его приложения
- •3.3 Матрицы. Функции многих переменных
- •Содержание
- •Обухов Анатолій Миколайович, Колесников Сергій Олексійович, Горшунов Борис Миколайович
- •84313, М. Краматорськ, вул. Шкадінова,72.
2.3 Матрицы. Функции многих переменных
Задание 13. Дана система линейных уравнений
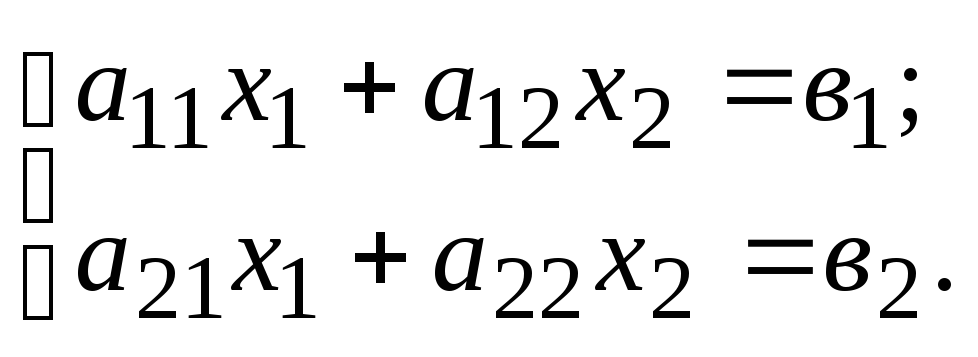
![]()
Необходимо:
а) записать матрицу системы, свободных членов и неизвестных;
б) записать систему в матричной форме;
в) вычислить определитель системы;
г) найти обратную матрицу системы;
д) записать решение системы в матричной форме;
е) найти собственные числа и собственные векторы матрицы системы.
Варианты заданий
1
![]() 1;
1;![]() 2;
2;![]() 4 ;
4 ;![]() 3;
3;![]() 5;
5;![]() 10 .
10 .
2
![]() 5;
5;![]() 4;
4;![]() 2 ;
2 ;![]() 3;
3;![]() 9;
9;![]() 7.
7.
3
![]() 5;
5;![]() 6;
6;![]() 8;
8;![]() 7;
7;![]() 22;
22;![]() 30.
30.
4
![]() -1;
-1;![]() -2 ;
-2 ;![]() -4
;
-4
;![]() -3;
-3;![]() 5;
5;![]() 10.
10.
5
![]() -2;
-2;![]() -3;
-3;![]() -5;
-5;![]() -4;
-4;![]() 5;
5;![]() 10.
10.
6
![]() 7;
7;![]() 8;
8;![]() 10;
10;![]() 9;
9;![]() -1;
-1;![]() 1.
1.
7
![]() -7;
-7;![]() -6;
-6;![]() -4;
-4;![]() -5;
-5;![]() -8;
-8;![]() -3.
-3.
8
![]()
![]() ;
;![]() -
-![]() ;
;![]() -
-![]() ;
;![]() -
-![]() ;
;![]() 2;
2;![]() 1 .
1 .
9
![]()
![]() ;
;![]()
![]() ;
;![]()
![]() ;
;![]()
![]() ;
;![]() 4;
4;![]() 12 .
12 .
10
![]() -3;
-3;![]() -4;
-4;![]() -7;
-7;![]() -5;
-5;![]() 1;
1;![]() -2
.
-2
.
11
![]() 4;
4;![]() 5;
5;![]() 7;
7;![]() 6;
6;![]() 13;
13;![]() 20.
20.
12.
![]()
![]() ;
;![]()
![]() ;
;![]()
![]() ;
;![]()
![]() ;
;![]() -6;
-6;![]() -10.
-10.
13
![]() -4;
-4;![]() -5;
-5;![]() -7;
-7;![]() -6;
-6;![]() -18;
-18;![]() -26
.
-26
.
14
![]() 8;
8;![]() 7;
7;![]() 5;
5;![]() 6;
6;![]() 15;
15;![]() 11.
11.
15
![]() 9;
9;![]() 8;
8;![]() 6;
6;![]() 7;
7;![]() 1;
1;![]() -1.
-1.
16
![]() 8;
8;![]() 9;
9;![]() 11;
11;![]() 10;
10;![]() -10;
-10;![]() -12.
-12.
17
![]() 10;
10;![]() 9;
9;![]() 7;
7;![]() 8;
8;![]() 39;
39;![]() 29.
29.
18
![]() 10;
10;![]() 11;
11;![]() 13;
13;![]() 12;
12;![]() -1;
-1;![]() 1.
1.
19
![]() -9;
-9;![]() -10;
-10;![]() -12;
-12;![]() -11;
-11;![]() -8;
-8;![]() 13.
13.
20
![]()
![]() ;
;![]()
![]() ;
;![]()
![]() ;
;![]()
![]() ;
;![]() 16;
16;![]() 8 .
8 .
21
![]()
![]() ;
;![]()
![]() ;
;![]()
![]() ;
;![]()
![]() ;
;![]() 5;
5;![]() 7.
7.
22
![]() 11;
11;![]() 12;
12;![]() 14;
14;![]() 13;
13;![]() 5;
5;![]() 20
20![]() .
.
23
![]() -11;
-11;![]() -10;
-10;![]() -8;
-8;![]() -9;
-9;![]() -32;
-32;![]() -25.
-25.
24
![]() 12;
12;![]() 11;
11;![]() 9;
9;![]() 10;
10;![]() 1;
1;![]() -1.
-1.
25
![]() -12;
-12;![]() -13;
-13;![]() -15;
-15;![]() -14;
-14;![]() 4;
4;![]() 13.
13.
Задание 14. Найти
производную функции
![]() в точкеМ
по направлению вектора
в точкеМ
по направлению вектора
![]() .
.
1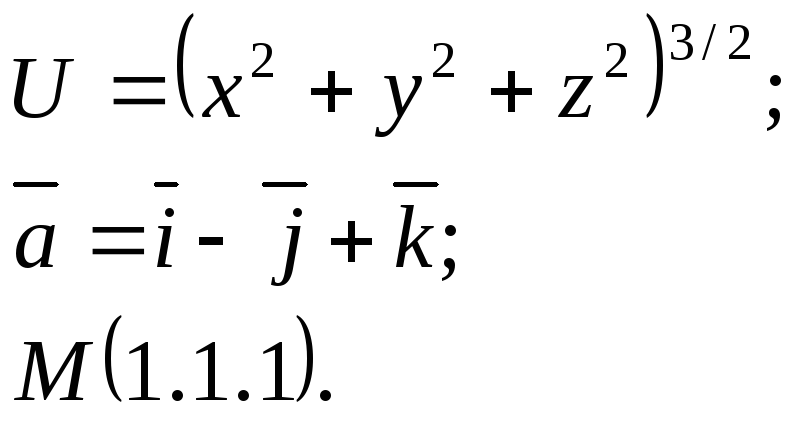 2
2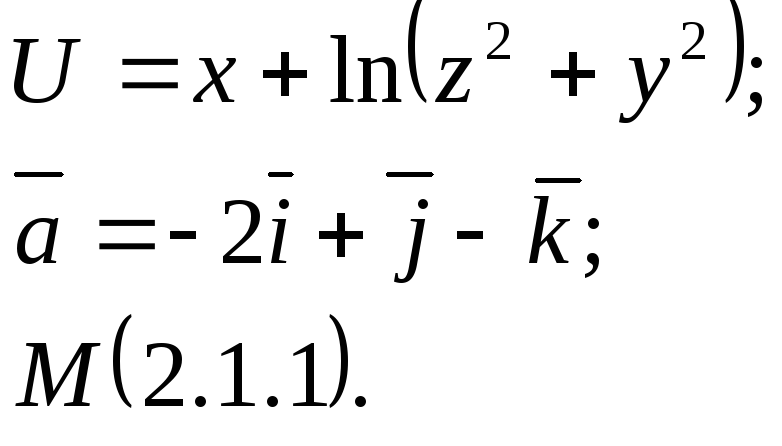
3
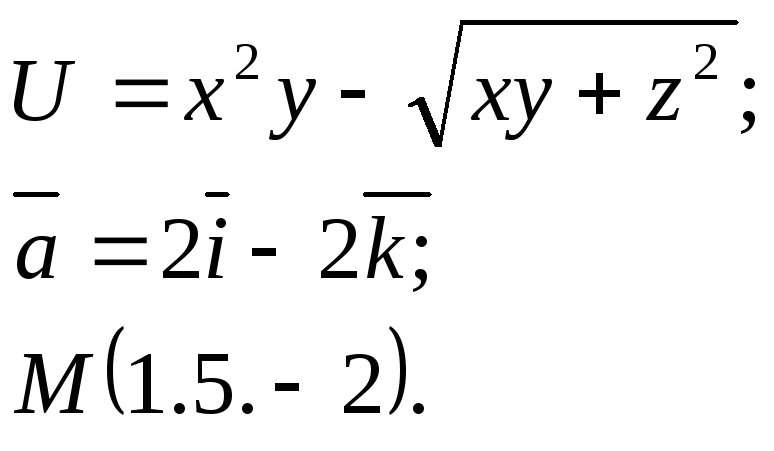 4
4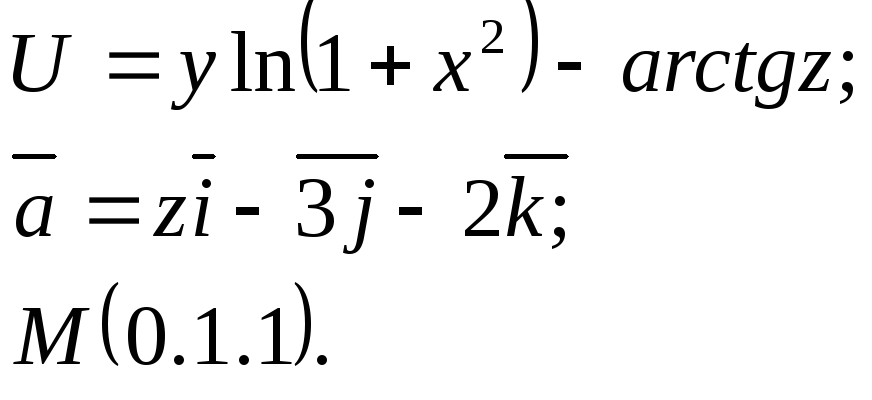
5
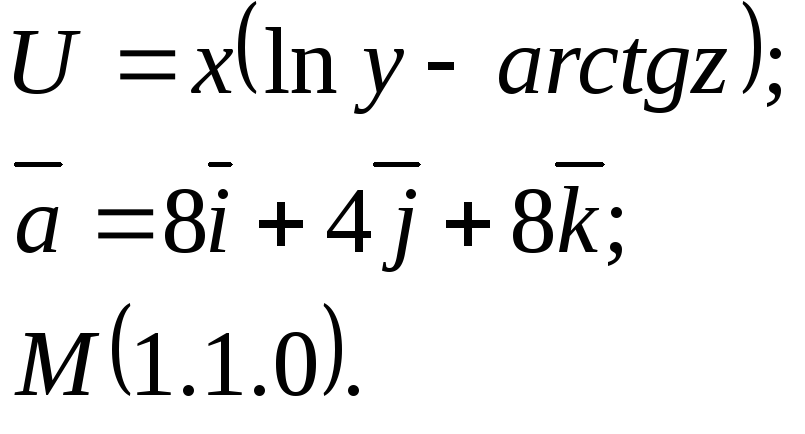 6
6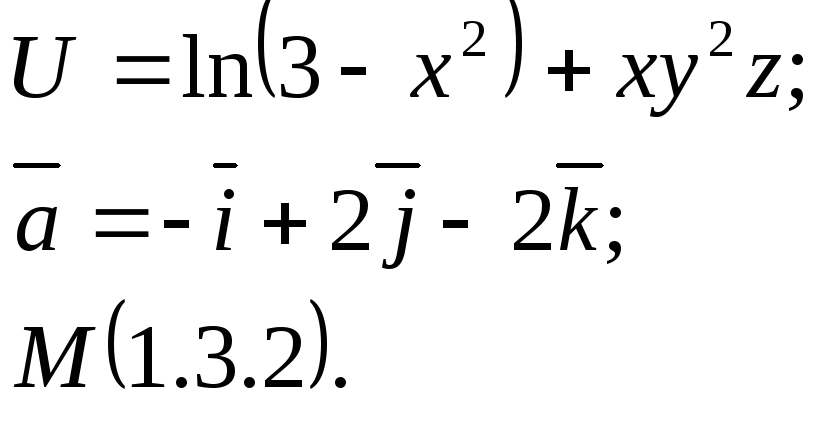
7
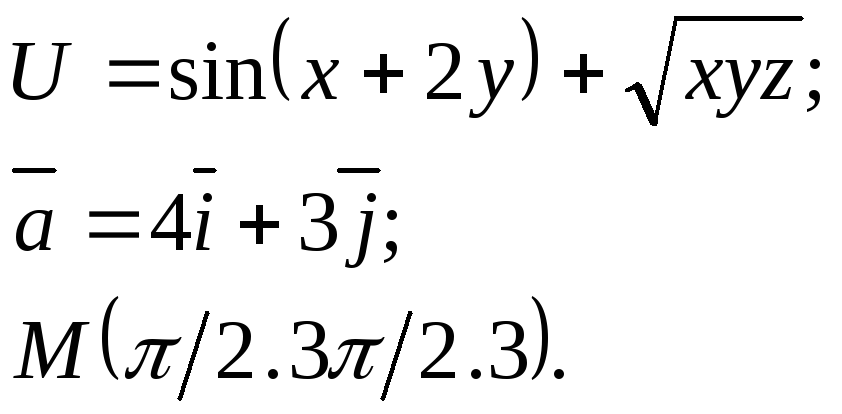 8
8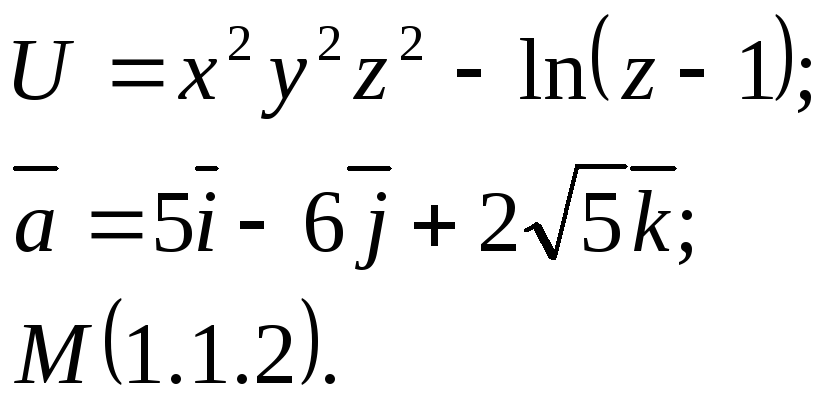
9
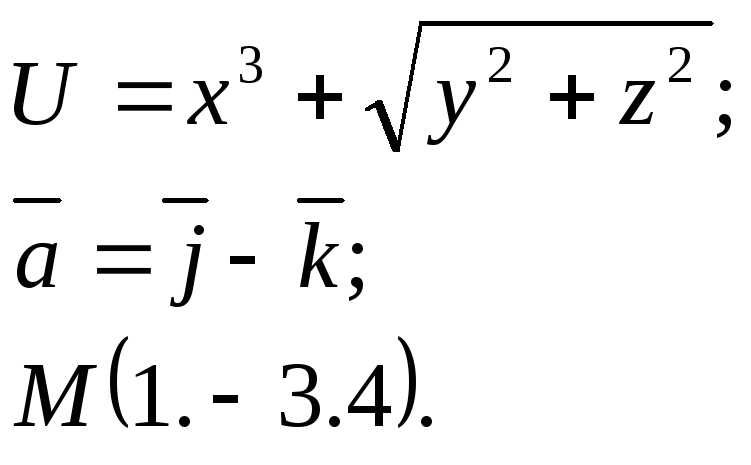 10
10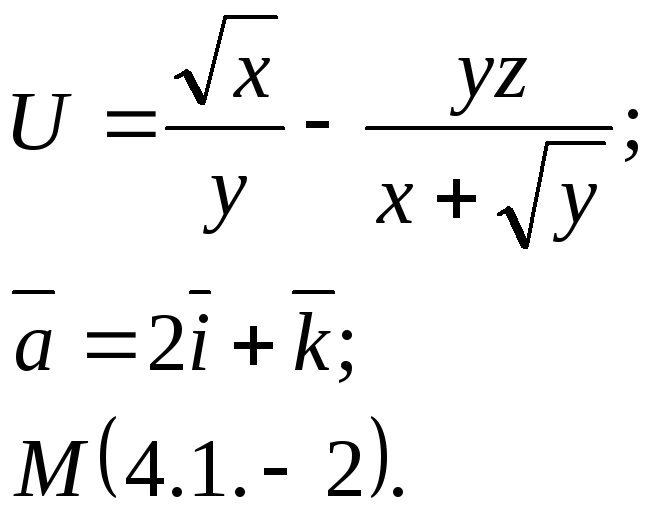
11
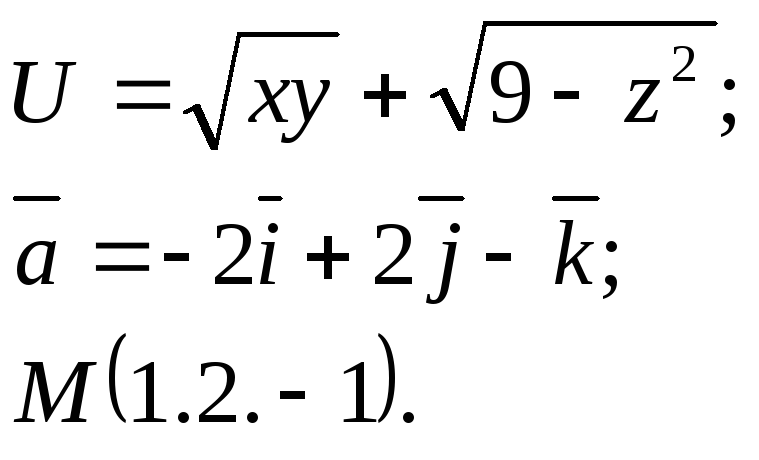 12
12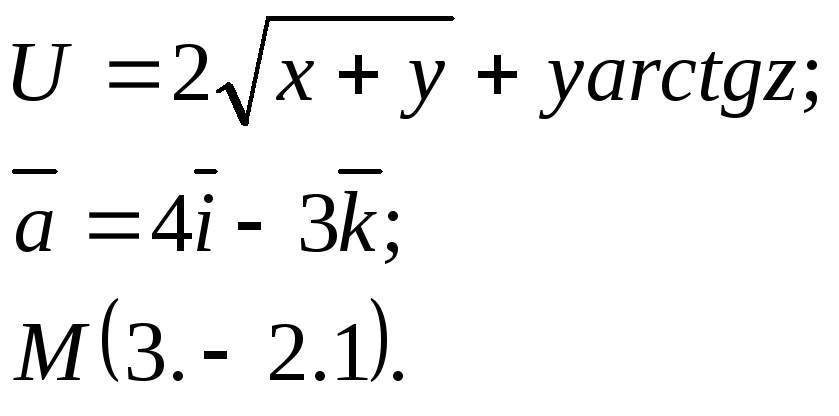
13
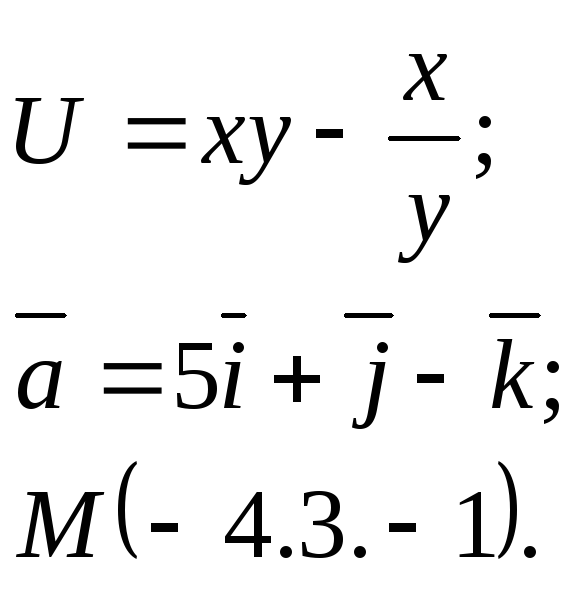
![]() 14
14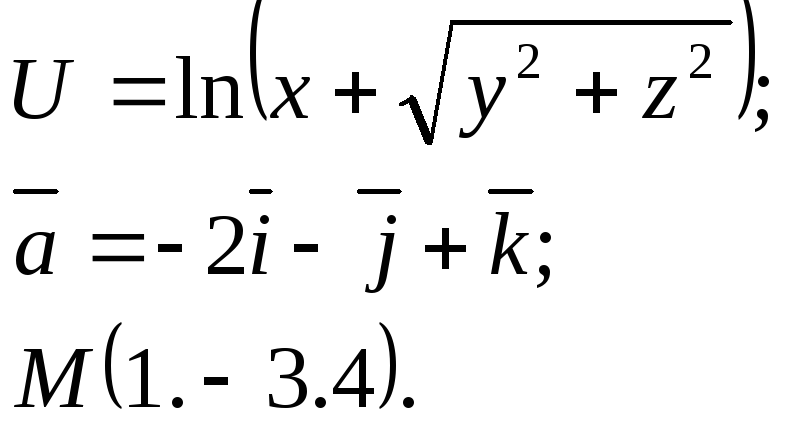
Задание
15. Найти угол между градиентами
функций![]() и
и![]() в точке М.
в точке М.
Варианты заданий
1
![]()
![]()
![]() .
.
2
![]()
![]()
![]()
3
![]()
![]()
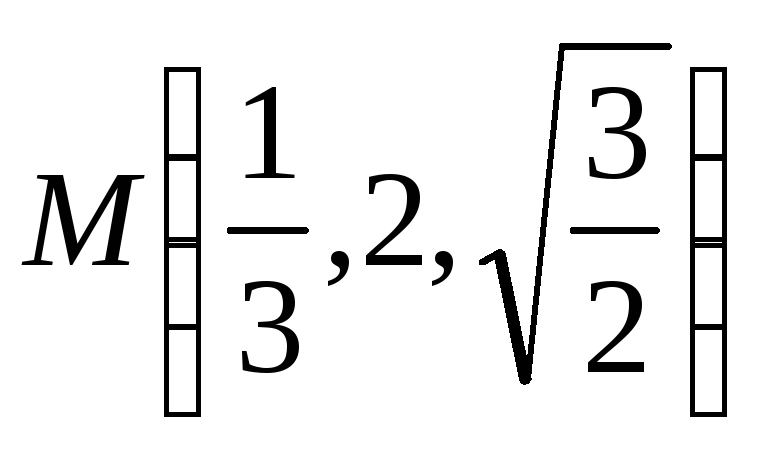 .
.
4
![]()
![]()
![]()
5
![]()
![]()
![]()
6
![]()
![]()
![]()
7
![]()
![]()
![]()
8
![]()
![]()
![]()
9
![]()
![]()
![]()
10
![]()
![]()
![]()
11
![]()
![]()
![]()
12
![]()
![]()
![]()
13
![]()
![]()
![]()
14
![]()
![]()
![]()
15
![]()
![]()
![]()
16
![]()
![]()
![]()
Задание
16. Найти наибольшее и наименьшее значение
функции
![]() в областиD.
ограниченной заданными линиями.
в областиD.
ограниченной заданными линиями.
Варианты заданий
1
![]()
![]()
2
![]()
![]()
3
![]()
![]()
4
![]()
![]()
5
![]()
![]()
6
![]()
![]()
7
![]()
![]()
8
![]()
![]()
9
![]()
![]()
10
![]()
![]()
11
![]()
![]()
12
![]()
![]()
13
![]()
![]()
14
![]()
![]()
15![]()
![]()
16
![]()
![]()
17
![]()
![]()
18
![]()
![]()
19![]()
![]()
20
![]()
![]()
21
![]()
![]()
22
![]()
![]()
23
![]()
![]()
24
![]()
![]()
25
![]()
![]()
26
![]()
![]()
Задание 17. Для функции двух переменных необходимо:
а) найти критические точки;
б) найти
![]() ;
;
в) вычислить
![]() ;
;
г) найти экстремальные значения функции.
Варианты заданий
1
![]() 2
2![]()
3
![]() 4
4![]()
5
![]() 6
6![]()
7
![]() 8
8![]()
9
![]() 10
10![]()
11
![]() 12
12![]()
13
![]() 14
14![]()
15
![]() .
.
16
![]() .
.
17![]() .
.
18
![]() .
.
19
![]() .
.
20
![]()
![]() .
.
21![]() .
.
22
![]() .
.
23
![]() .
.
24
![]() .
.
25
![]() .
.
26
![]() .
.
Задание
18. Для функции двух переменных
![]()
а) найти область определения функции;
б)
найти
![]() и
и![]() ;
;
в)
записать уравнение касательной плоскости
и нормали к поверхности ![]() в точке
в точке![]() .
.
Варианты заданий
1
![]() .
.
2
![]() .
.
3
![]() .
4
.
4![]() .
.
5
![]() .
.
6
![]() .
.
7
![]() .
.
8
![]() .
.
9
![]() .
10
.
10![]() .
.
11
![]() .
.
12
![]() .
.
13
![]() .
.
14
![]() .
.
15
![]() .
.
16
![]() .
.
17
![]() .
.
18
![]() .
.
19
![]() .
.
20
![]() .
.
21
![]() .
.
22
![]() .
.
23
![]() .
.
24
![]() .
.
25
![]() .
.
3 Рекомендации составления тестов
3.1 Аналитическая геометрия
Тест 1
1 Даны уравнения прямых: l1: 2x – y = 6; l2: 4x + 8y = –8. Построить их и найти точку пересечения.
2
Даны координаты вершин треугольника
А![]() (3,1),
А
(3,1),
А![]() (5,-2),
А
(5,-2),
А![]() (9,7).
Найти длину стороны
(9,7).
Найти длину стороны![]() .
.
3
Определить тип кривой и построить её:
![]() .
.
4
Даны координаты вершин треугольника:
![]() (6,
4, 2),
(6,
4, 2),![]() (10,
-1, -3),
(10,
-1, -3),![]() (12,
-2, -3). Найти вектор
(12,
-2, -3). Найти вектор![]() и уравнение прямой
и уравнение прямой![]() .
.
5
Даны координаты вершин пирамиды:![]() (6,
4, 2),
(6,
4, 2),![]() (10,
-1, -3),
(10,
-1, -3),![]() (12,
-2, -3),
(12,
-2, -3),![]() (-8,
8, -2). Найти ее объем.
(-8,
8, -2). Найти ее объем.
Тест 2
1 Даны уравнения прямых: l1: 2x – y = 6; l2: x + 2y = –2. Построить их и доказать аналитически перпендикулярность.
2
Даны координаты вершин треугольника
А![]() (3,1),
А
(3,1),
А![]() (5,-2),
А
(5,-2),
А![]() (9,7).
Найти уравнение прямой
(9,7).
Найти уравнение прямой![]() .
.
3
Определить тип кривой и построить её:
![]() .
.
4
Даны координаты вершин треугольника:
![]() (6,
4, 2),
(6,
4, 2),![]() (10,
-1, -3),
(10,
-1, -3),![]() (12,
-2, -3). Найти угол при вершине
(12,
-2, -3). Найти угол при вершине![]() .
.
5
Найти расстояние от точки
![]() до плоскости
до плоскости![]() .
.
Тест 3
1 Даны уравнения прямых: l1: 2x – y = 6; l2: 3x + 2y = 9. Построить прямую l1 и найти точки пересечения прямых l1 и l2 с координатными осями.
2
Даны координаты вершин треугольника:
А![]() (3,1),
А
(3,1),
А![]() (5,-2),
А
(5,-2),
А![]() (9,7).
Найти угол при вершине А
(9,7).
Найти угол при вершине А![]() .
.
3
Определить тип кривой и построить её:
![]() .
.
4
Даны координаты вершин треугольника:
![]() (6,
4, 2),
(6,
4, 2),![]() (10,
-1, -3),
(10,
-1, -3),![]() (12,
-2, -3). Написать уравнение плоскости
которой он принадлежит.
(12,
-2, -3). Написать уравнение плоскости
которой он принадлежит.
5
Написать уравнение прямой через точку
![]() перпендикулярно плоскости
перпендикулярно плоскости![]() .
.
Тест 4
1 Даны уравнения прямых: l1: 2x – y = 6; l2: -4x +2y = 9. Найти точку пересечения прямых и доказать их перпендикулярность.
2
Даны координаты вершин треугольника:
А![]() (3,1),
А
(3,1),
А![]() (5,-2),
А
(5,-2),
А![]() (9,7).
Найти уравнение медианы, проведенной
из вершины А
(9,7).
Найти уравнение медианы, проведенной
из вершины А![]() .
.
3
Определить тип кривой и построить её:
![]() .
.
4
Даны координаты вершин треугольника:
![]() (6,
4, 2),
(6,
4, 2),![]() (10,
-1, -3),
(10,
-1, -3),![]() (12,
-2, -3). Написать уравнение плоскости,
которой он принадлежит.
(12,
-2, -3). Написать уравнение плоскости,
которой он принадлежит.
5
Написать уравнение прямой через точку
![]() перпендикулярно плоскости
перпендикулярно плоскости![]() .
.
Тест 5
1
Даны точки: А![]() (3,1),
А
(3,1),
А![]() (5,-2).
Найти
(5,-2).
Найти![]() и
и![]() .
.
2
Даны координаты вершин треугольника:
А![]() (3,1),
А
(3,1),
А![]() (5,-2),
А
(5,-2),
А![]() (9,7).
Найти уравнение высоты проведенной из
вершины А
(9,7).
Найти уравнение высоты проведенной из
вершины А![]() .
.
3
Определить тип кривой и построить её:
![]() .
.
4.
Даны координаты вершин треугольника:
![]() (6,
4, 2),
(6,
4, 2),![]() (10,
-1, -3),
(10,
-1, -3),
![]() (12,
-2, -3). Написать уравнение плоскости
которой он принадлежит.
(12,
-2, -3). Написать уравнение плоскости
которой он принадлежит.
5
Написать уравнение прямой через точку
![]() перпендикулярно плоскости
перпендикулярно плоскости![]() .
.
