ММДО 3
.docГРАДИЕНТНЫЕ МЕТОДЫ РЕШЕНИЯ МНОГОМЕРНЫХ
ЗАДАЧ ОПТИМИЗАЦИИ
-
Цель работы
Закрепить теоретические сведения и приобрести практические навыки поиска безусловного экстремума функции многих переменных градиентным методом.
-
Условие задачи №1
Найдите минимум функции f(x1,x2) методом наискорейшего спуска, выбрав начальную точку X0. Исходные данные приведены в таблице. Дайте геометрическую иллюстрацию решения задачи.
|
Функция f(x1,x2) |
X0 |
|
2x1+0,4x |
(0,1) |
-2x2+0,4x
-5-
Расчетные формулы и алгоритм решения задачи
Для решения задачи поиска безусловного минимума функции широкое применение находят методы спуска. Суть их состоит в построении последовательности точек Xo,X1,...,Xk,..., таких, что f(Xo)>f(X1)>...>f(Xk)>...
В качестве начальной точки может быть выбрана любая точка, однако лучше, если точка Xo будет располагаться не слишком далеко от точки минимума. Затем необходимо выбрать направление, вдоль которого предполагается расположить следующую точку, и величину шага вдоль этого направления. В итеративных методах точки последовательности вычисляются по формуле
Xk+1= Xk + kPk, k=0,1,...,
где Pk - направление спуска; k- величина, определяющая длину шага.
Эти методы позволяют за конечное число шагов получить точку минимума или подойти достаточно близко к ней.
-
Решение задачи с графической иллюстрацией
f(x1,x2)
= 2x1+0,4x
-2x2+0,4x
-5.
1) Возьмем произвольную точку X0=(0,1). В этой точке f(X0)=-6,6. Вычислим координаты градиента функции в точке X0:
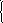1
f(X)
=
f(X)/
x1
=2 + 0,8x1;
2 f(X) = f(X)/ x2 = -2 + 0,8x2.
Тогда
2 f(X0) = -2+0,8*1 = -2,2;
f(X0) = (2;-2,2).
Поскольку f(X0) 0, то X0 не является точкой экстремума.
2) Переместимся из Х0 вдоль антиградиента - f(X0) в новую точку Х1 по формуле
X1 = X0 - 0 f(X0).
x21 = x20 -02 f(X0) = 1-1,20 ,
т.е. X1 = (0-20; 1-1,20).
Для определения координат точки Х1 нужно выбрать значение шага 0. Получим:
2 f(X1) = -2 + 0,8 ( 1-1,20 )= -1,2 –0,960;
f(X1) = (2–1,60; -1,2 –0,960).
Из соотношения ( f(Xk+1), f(Xk)) = 0 имеем:
(2–1,60)*2+(-1,2 –0,960)*(–1,2)=0.
Откуда 0 = 1,25.
3) При 0 = 1,25 уменьшение функции в направлении антиградиента достигает наибольшей величины. Осуществим спуск с выбранным шагом в точку X1:
x21 = 1–1,2*1,25 = 2,5;
X1 = (-2,5; 2,5).
Подставляя координаты точки Х1 в выражение, получим:
f(X1) = –10 < f(X0).
4) В точке Х1 имеем
1f(X1) = 2 + 0,8*(-2,5)= 0;
2f(X1) = –2+0,8*(2,5) = 0,
т.е. f ( –2,5; 2,5 ) = (0;0).
Значит, никакими перемещениями из точки Х1 функцию f(X) уменьшить нельзя и Х1 - искомая точка минимума Х*. Итак,
X*
= (x
,
x
)
= (–2,5; 2,5); fmin=
–10
Антиградиент –f(X0)=(2,5;–2,5) построен при начале координат. Траектория наискорейшего спуска Х0Х1 в точку минимума Х* параллельна антиградиенту -f(X0).
Известно, что квадратичную функцию можно представить следующим эквивалентным образом:
(x1
- x
)2
+ (x2
- x
)2
= (f - fmin)/a,
где
а
- коэффициент при x
и x
.
Это выражение задает уравнение семейства окружностей (линий уровня) радиуса
R
=
.
Для построения линий уровня поверхности f(X) ее уравнение приведем к виду (а=0,4):
(x1 + 2,5)2 + (x2 – 2,5)2 =( f + 10).
Линиями уровня поверхности (13) при f=c будут окружности. При f= 6; –6; –1; –9 их радиусы соответственно равны 4 ; 2; 3 ; 1 . На плоскости x1 О x2 они имеют общий центр (–2,5; 2,5).
-
Условие задачи №2
Найдите минимум функции f(x1,x2) методом наискорейшего спуска, выбрав начальную точку X0. Исходные данные приведены в таблице. Дайте геометрическую иллюстрацию решения задачи.
|
Функция f(x1,x2) |
X0 |
|
2x1+0,8x |
(0,1) |
-2x2+0,4x
-5-
Решение задачи с графической иллюстрацией
f(x1,x2)
= 2x1+0,8x
-2x2+0,4x
-5.
1) Возьмем произвольную точку X0=(0,1). В этой точке f(X0)=-6,6. Вычислим координаты градиента функции в точке X0:
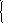1
f(X)
=
f(X)/
x1
=2 + 1,6x1;
2 f(X) = f(X)/ x2 = -2 + 0,8x2.
Тогда
2 f(X0) = -2+0,8*1 = -1,2;
f(X0) = (2;-1,2).
Поскольку f(X0) 0, то X0 не является точкой экстремума.
2) Переместимся из Х0 вдоль антиградиента - f(X0) в новую точку Х1 по формуле
X1 = X0 - 0 f(X0).
x21 = x20 -02 f(X0) = 1+1,20 ,
т.е. X1 = (0-20; 1+1,20).
Для определения координат точки Х1 нужно выбрать значение шага 0. Получим:
2 f(X1) = -2 + 0,8 ( 1+1,20 )= -1,2+0,960;
f(X1) = (2–3,20; -1,2+0,960).