Задание 7.

Задача класса «В». Исследовать функцию и построить график.

Общая схема исследования функции и построения графика:

1. найти область определения функции и точки разрыва;

2. определить, является ли функция четной или нечетной, периодической;

3. найти точки пересечения графика с осями координат и интервалы знакопостоянства функции;

4. найти асимптоты функции;

5. найти точки экстремума и интервалы монотонности функции;

6. найти точки перегиба и интервалы выпуклости и вогнутости графика;

7. построить график функции, используя результаты исследования и, при необходимости, построение по точкам.

Варианты для самостоятельного решения.

№1		№2		№3
№4		№5		№6
№7		№8		№9
№10		№11		№12
№13		№14		№15
№16		№17		№18
№19		№20		№21
№22		№23		№24
№25		№26		№27
№28		№29		№30

Задание 8.

Задача класса «А» . Найти наибольшее и наименьшее значения функции.

Общая схема исследования:

1. найти критические точки, лежащие внутри отрезка ;

2. вычислить значения функции на концах отрезка, то есть найти 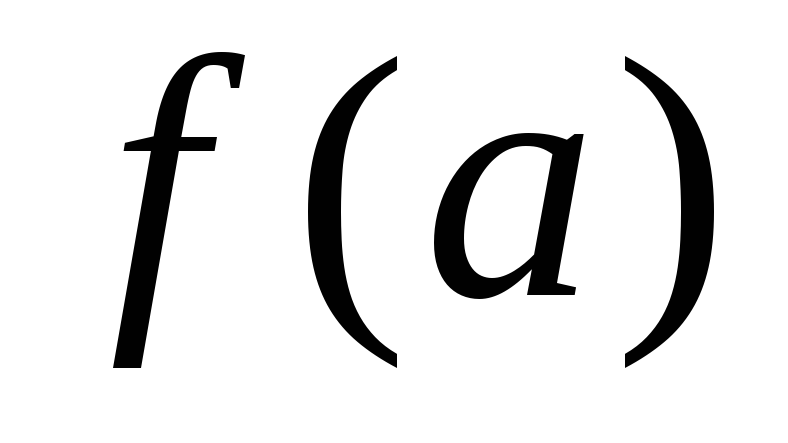и ;

3. сравнив найденные значения функции на концах отрезка со значениями функции в критических точках, выбрать наибольшее и наименьшее;

4. построить схематический график.

Варианты для самостоятельного решения.

№ 1		№ 2		№ 3
№ 4		№ 5		№ 6
№ 7		№ 8		№ 9
№ 10		№ 11		№ 12
№ 13		№ 14		№ 15
№ 16		№ 17		№ 18
№ 19		№ 20		№ 21
№ 22		№ 23		№ 24
№ 25		№ 26		№ 27
№ 28		№ 29		№ 30

Образец выполнения семестровой расчетно-графической работы Задание 1.

Решить данную систему по формулам Крамера, методом Гаусса и матричным способом

.

Решение.

1. Согласно формулам Крамера:

,

найдем

2. Проведем эквивалентные преобразования расширенной матрицы системы в соответствии с методом Гаусса:

3. Определим матрицу, обратную матрице . Такая матрица существует, так как определитель матрицыА не равен нулю (). Найдем алгебраические дополнения

Теперь транспонируем матрицу, составленную из алгебраических дополнений, и разделим ее элементы на , тогда обратная матрица

.

Вектор решений системы получим, умножив полученную обратную матрицу на вектор-столбец свободных членов:

.

Таким образом, всеми тремя способами получено решение: .

Задание 2.

Даны вершины треугольной пирамиды: (2;-3;1),(6;1;-1),(4;8;-9) и(2;-1;2).

Требуется найти:

1) длину ребра ;

2) площадь грани ;

3) угол между ребрами и;

4) объем пирамиды ;

5) уравнение плоскости АВС;

6) уравнения высоты, опущенной из вершины на грань;

7) уравнения стороны ;

8) длину высоты, опущенной из вершины на грань.

Решение.

1. Длина ребра определяется по формуле:

2. Площадь грани равна половине площади параллелограмма, построенного на векторахи. Так как

,, то

,то площадьтреугольника определяется по формуле

.

3) Косинус угламежду ребрамииопределяется по формуле. Найдеми, тогда

рад.

4) Объем пирамиды находим, используя формулу , определив предварительно

5) Найдем уравнение плоскости , используя уравнение плоскости, проходящей через три точки:

6) Канонические уравнения прямой, проходящей через данную точку параллельно вектору, имеют вид

.

В данном случае совпадает с нормалью, проведенной к плоскости грани, поэтому искомые уравнения имеют вид

7) Чтобы записать уравнения стороны , используем уравнения прямой, проходящей через две точки:

, тогда получим:

.

8. Найдем длину высоты, опущенной из вершины на грань, согласно формуле