
- •3 Уравнения динамики и динамические характеристики сау
- •3.1 Общий метод составления исходных уравнений
- •3.2 Передаточные функции систем автоматического регулирования
- •3.3 Законы регулирования
- •3.4 Структурные схемы и графы
- •3.5 Многомерные системы регулирования
- •3.6 Управляемость и наблюдаемость
- •3.7 Уравнения следящей системы
- •3.8 Линеаризация уравнений
- •3.9 О записи линеаризованных уравнений звеньев
3 Уравнения динамики и динамические характеристики сау
3.1 Общий метод составления исходных уравнений
Системы автоматического регулирования в большинстве случаев являются сложными устройствами, динамика которых описывается совокупностью дифференциальных уравнений. Для получения этой совокупности необходимо составить дифференциальное уравнение для каждого элемента автоматической системы так, чтобы общее число уравнений было не меньше, чем число независимых обобщенных координат, определяющих состояние системы.
При составлении дифференциального уравнения каждого элемента необходимо, прежде всего, выявить физический закон, определяющий его поведение. Таким законом может быть, например, закон сохранения вещества (объекты регулирования уровня, давления), закон сохранения энергии (объекты регулирования температуры), закон равновесия моментов (объекты регулирования скорости или угла поворота), закон равновесия электродвижущих сил (электрические цепи) и другие основные законы физики.
Математическое выражение, соответствующего физического закона и является исходным дифференциальным уравнением данного элемента автоматической системы.
Например, для электродвигателя закон равновесия моментов на его валу может быть записан в следующем виде:
![]()
где J и – приведенный момент инерции и угловая скорость двигателя; МВ – вращающий момент двигателя; МТ – тормозной момент внешних сил (момент нагрузки).
После записи дифференциального уравнения необходимо определить факторы, от которых зависят переменные, входящие в это уравнение.
Для приведенного выше примера необходимо установить, от каких величин зависят и какими выражениями определяются вращающий момент двигателя МВ и тормозной момент МТ на его валу. Нужно также выяснить. является ли приведенный момент инерции постоянной величиной или он изменяется в функции какой-либо переменной (например, в функции угла поворота двигателя).
Дальнейшим шагом является линеаризация полученных уравнений в соответствии с главой 3, если линеаризация вообще является допустимой. Обычно линеаризация допустима, если отсутствуют разрывные, неоднозначные или резко изгибающиеся характеристики и уравнения справедливы в течение всего интервала времени регулирования.
В
результате линеаризации получается
совокупность дифференциальных уравнений,
описывающих движение рассматриваемой
системы. Введя алгебраизированный
оператор дифференцирования
![]() ,
эту совокупность можно представить в
виде
,
эту совокупность можно представить в
виде
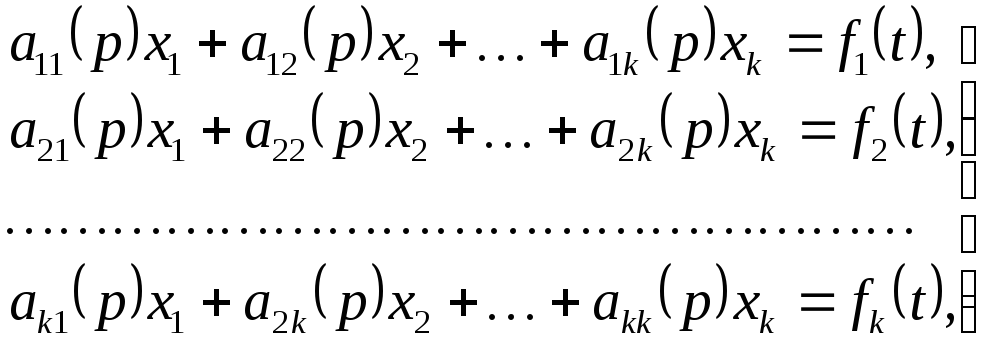 (3.1)
(3.1)
где
![]() обобщенные
координаты системы, в том числе и
регулируемая величина у
(t)
и
ошибка х
(t),
a
обобщенные
координаты системы, в том числе и
регулируемая величина у
(t)
и
ошибка х
(t),
a![]() функции
времени, представляющие собой задающие
и возмущающие воздействия. В дальнейшем
без потери общности рассуждений будем
считать, что к системе приложены только
два воздействия – задающее воздействие
g
(t)
и
возмущающее воздействии f(t).
Например,
можно положить, что
функции
времени, представляющие собой задающие
и возмущающие воздействия. В дальнейшем
без потери общности рассуждений будем
считать, что к системе приложены только
два воздействия – задающее воздействие
g
(t)
и
возмущающее воздействии f(t).
Например,
можно положить, что![]() ,
а
,
а
![]() .
Кроме того, в (3.1) введены некоторые
полиномы
.
Кроме того, в (3.1) введены некоторые
полиномы
![]() от
оператора р.
от
оператора р.
Совокупность
(3.1) может быть решена относительно любой
обобщенной координаты. Обычно она
решается либо относительно отклонения
регулируемой величины от заданного
значения, т. е. ошибки
![]() ,
либо
относительно регулируемой величины
,
либо
относительно регулируемой величины
![]() .
.
Первый случай встречается чаще, так как исследование изменения ошибки, как правило, является более важным. В этом случае получается дифференциальное уравнение
![]() (3.2)
(3.2)
Полином
D
(р) степени
п
от
оператора
![]() характеризует
свободное
движение
регулируемого объекта с регулятором.
Он называется характеристическим
полиномом и
может быть представлен в виде
характеризует
свободное
движение
регулируемого объекта с регулятором.
Он называется характеристическим
полиномом и
может быть представлен в виде
![]() (3.3)
(3.3)
где а0, . . ., ап в линеаризованной системе представляют собой постоянные коэффициенты.
Полином Q (р) той же степени
![]() (3.4)
(3.4)
где с0, . . ., сп – постоянные коэффициенты, определяют влияние задающего воздействия g (t) на характер изменения ошибки х (t). Под задающим воздействием g (t) здесь понимается требуемый закон изменения регулируемой величины у (t). Выражение Q (p) g (t) не равно нулю только в случае программного регулирования и в следящих системах. В системах автоматической стабилизации g (t) = const. Поэтому всегда можно выбрать начало отсчета так, чтобы g (t) = 0, что упрощает выражение (3.2).
Полином
N
(р) определяет
влияние возмущающего воздействия f(t)
на
характер изменения ошибки х
(t).
В
уравнении (3.2) учтено одно возмущение
f
(t),
действующее
на систему регулирования. В принципе
таких возмущений может быть несколько.
Однако вследствие линейности действует
принцип суперпозиции и достаточно
рассмотреть методику учета только
одного возмущения; при наличии нескольких
возмущений необходимо лишь просуммировать
результат. Если для какого-либо
возмущающего воздействия
![]() полином
NK
(р) =
0, то говорят, что система автоматического
регулирования является инвариантной
относительно этого воздействия.
полином
NK
(р) =
0, то говорят, что система автоматического
регулирования является инвариантной
относительно этого воздействия.
Равным образом в системах программного регулирования и в следящих системах равенство Q (р) = 0 означает, что система является инвариантной относительно задающего воздействия.
Из (3.2) вытекает, что ошибка системы автоматического регулирования может быть представлена в виде суммы двух составляющих. Первая составляющая определяется наличием задающего воздействия g (t). Вторая составляющая определяется наличием возмущающего воздействия (в общем случае – возмущающих воздействий или начальных условий). В системах автоматической стабилизации ошибка сводится только ко второй составляющей, т. е. определяется только наличием возмущающих воздействий.
При решении системы дифференциальных уравнений относительно регулируемой величины у (t) получается так называемое уравнение движения регулируемого объекта при наличии автоматического регулирования.
Это уравнение может быть получено в результате подстановки выражения для ошибки х (t) = g (t) — у (t) в уравнение (3.2):
![]() (3.5)
(3.5)
Степень
этого полинома т
![]() п:
п:
![]()
Как уже говорилось выше, в системах автоматической стабилизации при g (t) = const можно при соответствующем выборе начала отсчета получить g (t) = 0, что упрощает выражение (3.5).
При заданных функциях времени в правых частях дифференциальных уравнений (3.2) и (3.5) эти уравнения могут быть решены (проинтегрированы) относительно искомых функций времени, т. е. может быть найдено изменение ошибки регулирования во времени х (t) из (3.2) и движение регулируемого объекта вместе с регулятором у (t) из (3.5).
Уравнения (3.1) могут быть также представлены в форме Коши, т. е. в виде совокупности п уравнений первого порядка, где п – порядок полинома D (р):
![]() (3.6)
(3.6)
Здесь![]() ,
в
отличие от (3.1), представляют собой так
называемые фазовые координаты системы,
,
в
отличие от (3.1), представляют собой так
называемые фазовые координаты системы,
![]() – задающие и возмущающие воздействия,
а коэффициенты
– задающие и возмущающие воздействия,
а коэффициенты![]() и
и![]() суть
вещественные числа.
суть
вещественные числа.
Если
в (3.6) ввести алгебраизированный оператор
и обозначить
![]() ,
то
эта совокупность уравнений может быть
разрешена относительно любой из фазовых
координат
,
то
эта совокупность уравнений может быть
разрешена относительно любой из фазовых
координат
![]() .
.
