4.1.2 Уравнения систем с нелинейностью в виде сухого трения и зазора

Приведем примеры составления уравнений для нелинейных систем с сухим трением или зазором в механической передаче.

Следящая система с линейным и сухим трением. В§ 5.7составлены уравнения следящей системы в линейном виде. Рассмотрим теперь такой случай, когда к линейному моменту трениядобавляется еще момент сухого трения, имеющий постоянную величину, равную некоторому значениюс, и меняющий свое направление (знак) с изменением знака скорости вращения объектар(рис. 16.19). Следовательно, теперь уравнение управляемого объекта примет вид

,,, (4.48)

где – угол поворота вала управляемого объекта, причем

(4.49)

Важная особенность сухого трения состоит в том, что это (в отличие от релейных характеристик) далеко не всегда означает мгновенное переключение величины при. Здесь возможны два варианта:

(4.50)

В первом случае скорость объекта пройдет через нулевое значение, и его движение будет продолжаться без остановки дальше по закону (4.48). Во втором же случае произойдет остановка управляемого объекта, в течение которой будет иметь место не переключение, а медленное изменение величиныв интервале от(или обратно)будет принимать все время определенные значения

. (4.51)

В этом случае движение возобновиться снова только тогда, когда вращающий момент достигнет значения и превысит его.

Если же остается , то система будет неподвижна. Поэтому положение равновесия управляемого объекта оказывается неопределенным внутри некоторого отрезка, а именно, при любом значении. Этим определяется зона застоя системы. Застой проявляется в том, что, с одной стороны, система не будет двигаться при изменении угла задатчика в определенном интервале и, с другой стороны, что система будет обладать ошибкой из-за сухого трения в положении равновесия. В процессе же движения системы в одну сторону с любой скоростью сухое трение внесет постоянную ошибку одного знака, что соответствует как бы дополнительной внешней нагрузке.

Итак, уравнение управляемого объекта, как нелинейного звена системы, согласно (4.48) и (4.49) с учетом (4.50) будет иметь вид

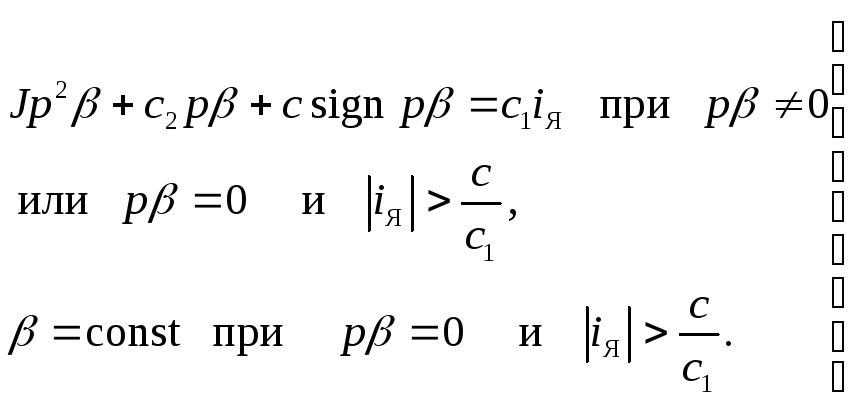(4.52)

Уравнения всех остальных звеньев данной следящей системы в совокупности образуют линейную часть системы, единое уравнение которой для свободного движения упрощенно запишем в виде

(4.53)

Следящая система с зазором. Предположим теперь, что в той же самой следящей системе нелинейность заключается не в сухом трении, а в наличии зазоров в силовой механической передаче между двигателем и управляемым объектом. Все эти зазоры объединим в один и изобразим его условно в виде вилки со свободным входом . Таким образом, между двигателем и управляемым объектом вклинивается теперь новое нелинейное звено, изображенное нарис. 16.20, а, входную величину которого обозначим через .

Характеристика этого нелинейного звена изображена на рис. 16.20, б. смысл ее следующий. Если бы не было зазора, то равнялось бы, и характеристикой была бы прямая под углом 45, изображенная на рис. 16.20, б штрих-пунктиром. Вследствие зазора при движении в сторону возрастания угла эта прямая сдвинется вправо на величину(поводок прижмется к правой стороне вилки). При изменении направления движения сначала поводок будет перемещаться внутри зазора, не двигая вилку (). На характеристике это соответствует горизонтальному отрезку длиной(AB или EF или KL или другие, в зависимости от фактического значения в это время). Затем начнет двигаться и вилка, что будет соответствовать прямойBC, сдвинутой влево от начала координат на величину .

При равновесии системы поводок и вилка могут занимать любое относительное положение внутри зазора, что вызывает ошибку системы из-за зазора, равную . При движении системы в одну из сторон будет постоянное отставание объекта из-за зазора на величину, не считая того отставания, которое будет еще из-за нагрузки.

Уравнение управляемого объекта, включающего в себя и двигатель, теперь разобьется на два нелинейных. Первое нелинейное уравнение управляемого объекта с двигателем будет (ограничимся учетом одной постоянной времени)

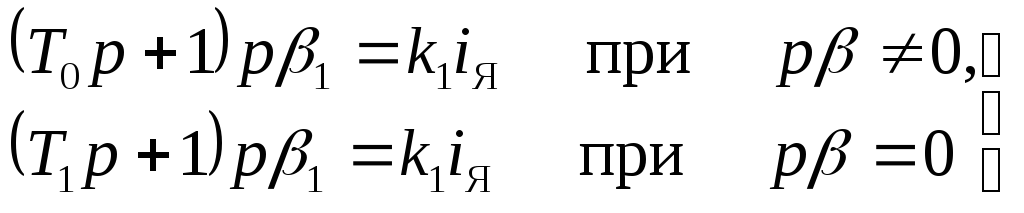(4.54)

(соответственно с поводком, прижатым к вилке, и с поводком, свободно двигающимся внутри зазора); меньшена величину, где– момент инерции управляемого объекта. Кроме этого, надо написать второе уравнение нелинейного звена с зазором, соответствующее характеристикерис. 16.20, б:

(4.55)

Следовательно, управляемый объект будет иметь остановки при своих колебаниях, соответствующие участкам АВ, CD и т. д. характеристики рис. 16.20, б.

Линейная часть системы остается такой же, как в предыдущем примере, т. е. (4.53).

Система автоматического регулирования давления (учет сухого трения). Рассмотрим систему (рис. 14.7), уравнения которой в линейном виде были получены в § 14.2. в чувствительном элементе 2 масса незначительна, но зато существенное значение может иметь сухое трение. Поэтому уравнение движения штока мембраны запишется в виде

, (4.56)

где – сила сухого трения, имеющая постоянную величинус, меняющая направление при изменении знака скорости ру (рис. 16.21, а) и могущая принимать любые значения во время остановки, т. е.

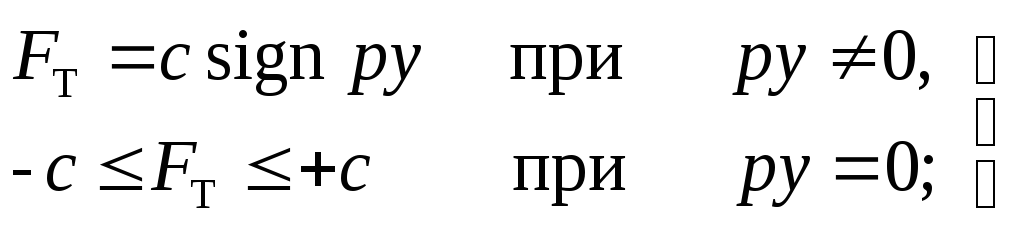(4.57)

Р – сила давления воздуха камеры на мембрану; – упругая сила мембраны;– сила пружины.

В результате после перехода к безразмерным относительным отклонениям (14.27) и (14.48), получим вместо (14.47) следующее уравнение чувствительного элемента как нелинейного звена:

(4.58)

где ;– площадь мембраны;– номинальное давление в камере.

Построим характеристику этого нелинейного звена с сухим трением в координатах . Легко видеть, что первое из уравнений (4.58) соответствует прямымDA и BC при и, а второе уравнение– отрезкамАВ, CD, EF, GH и т. п. на рис. 16.21, б. Из сравнения рис. 16.21, б и рис. 16.20, б видно, что сухое трение в таком нелинейном звене (без массы) эквивалентно зазору, половина которого равна , чего совершенно нельзя сказать о сухом трении в следящей системе, где учитывалась масса (момент инерции).

Все остальные звенья системы (рис. 14.7) образуют линейную часть, единое уравнение которой при будет

. (4.59)