5.7 Устойчивость двумерных систем с антисимметричными связями

В практике встречаются двумерные системы регулирования с антисимметричными связями. Структурная схема такой системы изображена на рис. 5.28. Она содержит два идентичных канала с одинаковыми передаточными функциями и антисимметричные связи. К такому виду сводятся некоторые гироскопические устройства, двухканальные системы слежения и др.

Рис. 5.28	Рис. 5.29

Матрица-столбец выходных (регулируемых) величин связана с матрицей столбцом ошибок выражением

(5.38)

Характеристическое уравнение замкнутой системы:

(5.39)

где I – единичная матрица 2×2.

Уравнение (5.39) можно представить в другом виде:

(5.40)

где корни уравнения (5.39)

(5.41)

Исследование (5.40) сводится к рассмотрению двух уравнений: и .Формально здесь может быть использован, например критерий Найквиста, но вместо точки комплексной плоскости (–1, j0), которая соответствует обычной записи характеристического уравнения , необходимо рассматривать две точки, соответствующие комплексным числам λ₁ и λ₂.

На рис. 5.29 изображена комплексная плоскость, на которой построены а. ф. х. частотной передаточной функции и комплексные числа, соответствующие λ₁ и λ₂. Замкнутая система будет устойчивой, если а. ф. х. устой­чивого или нейтрально-устойчивого в разомкнутом состоянии одного изоли­рованного канала не будет охватывать точек комплексной плоскости, соот­ветствующих λ₁ и λ₂.

Колебательная граница устойчивости будет иметь место, если выпол­няется одно из равенств: или .

Из (6.41) нетрудно видеть, что при а = 0 обе точки стягиваются в одну точку λ₁ = λ₂= -1, что соответствует обычной формулировке критерия Найквиста.

Другой метод расчета устойчивости заключается в том, что вводятся в рассмотрение комплексные величины

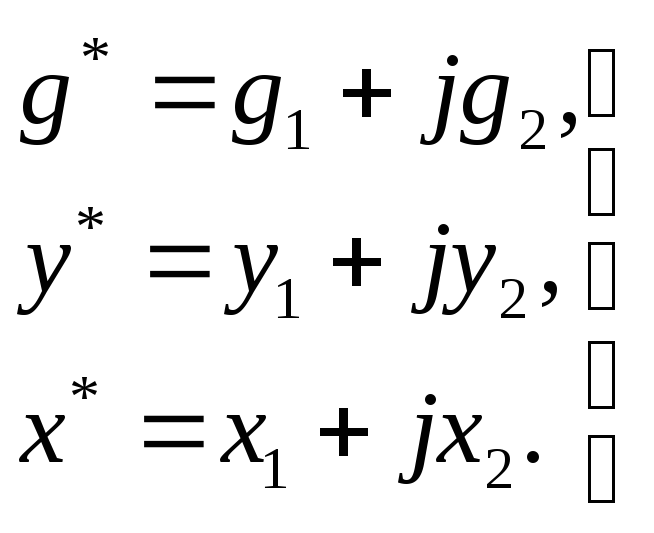(5.42)

Матричная зависимость (5.38) дает два равенства

(5.43)

Умножая второе равенство на j и складывая, получаем для комплексных величин

(5.44)

Здесь введена эквивалентная передаточная функция разомкнутой двумерной системы

(5.45)

Для дальнейшего расчета может использоваться критерий Найквиста в своей обычной формулировке. Однако при построении а. ф. х. частотной передаточной функции W_э (jω) она оказывается повернутой по сравнению с исходной а. ф. х. величины W₀ (jω) почасовой стрелке на угол α =arctg а. Это соответствует введению дополнительного фазового сдвига, что прибли­жает а. ф. х. к точке (–1, j0) и снижает запас устойчивости (рис. 5.30, а). Кроме, того, mod W_э (jω) оказывается в раз большеmod W₀ (jω), что также способствует снижению запаса устойчивости.

Рис. 5.30

При а < 0 поворот а. ф. х. будет против часовой стрелки и к точке (–1,j0) будет приближаться верхняя ветвь а. ф. х., соответствующая отрицательным частотам (рис. 5.30, б). Это также соответствует снижению запаса устойчивости.

Заметим, что и в случае перехода к комплексным величинам у* и х* по произвести расчет по а. ф. х. исходной одноканальной системы W₀ (jω). В этом случае колебательная граница устойчивости будет при выполнении условия

(5.46)

Условие (5.46) сводится к равенству

(5.47)

что согласуется с первым методом расчета устойчивости.

Рассмотренные методы позволяют упростить определение устойчивости двумерной системы по сравнению с использованием результирующего харак­теристического уравнения (5.39), так как требуют рассмотрения передаточной функции W₀ (р) одного изолированного канала