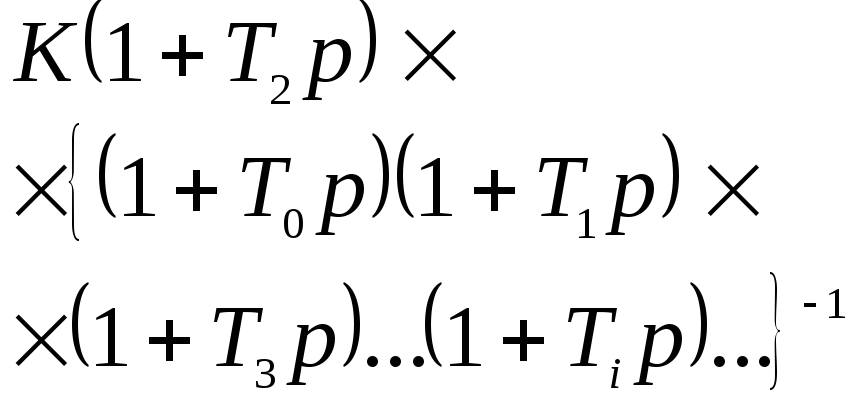Типовые передаточные функции

Тип ЛАХ	Степень астатизма	Дискретная частотная передаточная функция	Передаточная функция непрерывной части
I II III	0 1 2

Однако выше было показано, что ЛАХ дискретных систем, построенные в функции абсолютной псевдочастоты для частотпрактически сливаются с ЛАХ непрерывной части. Поэтому можно воспользоваться известными приемами расчета последовательных корректирующих средств, если в качестве желаемых ЛАХ использовать характеристики, соответствующие передаточным функциям непрерывной части.

Требуемый вид последовательного корректирующего звена определяется в этом случае по виду ЛАХ, полученным вычитанием ординат ЛАХ нескорректированной системы из ординат желаемой (типовой) ЛАХ.

Рассмотрим иллюстративный пример [10].

Пример. Произведем расчет системы с астатизмом первого порядка по следующим исходным данным: максимальная скорость слежения град/сек; максимальное ускорение слежения град/сек²; максимальная допустимая ошибка угл. мин.; допустимый показатель колебательностиМ = 1,5; шаг выдачи данных ЦВМ (период дискретности) Т = 0,02 сек; передаточная функция непрерывной части имеет вид

,

где сек, сек, сек.

Определим вид и параметры последовательного корректирующего звена, которое должно быть включено в непрерывную часть системы, а также необходимое значение общего коэффициента усиления .

Левее частоты среза ЛАХ дискретной системы совпадает с ЛАХ ее непрерывной части, а псевдочастота λ – с реальной частотой ω. Поэтому формирование желаемой ЛАХ левее частоты среза произведем обычными приемами.

Построим запретную зону для ЛАХ из условия точности (рис. 24.11). Контрольная частота

сек^-1.

Модуль передаточной функции разомкнутой системы при

дБ.

По этим данным на рис. 24.11 построены контрольная точка и запретная зона, сформированная из прямых с наклоном 20 и 40дБ/дек (наклоны 1 и 2).

Желаемая ЛАХ в низкочастотной области формируется так, чтобы она проходила выше точки на 3дБ (в линейном масштабе – ). Она состоит из отрезков прямых с наклонами 1–2–1. В низкочастотной области частотная передаточная функция разомкнутой системы имеет вид

.

Параметры желаемой ЛАХ и передаточная функция разомкнутой системы в низкочастотной области определим в следующем порядке.

Базовая частота ЛАХ

сек^-1.

Постоянная времени корректирующего звена, формирующая первый излом ЛАХ

сек.

Для получения заданного показателя колебательности должно выдерживаться условие (формула 12.86)

.

Отсюда получаем значение второй постоянной времени корректирующего звена:

сек.

Далее определяем необходимое значение общего коэффициента усиления:

сек^-1

и частоту среза ЛАХ

сек^-1.

Для обеспечения заданного показателя колебательности в высокочастотной области должно удовлетворяться неравенство (6.41):

,

где – сумма постоянных времени, меньших чем.

Отсюда получаем допустимое значение

сек.

На рис. 24.11 пунктиром построена ЛАХ непрерывной части нескорректированной системы, сплошной линией – желаемая (скорректированная ЛАХ) непрерывной части. В низкочастотной области (до частоты среза ) она совпадает с ЛАХ дискретной системы (см. рис. 24.10, а; на рис. 24.11 ЛАХ дискретной системы не изображена). В области высоких частот вид желаемой ЛАХ непрерывной части, вообще говоря, может быть произвольным. Важно только, чтобы сумма постоянных времени не превышала допустимого значения.

Наиболее простые корректирующие звенья получаются и в тех случаях, когда сопрягающие частоты ЛАХ нескорректированной системы и желаемой ЛАХ совпадают между собой. В рассматриваемом примере

.

Целесообразно принять

сек, сек.

Тогда

сек.

Вычитая из ординат желаемой ЛАХ ординаты характеристики нескорректированной системы, получим искомую ЛАХ последовательного корректирующего звена. Она соответствует интегро-дифференциальному звену с передаточной функцией

,

Где

сек, сек,

сек, сек.

Из приведенного примера видно, что при синтезе непрерывных, последовательных корректирующих устройств метод логарифмических частотных характеристик не теряет своей простоты и наглядности.

Можно показать [131], что при наличии временного запаздывания допустимый период повторения ЦВМ должен быть снижен в соответствии с формулой

, (6.48)

где – допустимый период повторения, полученный в результате синтеза системы без учета запаздывания. Время запаздывания, где1, 2, 3… и.

Если время запаздывания τ соответствует целому числу периодов, то формула (6.48) становится точной:

. (6.49)