793c6317f811408c88bf200ee564274a

Кодирование звуковой информации

С начала 90-х годов персональные компьютеры получили возможность работать со звуковой информацией. Звуковая волна - это непрерывная волна с меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон. Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).  Звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого участка устанавливается определенная величина амплитуды. Каждому участку присваивается определенный код. Этот процесс называется временной дискретизацией.  Естественно, чем меньше "размер" участка, тем выше качество звукозаписи. Представление непрерывного звукового сигнала в виде дискретных цифровых сигналов выполняют специальные устройства – аналогово-цифровые преобразователи (АЦП). Обратное преобразование для воспроизведения звука, закодированного числовым кодом, выполняют цифро-аналоговые преобразователи (ЦАП). АЦП и ЦАП являются компонентами звуковых карт. 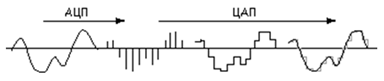Современные звуковые карты могут обеспечить 16, 32, 64- битную глубину кодирования, т.е. производят кодирование 2¹⁶,2³², 2⁶⁴ различных уровней сигнала. Количество различных уровней сигнала (состояний при данном кодировании) можно рассчитать по формуле: N = 2^I , где I - глубина звука. Качество кодирования зависит от количества измерений уровня сигнала в единицу времени, то есть частоты дискретизации. Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования. И так, качество двоичного кодирования звука определяется глубиной кодирования и частотой дискретизации. Количество измерений в секунду может лежать в диапазоне от 8000 до 48000, то есть частота дискретизации аналогового звукового сигнала может принимать значения от 8 до 48 кГц. При частоте 8 кГц качество дискретизированного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц – качеству звучания аудио-CD. Возможны как моно-, так и стереорежимы. при решении задач используются следующие понятия:  ^ Временная дискретизация – процесс, при котором, во время кодирования непрерывного звукового сигнала, звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина амплитуды. Чем больше амплитуда сигнала, тем громче звук. Глубина звука (глубина кодирования) - количество бит на кодировку звука.  Уровни громкости (уровни сигнала) - звук может иметь различные уровни громкости. Количество различных уровней громкости рассчитываем по формуле N= 2^I где I – глубина звука. ^ Частота дискретизации – количество измерений уровня входного сигнала в единицу времени (за 1 сек). Чем больше частота дискретизации, тем точнее процедура двоичного кодирования. Частота измеряется в герцах (Гц). 1 измерение за 1 секунду -1 ГЦ.  1000 измерений за 1 секунду 1 кГц. Обозначим частоту дискретизации буквой d. Качество двоичного кодирования – величина, которая определяется глубиной кодирования и частотой дискретизации. ^ Аудиоадаптер (звуковая плата) – устройство, преобразующее электрические колебания звуковой частоты в числовой двоичный код при вводе звука и обратно (из числового кода в электрические колебания) при воспроизведении звука. Характеристики аудиоадаптера: частота дискретизации и разрядность регистра.  Разрядность регистра -число бит в регистре аудиоадаптера. Чем больше разрядность, тем меньше погрешность каждого отдельного преобразования величины электрического тока в число и обратно. Если разрядность равна I, то при измерении входного сигнала может быть получено 2^I =N различных значений.  решение задач

Задача1.

Производится одноканальная (моно) звукозапись с частотой дискретизации 48 кГц и глубиной кодирования 16 бит. Запись длится 2 минуты, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 11 2)12 3) 13 4) 20 

Решение.

Так как звукозапись одноканальная (моно), значение величины оцифрованного канала умножается на 1. 

Частота дискретизации 48 кГц, следовательно, за одну секунду запоминается 48 000 значений сигнала. Так как глубина кодирования – 16 бит = 2 байта, для хранения 1 секунды записи требуется:

48 000 * 2 байта = 96 000 байт

Запись длиться 2 минуты = 120 секунд, следовательно, для хранения 2 минут записи требуется :

120 * 96 000 байт = 11 520 000 байт,

11 520 000 байт наиболее близко к объему файла 11 мегабайт.

Ответ: 11 мегабайт

2. Определить размер (в байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при частоте дискретизации 22,05 кГц и разрешении 8 бит. Файл сжатию не подвержен. ([1], стр. 156, пример 1) Решение: Формула для расчета размера (в байтах) цифрового аудио-файла: A=D*T*I/8. Для перевода в байты полученную величину надо разделить на 8 бит.  22,05 кГц =22,05 * 1000 Гц =22050 Гц A=D*T*I/8 = 22050 х 10 х 8 / 8 = 220500 байт. ^ Ответ: размер файла 220500 байт.

3.. Определить объем памяти для хранения цифрового аудиофайла, время звучания которого составляет две минуты при частоте дискретизации 44,1 кГц и разрешении 16 бит. ([1], стр. 157, №88)  Решение: A=D*T*I/8. – объем памяти для хранения цифрового аудиофайла.  44100 (Гц) х 120 (с) х 16 (бит) /8 (бит) = 10584000 байт= 10335,9375 Кбайт= 10,094 Мбайт.  Ответ: ≈ 10 Мб

4.. В распоряжении пользователя имеется память объемом 2,6 Мб. Необходимо записать цифровой аудиофайл с длительностью звучания 1 минута. Какой должна быть частота дискретизации и разрядность? ([1], стр. 157, №89)  Решение: Формула для расчета частоты дискретизации и разрядности: D* I =А/Т (объем памяти в байтах) : (время звучания в секундах):  2, 6 Мбайт= 2726297,6 байт D* I =А/Т= 2726297,6 байт: 60 = 45438,3 байт D=45438,3 байт : I Разрядность адаптера может быть 8 или 16 бит. (1 байт или 2 байта). Поэтому частота дискретизации может быть либо 45438,3 Гц = 45,4 кГц ≈ 44,1 кГц –стандартная характерная частота дискретизации, либо 22719,15 Гц = 22,7 кГц ≈ 22,05 кГц - стандартная характерная частота дискретизации Ответ:

	^ Частота дискретизации	Разрядность аудиоадаптера
1 вариант	22,05 КГц	16 бит
2 вариант	44,1 КГц	8 бит

5. Две минуты записи цифрового аудиофайла занимают на диске 5,1 Мб. Частота дискретизации — 22050 Гц. Какова разрядность аудиоадаптера? ([1], стр. 157, №94)  Решение: Формула для расчета разрядности: (объем памяти в байтах) : (время звучания в секундах): (частота дискретизации):  5, 1 Мбайт= 5347737,6 байт 5347737,6 байт: 120 сек : 22050 Гц= 2,02 байт =16 бит ^ Ответ: 16 бит

задачи для самостоятельного решения

1. Определить объем памяти для хранения цифрового аудиофайла, время звучания которого составляет две минуть частоте дискретизации 44,1 кГц и разрешении 16 бит.

2. Объем свободной памяти на диске — 5,25 Мб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 22,05 кГц?

3. Одна минута записи цифрового аудиофайла занимает на дис­ке 1,3 Мб, разрядность звуковой платы - 8. С какой частотой дискретизации записан звук?

4. Какой объем данных имеет моноаудиофайл, длительность звучания которого 1 секунда, при среднем качестве звука (16 бит, 24 кГц)?

5. Рассчитайте объем стереоаудиофайла длительностью 20 секунд при 20-битном кодировании и частоте дискредитации 44.1 кГц. 

6.Определите количество уровней звукового сигнала при использовании 8-битных звуковых карт. 

7.Оцените информационный объем стерео аудиофайла длительностью звучания 30 с, если "глубина" кодирования и частота дискретизации звукового сигнала равны соответственно 8 бит и 8 кГц;

8.Оцените информационный объем моноаудиофайла длительностью звучания 1 мин. если "глубина" кодирования и частота дискретизации звукового сигнала равны соответственно:16 бит и 48 кГц.

9.объем свободной памяти на диске — 0,01 Гб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 44100 Гц? ([1], стр. 157, №95) решение задач на кодирование текстовой информации

Что нужно знать:

• все символы кодируются одинаковым числом бит (алфавитный подход)

• чаще всего используют кодировки, в которых на символ отводится 8 бит (8-битные) или 16 бит (16-битные)

• при измерении количества информации принимается, что в одном байте 8 бит, а в одном килобайте (1 Кбайт) – 1024 байта, в мегабайте (1 Мбайт) – 1024 Кбайта 

• после знака препинания внутри (не в конце!) текста ставится пробел

• чтобы найти информационный объем текста I , нужно умножить количество символов N на число бит на символ K : I=N*K

Кодирование – отображение дискретного (прерывного, импульсного) сообщения в виде определенных сочетаний символов. Кодовая таблица (или кодовая страница) – таблица, устанавливающая соответствие между символами алфавита и двоичными числами.  ^ Примеры кодовых таблиц (к учебнику Н. Угринович):

• КОИ-7, КОИ-8 – кодирование русских букв и символов (семи-, восьми -битное кодирование)   1) #154 неразрывный пробел.

• ASCII –American Standard Code for Information Interchange (американский стандарт кодов для обмена информацией) – это восьмиразрядная кодовая таблица, в ней закодировано 256 символов (127- стандартные коды символов английского языка, спецсимволы, цифры, а коды от 128 до 255 – национальный стандарт, алфавит языка, символы псевдографики, научные символы, коды от 0 до 32 отведены не символам, а функциональным клавишам). 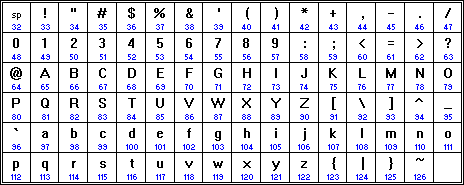1) #32 - пробел. Unicode – стандарт, согласно которому для представления каждого символа используется 2 байта. (можно кодировать математические символы, русские, английские, греческие, и даже китайские). C его помощью можно закодировать не 256, а 65536 различных символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов

• СР1251 - наиболее распространенной в настоящее время является кодировка Microsoft Windows, ("CP" означает "Code Page", "кодовая страница"). 1) #160 неразрывный пробел, 2)  #173 мягкий перенос.

• СР866 - кодировка под MS DOS  1) #255 неразрывный пробел. Мас – кодировка в ПК фирмы Apple, работающих под управлением операционной системы Mac OS.

1. #202 неразрывный пробел. ISO 8859-5 -Международная организация по стандартизации (International Standards Organization, ISO) утвердила в качестве стандарта для русского языка еще одну кодировку.  1) Коды 128-159 не используются; 2)  #160 неразрывный пробел,  3)  #173 мягкий перенос.  решение задач

Задача 1. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на 800 бит. Какова длина сообщения в символах? 1) 50 2) 100 3) 400 4) 800 Решение. Изменение кодировки с 16 бит на 8 бит, равно 16 - 8 = 8 бит .Следовательно информационный объем каждого символа сообщения уменьшился на 8 бит. Так как объем информационного сообщения уменьшился на 800 бит, следовательно количество символов в сообщение равно 800/8=100. Ответ: Длина сообщения - 100 символов.

Задача 2. В кодировке Unicode на каждый символ отводится два байта. Определите информационный объем слова из двадцати четырех символов в этой кодировке. 1) 384 бита 2) 192 бита 3) 256 бит 4) 48 бит Решение . Количество символов в сообщении - 24, каждый символ кодируется 2 байтами = 16 бит, следовательно 24 * 16 = 384 бит. Ответ: 384 бита

Задача3.. Сколько бит памяти займет слово «Микропроцессор»? Решение: Слово состоит из 14 букв. Каждая буква – символ компьютерного алфавита, занимает 1 байт памяти. Слово занимает 14 байт =14*8=112 бит памяти.  Ответ: 112 бит задача4. Текст занимает 0, 25 Кбайт памяти компьютера. Сколько символов содержит этот текст? ([1], c.133, №31) Решение: Переведем Кб в байты: 0, 25 Кб * 1024 =256 байт. Так как текст занимает объем 256 байт, а каждый символ – 1 байт, то в тексте 256 символов.  Ответ: 256 символов

задачи для самостоятельного решения

1.Автоматическое устройство осуществило перекодировку информационного сообщения длиной 48 символов, первоначально записанного в 7–битном коде ASCII, в 16–битную кодировку Unicode. При этом информационное сообщение увеличилось на 1) 48 байт 2) 96 байт 3) 54 байт 4) 432 байт

2.Автоматическое устройство осуществило перекодировку информационного сообщения, первоначально записанного в 7-битном коде ASCII, в 16-битную кодировку Unicode. При этом информационное сообщение увеличилось на 108 бит. Какова длина сообщения в символах? 1) 12 2) 27 3) 6 4) 62 3. Текст занимает полных 5 страниц. На каждой странице размещается 30 строк по 70 символов в строке. Какой объем оперативной памяти (в байтах) займет этот текст? ([1], c.133, №32) 4. Считая, что каждый символ кодируется одним байтом, оцените информационный объем следующего предложения из пушкинского четверостишия: Певец-Давид был ростом мал, Но повалил же Голиафа! (ЕГЭ_2005. демо, уровень А)

1)

400 бит

2)

50 бит

3)

400 байт

4)

5 байт

Кодирование графической информации

Методические рекомендации:

В задачах такого типа используются понятия:

• объем видеопамяти,

• графический режим,

• глубина цвета,

• разрешающая способность экрана,

• палитра.

Во всех подобных задачах требуется найти ту или иную величину.

Видеопамять - это специальная оперативная память, в которой формируется графическое изображение. Иными словами для получения на экране монитора картинки её надо где-то хранить. Для этого и существует видеопамять. Чаще всего ее величина от 512 Кб до 4 Мб для самых лучших ПК при реализации 16,7 млн. цветов.

Объем видеопамяти рассчитывается по формуле: V=I*X*Y, где I – глубина цвета отдельной точки, X, Y –размеры экрана по горизонтали и по вертикали (произведение х на у – разрешающая способность экрана).

Экран дисплея может работать в двух основных режимах: текстовом и графическом.

В графическом режиме экран разделяется на отдельные светящиеся точки, количество которых зависит от типа дисплея, например 640 по горизонтали и 480 по вертикали.  Светящиеся точки на экране обычно называют пикселями, их цвет и яркость может меняться. Именно в графическом режиме появляются на экране компьютера все сложные графические изображения, создаваемыми специальными программами, которые управляют параметрами каждого пикселя экрана. Графические режимы характеризуются такими показателями как:

- разрешающая способность (количество точек, с помощью которых на экране воспроизводится изображение)  - типичные в настоящее время уровни разрешения 800*600 точек или 1024*768 точек. Однако для мониторов с большой диагональю может использоваться разрешение 1152*864 точки.

- глубина цвета (количество бит, используемых для кодирования цвета точки), например, 8, 16, 24, 32 бита. Каждый цвет можно рассматривать как возможное состояние точки, Тогда количество цветов, отображаемых на экране монитора может быть вычислено по формуле K=2^I , где K – количество цветов, I – глубина цвета или битовая глубина.

Кроме перечисленных выше знаний учащийся должен иметь представление о палитре:

- палитра (количество цветов, которые используются для воспроизведения изображения), например 4 цвета, 16 цветов, 256 цветов, 256 оттенков серого цвета, 2¹⁶ цветов в режиме называемом High color или 2²⁴  , 2³² цветов в режиме True color.

Решение задач

Задача1. Черно-белое (без градаций серого) растровое графическое изображение имеет размер 10 ´10 точек. Какой объем памяти займет это изображение?( 2.68 [3])

Решение:

1. Количество точек -100

2. Так как всего 2 цвета черный и белый. то глубина цвета равна 1 ( 2¹ =2)

3. Объем видеопамяти равен 100*1=100 бит

. задача2.Для хранения растрового изображения размером 128 x 128 пикселей отвели 4 КБ памяти. Каково максимально возможное число цветов в палитре изображения. (ЕГЭ_2005, демо, уровень А). (См. также задачу 2.73 [3])

Решение:

1. Определим количество точек изображения. 128*128=16384 точек или пикселей.

2. Объем памяти на изображение 4 Кб выразим в битах, так как V=I*X*Y вычисляется в битах. 4 Кб=4*1024=4 096 байт = 4096*8 бит =32768 бит

3. Найдем глубину цвета I =V/(X*Y)=32768:16384=2

4. N=2^I , где N – число цветов в палитре. N=4

Задача3.. Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея- 800 х 600 пикселей? ([6], №63)

Решение:

1. Найдем объем видеопамяти для одной страницы: 800*600*24=11520000 бит =1440000 байт =1406,25 Кб ≈1, 37 Мб

2. 1,37*4 =5,48 Мб ≈5.5 Мб для хранения 4 страниц.

Задачи для самостоятельного решения

1.В процессе преобразования растрового графического изображения количество цветов уменьшилось с 65536 до 16. Во сколько раз уменьшится объем занимаемой им памяти?

2.В процессе преобразования растрового графического изображения количество цветов увеличилось с 16 до 42 949 67 296. Во сколько раз увеличился объем, занимаемый им в памяти?

3.Для хранения изображения размером 64x32 точек выделено 64 Кбайт памяти. Определите, какое максимальное число цветов допустимо использовать в этом случае.

4.Какой объем видеопамяти необходим для хранения двух страниц изображения при условии, что разрешающая способность дисплея равна 640 х 350 пикселей, а количество используемых цветов - 16?

5.Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея - 800 х 600 пикселей?

6.. Сколько секунд потребуется модему, передающему сообщения со скоростью 28800 бит/с, чтобы передать цветное растровое изображение размером 640 х 480 пикселей, при условии, что цвет каждого пикселя кодируется тремя байтами? (ЕГЭ_2005, уровень В)

Системы счисления

Решение задач

1.	Сколько единиц в двоичной записи десятичного числа 194,5?
	1)	5	2)	6	3)	3	4)	4

Решение:

1. Представим целую часть числа в двоичной системе счисления.

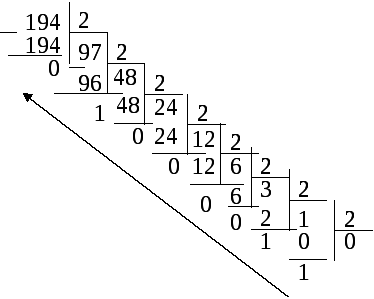
194₁₀ = 11000010₂

2. Представим дробную часть числа в двоичной системе счисления.

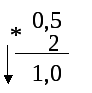
0,5₁₀=0,1₂

Таким образом, 194,5₁₀=11000010,1₂. В двоичной записи 4 единицы.

Ответ: 4

2. Дано А = 2478, B = A916. Какое из чисел C, записанных в двоичной системе, отвечает условию A < C < B ?
1) С = 101010002	2) С = 101010102	3) С = 101010112	4) С = 101011002
Решение: Для сравнения необходимо представить числа в одной системе счисления, в данном случае двоичной, т. к. варианты ответа – двоичные числа. Для этого каждую цифру восьмеричного числа заменим триадой (группой из 3 двоичных цифр): 247810 100 1112. Аналогично переведем шестнадцатеричное число, заменяя цифры четверкой двоичных цифр: A9161010 10012. Далее приступаем к сравнению: 101001112 < 101010002 и 101010002 < 101010012 (A < C < B). ( на этом можно остановиться, т.к. решение найдено.) 101001112 < 101010102 и 101010102 > 101010012 (A < B < C). 101001112 < 101010112 и 101010112 > 101010012 (A < B < C). 101001112 < 101011002 и 101011002 > 101010012 (A < B < C). Ответ: 1 Возможен способ решения, при котором сначала все числа переводятся в десятичную систему счисления, а затем сравниваются: 2478 =2 ∙ 82+4 ∙ 8+7=16710, A916=10 ∙ 16+9=16910. 101010002=1 ∙ 27+1 ∙ 25+1 ∙ 23=16810 (A < C < B). 101010102=1 ∙ 27+1 ∙ 25+1 ∙ 23+1 ∙ 2=17010 (A < B < C). 101010112=1 ∙ 27+1 ∙ 25+1 ∙ 23+1 ∙ 2+1=17110 (A < B < C). 101011002=1 ∙ 27+1 ∙ 25+1 ∙ 23+1 ∙ 22=17210 (A < B < C).

3. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 17 оканчивается на 2.

Решение.

Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления 17-2 = 15. Найдем делители числа 15, это числа 3, 5 ,15.

Выполним проверку, записав число 17 в системах счисления с основанием 3, 5 , 15:

17₁₀ = 122₃ = 32₅ = 12₁₅.

Ответ: 3, 5, 15.

Задачи для самостоятельного решения

1.Сколько значащих нулей содержится в двоичной записи суммы чисел а = 105₈ и b = С6₁₆?

1) 3 2) 4 3) 2 4) 5.

2. (Задание А1 демоверсии 2010 года (сайт fipi.ru))

Дано А=9D₁₆, B=237₈. Какое из чисел C, записанных в двоичной системе, отвечает условию A<C<B?

1) 10011010
2) 10011110
3) 10011111
4) 11011110

3.    Решение неравенств.

Поставьте вместо знака ? знак <, > или =.

• 285₁₀  ?  11D₁₆         

•  111111₂   ?   1111₈    

• 6С₁₆   ?   101001₂     

• 55₁₆   ?   125₈            

4. Расположите числа, записанные в различных системах счисления, в порядке возрастания:

35₁₀, 36₈, 3А₁₆, 100101₂      

5.. Перевести данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.

а) 666₍₁₀₎; б) 305₍₁₀₎; в) 153,25₍₁₀₎;

6.. Перевести данное число в десятичную систему счисления.

а) 1100111011₍₂₎; в) 10110101,1₍₂₎; д) 671,24₍₈₎; е) 41A,6₍₁₆₎.