olimpiady_matematika

ОТВЕТЫ И РЕШЕНИЯ. МОСКОВСКАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА

!

LXVIII Московская математическая олимпиада, 11 класс, 2005 г.

2.ОТВЕТ: 400.

3.РЕШЕНИЕ. Рассмотрим на доске произвольный клетчатый

квадрат со стороной 105, который назовем большим. Разобьем его на 25 квадратов 21 21, которые назовем малыми.

В каждом малом квадрате найдется хотя бы одна занумеро ванная клетка. Действительно, это либо центральная клетка это го квадрата, либо какая то другая клетка; иначе на расстоянии, меньшем 10 от центральной клетки, не найдется ни одной зану мерованной клетки, что противоречит условию задачи. Малые квадраты не пересекаются, поэтому в большом квадрате найдут ся по крайней мере 25 клеток с числами. Наименьшее из них от личается от наибольшего более, чем на 23. Соответствующие две клетки находятся на расстоянии, меньшем 150, поскольку лежат

вбольшом квадрате, расстояние между наиболее удаленными уг

ловыми клетками которого не превосходит 1052 < 150.

П р и м е ч а н и е. Размеры квадратов можно менять. Например, можно в качестве малых квадратов взять квадраты 19 × 19. Соответ ственно уменьшится и размер большого квадрата.

4. ОТВЕТ: 1) Да, вписанный четырехугольник при n = 3; 2) n0 = 6k, k N, например n0 = 6.

5. ОТВЕТ: 9, 11, 25.

РЕШЕНИЕ. Обозначим через a первое натуральное число, а через b и c записанные за ним двузначные числа. Пусть x — их сумма: x = a + b + c. Согласно условию числа a, b c и x удовлет воряют уравнению a•104 + 100b + c = x3. Покажем, что x < 100. Если x 100, то x3 104•x = 104(a + b + c) > 104•a + 100b + c, т. е.

64

уравнение не имеет решений. Следовательно, x — двузначное число, a — либо однозначное, либо двузначное число, а x3 либо пя ти , либо шестизначное число. Кроме того, x 22 (213 = 9261 — че тырехзначное число). Заметим, что x3 – x = 9999a + 99b, а зна чит, x3 – x делится на 99 нацело. Так как x3 – x = x(x – 1)(x + 1), то среди чисел x – 1, x, x + 1 какое то делится нацело на 9 и ка кое то на 11. Для x, удовлетворяющего условиям 22 x 99, воз можны следующие случаи:

1)x = 44 (x + 1 = 45), 443 = 85 184, 8 + 51 + 84 > 44;

2)x = 45 (x – 1 = 44), 453 = 91 125, a = 9, b = 11, c = 25;

3)x = 54 (x + 1 = 55), 543 = 157 464, 15 + 74 + 64 > 54;

4)x = 55 (x – 1 = 54), 553 = 166 375, 16 + 63 + 75 > 55;

5)x = 89 (x – 1 = 88, x + 1 = 90), 893 = 704 969,

70 + 49 + 69 > 89;

6)x = 98 (x + 1 = 99), 983 = 941 192, 94 + 11 + 92 > 98;

7)x = 99, x3 = 970 299, 97 + 2 + 99 > 99, 2 — не двузначное

число.

6. ОТВЕТ: Да.

LXIX Московская математическая олимпиада, 11 класс, 2006 г.

π

1. ОТВЕТ: -4- .

2. ОТВЕТ: a = 5, b = 2.

РЕШЕНИЕ. Пусть натуральные числа a и b взаимно просты, а десятичная запись числа a имеет n знаков. Тогда условие задачи записывается в виде уравнения

из которого следует, в частности, что a > b. В силу взаимной про стоты чисел a и b число a – b2 не имеет общих делителей ни с a, ни с b, следовательно, уравнение превращается в систему из двух уравнений

a– b2 = 1, 10n = ab.

Всилу все той же взаимной простоты чисел a и b (с учетом a > b), последнему уравнению удовлетворяют только пары чисел

a = 10n, b = 1 и a = 5n, b = 2n. Первая пара при подстановке дает

65

для числа n уравнение 10n = 2, которое не имеет решений. Если же a = 5n и b = 2n, получаем, что

а правая убывает, то это уравнение имеет не более одного корня, который угадывается: n = 1, откуда a = 5 и b = 2.

3.ОТВЕТ: нет.

4.ОТВЕТ: выигрывает Алиса.

5.ОТВЕТ: биссектриса угла без его вершины и фиксирован ной точки, а также отрезок, соединяющий основания перпенди куляров, опущенных из фиксированной точки на стороны угла (без концов).

РЕШЕНИЕ. Пусть A — вершина данного угла, O — фиксиро ванная точка на биссектрисе этого угла, OBC — рассматривае мый равнобедренный треугольник с вершиной в точке O (точки B и C лежат на сторонах угла), M — середина BC. Если точки B и C симметричны относительно прямой AO, то M лежит на луче AO, и наоборот, для любой точки M, лежащей на луче AO и от

66

Обратно, пусть M есть некоторая точка отрезка KL, не лежа щая на биссектрисе AO и отличная от точек K и L. Построим равнобедренный треугольник OBC такой, что точки B и C будут лежать на различных сторонах данного угла, а точка M будет слу жить серединой отрезка BC. Для этого проведем прямую, прохо дящую через точку M и перпендикулярную отрезку OM. Эта прямая пересечет стороны угла в точках B и C; покажем, что OB = OC. Так как углы BKO и BMO — прямые, то точки B, K, M, O лежат на одной окружности. Отсюда следует, что MBO = = MKO = BAO (последнее равенство вытекает из прямоуголь ного треугольника AKO, в котором KM AO). Обозначим каждый из этих углов через α. Поскольку OAC = OBC = α, то точки B, A, C, O лежат на одной окружности. При этом BAO = = OAC, значит, равны хорды BO и OC. Таким образом, тре угольник OBC — равнобедренный и BM = MC, т. е. M входит в искомое геометрическое место точек.

LXX Московская математическая олимпиада, 11 класс, 2007 г.

1.ОТВЕТ: может, 9.

2.ОТВЕТ: 4014.

3.ОТВЕТ: 6, 42, 1806.

4.ОТВЕТ: n = 5.

РЕШЕНИЕ. Применив в треугольниках SOA1, SOA2, ..., SOAn теорему синусов, получим, что

= SAnO, то sin SOA1 = sin SOA2 = ... = sin SOAn. Следова

67

S

Рис. 2

тельно, углы SOA1, SOA2, ..., SOAn могут принимать не более двух различных значений.

Если n 5, то среди углов SOA1, SOA2, ..., SOAn есть по крайней мере три одинаковых. Пусть, для определенности, это углы SOA1, SOA2, SOA3. Тогда равны треугольники SOA1, SOA2 и SOA3 (по двум сторонам и углу между ними, так как, очевидно, равны углы OSA1, OSA2 и OSA3). Значит, OA1 = OA2 = OA3 и O — центр окружности, описанной около треугольника A1A2A3 (рис. 2).

Пусть SH — высота пирамиды SA1A2A3. Тогда точка H также является центром описанной около треугольника A1A2A3 окруж ности (следует из равенства прямоугольных треугольников SHA1, SHA2 и SHA3), поэтому H = O.

При n = 4 из условия не следует, что SO — высота пирамиды. Например, если A1A2A3A4 — равнобокая трапеция, O — точка пе ресечения ее диагоналей, H — центр описанной около нее ок ружности, то для пирамиды SA1A2A3A4, в которой SH является высотой к основанию, выполнены все условия задачи (рис. 3).

Действительно, во первых, SA1 = SA2 = SA3 = SA4 в силу ра венства (по двум катетам) треугольников SHA1, SHA2, SHA3 и

SHA4, а во вторых, SA1O = SA2O = SA3O = SA4O в силу равенства (по трем сторонам) равнобедренных треугольников

68

2008). Так как 442 < 2008 < 452, то достаточно проверить дели мость 2008! на nn при n 45.

1)2008! делится на 4545 = 545•390, так как среди чисел 1, 2, ..., 2007, 2008 заведомо найдется 45 чисел, кратных 5, и 90 чисел, кратных 3.

2)2008! делится на 4646 = 246•2346, так как среди чисел 1, 2,

..., 2007, 2008 заведомо найдется 46 чисел, кратных 2, и 46 чисел, кратных 23 (23•46 = 1058 < 2008).

3)2008! не делится на 4747, так как число 47 простое, и поэто му среди чисел 1, 2, ..., 2007, 2008 есть лишь 42 числа, кратных 47 (47•42 = 1974 < 2008 < 2021 = 43•47).

Легко заметить, что для произвольного натурального x на

именьшим натуральным n, для которого x! не делится на nn, яв ляется наименьшее простое число p, большее x .

3.ОТВЕТ: невозможно.

4.Указание. Доказать, что OM — общая касательная к двум окружностям, описанным около треугольников ADO и OBC соответственно.

5.ОТВЕТ: 1) 2; 2) 2, 4, 38, 76.

6.ОТВЕТ: v 1 + 2 .

7.ОТВЕТ: 1) нет; 2) да; 3) да.

71

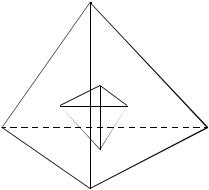
Тогда проекция тетраэдра ABCF на плоскость BCDE есть треугольник BOC, а проекция октаэдра ABCDEF на эту плос кость есть квадрат BCDE. Осталось заметить, что площадь тре

1

угольника BOC составляет ровно -4- от площади квадрата BCDE.

2) В произвольном многограннике Λ выберем четыре верши ны таким образом, чтобы они образовывали тетраэдр наиболь шего объема (если таких тетраэдров несколько, берем любой из них). Обозначим выбранные точки через A, B, C и D. Проведем через точку A плоскость α, параллельную плоскости BCD. Пусть E — какая нибудь вершина многогранника Λ. Тогда точка E ле жит по ту же сторону от плоскости α, что и точки B, C и D (или в плоскости α). Действительно, если бы это было не так, то объем тетраэдра EBCD был бы больше объема тетраэдра ABCD. Значит, и весь многогранник Λ лежит по одну сторону от плоскости α.

Аналогично рассмотрим плоскость β, проходящую через точку B и параллельную плоскости ACD, плоскость γ, проходя щую через точку C и параллельную плоскости ABD, и плоскость δ, проходящую через точку D и параллельную плоскости ABC. Пусть эти плоскости образуют тетраэдр A1B1C1D1 (A1 не лежит в плоскости α, B1 – в β, C1 — в γ, D1 — в δ). Многогранник Λ рас положен по одну сторону от каждой из плоскостей α, β, γ и δ, следовательно, он целиком содержится в тетраэдре A1B1C1D1 (рис. 6).

Из курса стереометрии известно, что в произвольном тетра эдре отрезки, соединяющие вершины с точками пересечения ме

D1

β

B1

Рис. 6

72