olimpiady_matematika

Если y = x , получаем квадратное уравнение относительно переменной y:

ay2 – y + 2 – 4a = 0,

где y > 0.

Для двух различных положительных решений уравнения не обходимо и достаточно выполнение следующих условий:

D > 0, yв > 0,

2 – 4a

----------------- > 0,

a

где D = (4a – 1)2, yв — абсцисса вершины параболы f(y) = ay2 – y + + 2 – 4a.

То есть:

4a – 1 = 0, a > 0,

При этом корни уравнения имеют вид:

Для получения единственного положительного решения уравнения рассмотрим 4 случая.

1)При a = 0 квадратное уравнение вырождается в линейное:

–y + 2 = 0, которое имеет единственный положительный корень y = 2.

2)При D = 0, yв > 0,

183

4) При f (0) = 0, yв > 0 уравнение имеет один положительный

1

корень, а второй корень, равный нулю, при этом a = -2- .

Объединяя все случаи, получим, что единственное положи тельное решение уравнения обеспечивается при

шение x = 4; y = 2.

x1 = 0, y1 = 2 – 4a; x2 = 4, y2 = 2. При a = 0 система имеет два решения:

x1 = 0, y1 = 2 и x2 = 4, y2 = 2.

AO = 5,

AO1 = 25 – 1 = 26 .

Отсюда следует, что

a = 62 .

184

T

E

K

B

A

O1 N

D

C

Рис. 76

2) Построим сечение пирамиды, заданной плоскостью

KMNE.

MN AD, BN : NC = 1 : 2,

TK = KA, TE : EC = 1 : 4.

3) Для вычисления площади сечения воспользуемся форму лой:

где Sпр — площадь ортогональной проекции на плоскость ABC,

ϕ— угол между плоскостью сечения и плоскостью ABC.

4)Определим площадь проекции (рис. 77) Sпр = SAMNE ′,

′— ортогональная проекция точки E на плоскость ABCточка

185

B

LM

N

D

A

E

Второй тур, 2009 г. Вариант 5

1. ОТВЕТ: 8.

РЕШЕНИЕ. Обозначим производительность первого рабочего через x деталей в единицу времени, производительность второго рабочего через y деталей в единицу времени, партию деталей че рез m. Очевидно, что m > 24. Пусть z — число деталей, которое осталось изготовить второму рабочему, когда первый выполнил всю работу.

Время, за которое первый рабочий сделал половину деталей,

m

равно --2--x- . Второму рабочему оставалось изготовить 24 детали,

186

m – 24

т. е. он сделал (m – 24) детали за время ------------------ . Составим уравне y

ние по условию задачи

m m – 24

----- = ------------------ .

2x y

Время, за которое второй рабочий выполнил половину рабо

время второй рабочий изготовил (m – z) деталей. По условию за дачи составим третье уравнение:

m m – z

---- = --------------- . x y

Система из первых двух уравнений приводится к квадратно му уравнению:

m2 – 52m + 480 = 0.

Корнями уравнения являются числа 40 и 12, из которых 40 удовлетворяет условию задачи. Из третьего уравнения находим z, равное 8.

187

Преобразуем исходное неравенство:

logx (49 – 84x + 36x2) < logx 1. Неравенство равносильно совокупности двух систем:

x > 1,

49 – 84x + 36x2 < 1;

0 < x < 1,

49 – 84x + 36x2 > 1.

шением второй системы — интервал x (0; 1).

7. ОТВЕТ: 7.

РЕШЕНИЕ. Обозначим сторону треугольника ABC за a. Рассмотрим BKL.

По теореме косинусов определим KL:

Аналогично в CLM определим

В KLM определим cos KLM по теореме косинусов:

Радиус описанного круга R = 7 . Из выражения:

KM

2R = ----------------------------

sin KLM

найдем сторону a, которая равна 7.

189

2π

8. ОТВЕТ: --3---- + 4 3 .

РЕШЕНИЕ. Рассмотрим уравнение y2 = 2(1 + cos 2x). Преобразуем выражение в правой части:

y2 = 4 cos2 x

или

|y| = 2 |cos x|

π

по условию |x| -2- , следовательно, |y| = 2 cos x.

Изобразим график, описываемый уравнением (рис. 78). Периметр прямоугольника ABCD равен P = 4PECOF.

PECOF = CF + OF, где OF = x, x 0; , CF = 2 cos x;

P = 4(x + 2 cos x).

Производная P ′ = 4(1 – 2 sin x) равна нулю при sin x = 1 .

2--

π

Максимум достигается при x = --6 .

190

получим:

4 > 0,

a < 0, a (– ; –1). a2 – 1 > 0;

Чтобы уравнение имело единственный отрицательный ко рень, необходимо и достаточно, чтобы параметр a определялся из следующей совокупности:

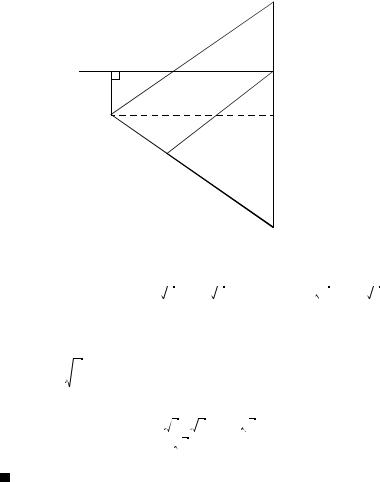
РЕШЕНИЕ. По условию задачи все боковые ребра пирамиды равны, следовательно, высота пирамиды TO, где точка O — се редина гипотенузы основания AC (рис. 79).

° l 2

В TBO TBO = 45 и TO = OB = ----2---- .

Площадь сечения пирамиды — это площадь TM′B, кото рая равна

1

S TM′B = -2- TB•hM′,

где hM′ — высота, опущенная из точки M′ на основание треуголь ника TB. Так как TB задано, то минимальная площадь сечения достигается при минимальном значении высоты hM′. Поэтому hM′ = ρ(AC, TB), где ρ(AC, TB) — расстояние между скрещиваю щимися прямыми AC и TB.

Для нахождения ρ(AC, TB) проведем через точку B прямую l, параллельную AC. Прямые TB и l определяют плоскость α. Так

192