140 Матеріали для факультативних занять, спецкурсів, гуртків. Математика 5–7
Приклад 5. Знайти остачу вiд дiлення многочлена
P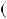 x
x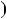
 2x3 3x2
2x3 3x2 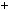 7x 1
7x 1
на двочлен x 1.
Розв’язання. Виконати дiлення «куточком».
|
2x3 |
|
|
|
|
3x2 |
|
7x |
|
1 |
x |
|
1 |
|
|
|
|
|
|
|
|
2x3 |
|
|
|
|
2x2 |
|
|
|
|
|
|
|
|
|
2x2 |
|
x 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
7x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6x |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
Вiдповiдь. 5.
У прикладi 5 остача вiд дiлення многочленiв є числом, тобто многочленом нульового степеня. Це не дивно, бо дiльник — многоч лен першого степеня.
Знайдемо значення многочлена P x при x |
1: |
|
|
|
|
|
|
|
|
|
|
|
P 1 |
2 13 |
|
|
3 12 |
7 1 |
|
|
|
1 |
|
|
2 |
|
3 |
7 |
|
1 |
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, P 1 |
5 i R |
5. Цей факт не є випадковим. |
|
|
|
|
|
|
|
|
Теорема 2 (теорема Безу*). Остача вiд дiлення будь якого мно |
гочлена P x на двочлен |
|
x |
|
a дорiвнює P a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доведення. Оскiльки дiльник x |
|
a — це многочлен першого сте |
|
пеня, то остача — число. Тодi P x |
|
x |
|
a Q x |
|
R. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При x a дiстанемо |
|
P a |
a |
|
a |
|
Q a |
|
R, |
звiдки R |
P a , |
що |
|
|
|
i треба було довести. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тепер ми можемо довести деякi твердження, якi були сформуль |
ованi в п. 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наслiдок 1. При будь якому натуральному n |
xn |
|
|
a n |
x |
|
|
a . |
|
|
|
Доведення. P x |
|
xn |
|
|
|
a n , S x |
|
x |
|
|
a. За теоремою Безу остача |
|
|
|
|
|
|
вiд дiлення P x |
на S x |
|
дорiвнює P a , тобто R |
P a |
|
a n |
|
a n |
0. |
|
|
Це означає, що P x дiлиться на S x , що i треба було довести. |
|
Наслiдок 2. При будь якому натуральному n |
x2n |
|
|
a2n |
|
x |
a . |
|
|
Доведення аналогiчне доведенню наслiдка 3.
*Безу Етьєн (1730–1783) — французький математик.
Розділ IV. Основи теорії подільності |
141 |
Наслiдок 3. При будь якому натуральному n 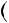 x2n
x2n 1
1 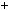 a2n
a2n 1
1 
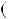 x
x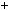 a
a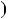 .
.
Доведення. P x
x
 x2n
x2n 1
1  a2n
a2n 1 ; S
1 ; S x
x
 x
x a
a  x
x 
 a
a . За теоремою Безу остача вiд дiлення P
. За теоремою Безу остача вiд дiлення P x
x на S
на S x
x дорiвнює P
дорiвнює P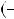 a
a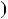 :
:
P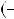 a
a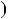

 a
a 2n
2n 1
1 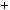 a2n
a2n 1
1 
 a2n
a2n 1
1 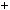 a2n
a2n 1
1  0.
0.
Отже, P x
x дiлиться на S
дiлиться на S x
x , що i треба було довести.
, що i треба було довести.
Для многочленiв, так само, як i для цiлих чисел, iснує поняття найбiльшого спiльного дiльника. Для знаходження НСД многоч ленiв також можна застосувати алгоритм Евклiда.
Приклад 6. Знайти найбiльший спiльний дiльник многочленiв
P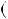 x
x
 x4
x4 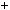 2x3 2x2 4x
2x3 2x2 4x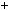 1 i S
1 i S x
x
 x2
x2 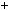 3x
3x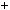 2.
2.
Розв’язання. Як було показано вище (див. приклад 4) при дiленнi P x
x на S
на S x
x остача R
остача R x
x
 x
x 3. За алгоритмом Евклiда НСД
3. За алгоритмом Евклiда НСД
P x ;S x  НСД S x ;R x .
НСД S x ;R x .
Подiлимо S x
x на R
на R x
x : x2
: x2  3x
3x 2 x
2 x 3
3
x2  3x x
3x x
2
Остача R1  2 — константа, це означає, що многочлени P
2 — константа, це означає, що многочлени P x
x i S
i S x
x взаємно простi.
взаємно простi.
Вiдповiдь. НСД  P
P x
x ;S
;S x
x
 2.
2.
Приклад 7. Знайти НСД  P
P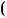 x
x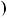 ;S
;S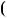 x
x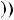 , якщо
, якщо
P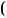 x
x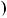
 6x4 2x3
6x4 2x3  5x2 x
5x2 x 1; S
1; S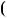 x
x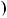
 6x3 2x2
6x3 2x2  3x 1.
3x 1.
Розв’язання. Подiлимо P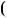 x
x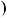 на S
на S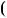 x
x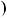 :
:
6x4 |
|
2x3 |
5x2 |
|
|
x 1 |
6x3 |
|
2x2 3x 1 |
|
|
|
|
6x4 |
|
|
2x3 |
3x2 |
|
|
x |
|
|
|
|
|
х |
|
|
|
|
|
2x2  1
1
R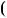 x
x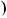
 2x2
2x2  1. Отже, НСД
1. Отже, НСД 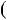 P
P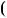 x
x ;S
;S x
x = НСД
= НСД  S
S x
x ;R
;R x
x .
.
Подiлимо S x на R x : |
6x3 |
|
|
2x2 |
3x |
|
|
1 |
|
2x2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6x3 |
|
|
|
0x2 |
|
|
|
|
|
|
|
|
|
|
|
3x |
3x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2x2 |
0x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x2 |
0x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|



 x
x




 .
. x
x
 x
x
 a
a
 x
x
 x
x a
a  x
x 
 a
a
 x
x
 x
x
 a
a



 1
1 

 1
1 
 1
1 
 дiлиться на
дiлиться на 
 , що i треба було довести.
, що i треба було довести. x
x
 x
x
 x
x
 x
x
 на
на 
 остача
остача 

 3. За алгоритмом Евклiда НСД
3. За алгоритмом Евклiда НСД
 на
на 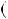
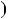 :
:  3
3 2
2  3
3
 2 — константа, це означає, що многочлени
2 — константа, це означає, що многочлени 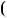
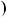 i
i 
 взаємно простi.
взаємно простi. P
P x
x
 x
x

 ;
;
 , якщо
, якщо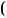 x
x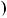



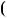 x
x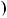


 на
на 
 :
: 1
1
 2
2 1. Отже, НСД
1. Отже, НСД 
 ;
;
 = НСД
= НСД 
 ;
;
 .
.
 P
P x
x
 x
x

 на
на 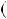
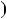 , якщо: а)
, якщо: а) 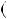
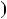

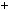 5
5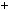 6,
6, 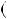
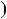

 2;
2;
 2
2
 2
2 2.
2. 1.
1. 6
6 11
11 6
6 3
3
 5
5 2
2
 19.
19. 1 простi. Чому дорiвнює
1 простi. Чому дорiвнює  2
2 7
7  5
5 12
12  6
6  19.
19. 1 i 6
1 i 6  1 — простi. Чому дорiвнює
1 — простi. Чому дорiвнює 