
b_667_Materialu-dlya-fakyltatuviv-5-7-klas
.pdf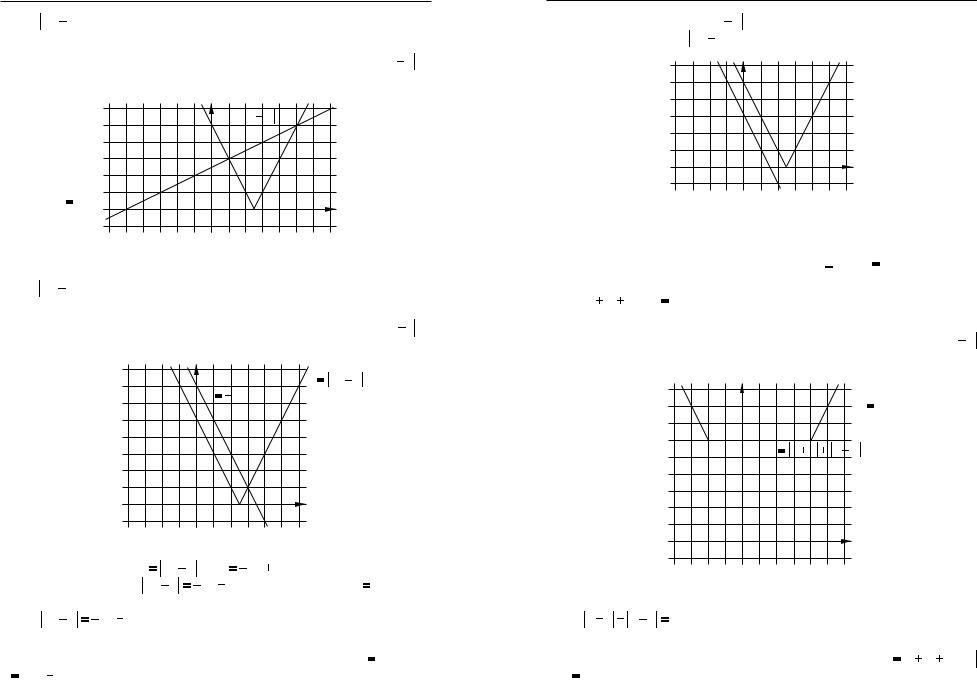
60 |
Матерiали для факультативних занять, спецкурсiв, гурткiв. Математика 5–7 |
Роздiл ІІ. Функцiї та графiки |
61 |
в) 2x 5 
 0,5x
0,5x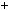 2,5.
2,5.
Розв’язання
Знайдемо абсциси точок перетину графiкiв функцiй y 
 2x 5 та y
2x 5 та y  0,5x
0,5x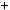 2,5 (рис. 34).
2,5 (рис. 34).
у
y 
 2x 5
2x 5
5
|
2,5 |
|
|
y 0,5x 2,5 |
1 |
|
|
|
|
|
|
–5 |
0 1 2,5 |
5 |
х |
Рис. 34
Вiдповiдь. 1; 5.
г) 2x 5 

 2x
2x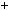 7.
7.
Розв’язання
Знайдемо абсциси точок перетину графiкiв функцiй y 
 2x 5 та y
2x 5 та y 
 2x
2x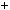 7 (рис. 35).
7 (рис. 35).
Графiки функцiй y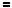
 2x 5 та y
2x 5 та y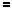
 2x
2x 3 не перетинаються. Це означає, що рiвняння 2x 5
3 не перетинаються. Це означає, що рiвняння 2x 5 
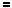
 2x
2x 3 коренiв не має.
3 коренiв не має.
5 |
|
у |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
||||||||
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
0 1,5 2,5 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 36 |
|
|
|
|
|
|
|
|
|
||||||
Вiдповiдь. Коренiв немає. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2. Розв’язування рiвнянь виду |
|
x |
|
a |
|
|
|
x |
|
b |
|
c |
||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
Приклади. Розв’язати рiвняння: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
а) |
|
x 2 |
|
|
|
x |
|
4 |
|
8. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання
Знайдемо абсциси точок перетину графiкiв функцiй y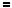
 x
x 2
2

 x 4 та y
x 4 та y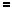 8 (рис. 37).
8 (рис. 37).
|
|
|
у |
|
|
|
y |
2x 5 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
у |
|
|
|
|
|
|
||
|
|
|
|
2x |
7 |
|
|
|
|
|
|
|
|
|
||
|
|
|
y |
|
|
|
|
8 |
|
|
|
|
y |
8 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
x |
2 |
x |
4 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
0 |
1 |
3 |
х |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 35 |
|
|
|
–3 –2 |
0 |
1 |
|
4 |
5 |
х |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
Графiки функцiй y |
2x |
5 та y |
|
2x |
7 перетинаються в однiй |
Рис. 37 |
|
|
|
|
|
|||||
точцi, отже рiвняння 2x |
5 |
2x |
7 має один корiнь: x |
3. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||
Вiдповiдь. 3. |
|
|
|
|
|
|
|
Вiдповiдь. –3; 5. |
|
|
|
|
|
|
|
|
д) 2x 5 |
2x 3. |
|
|
|
|
|
|
|
б) x 2 x 4 6. |
|
|
|
|
|
|
|
|
Розв’язання |
Розв’язання |
|||||||||||||||
|
Знайдемо абсциси точок перетину графiкiв функцiй y |
|
2x |
|
5 |
|
та |
Знайдемо абсциси точок перетину графiкiв функцiй y |
|
x 2 |
|
|
|
x |
|
4 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
y |
|
2x 3 (рис. 36). |
та y 6 (рис. 38). |
||||||||||||||
|
|||||||||||||||||
62 |
Матеріали для факультативних занять, спецкурсів, гуртків. Математика 5–7 |
|||||||||||||
|
Ми бачимо, що при |
|
2 |
|
x |
|
4 графiки цих функцiй спiвпадають. |
|||||||
|
|
|||||||||||||
Це означає, що рiвняння |
|
x |
2 |
|
|
|
x |
|
4 |
|
6 має безлiч коренiв. |
|||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
|
y |
x |
2 |
x |
4 |
|
8 |
|
|||||
|
6 |
|
|
y |
|
|
|
|
|
|
|
6 |
|
|
|
|
1 |
|
|
|
|
|
|
–2 |
0 |
1 |
4 |
х |
|
|
|
|
Рис. 38 |
|
|
|
|
|
|
Вiдповiдь. |
|
|
2; 4 . |
|||||||||
|
|
|||||||||||
в) |
|
x 2 |
|
|
|
x |
|
|
4 |
|
2. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання
Знайдемо абсциси точок перетину графiкiв функцiй y 
 x
x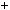 2
2
 x 4 та y
x 4 та y  2 (рис. 39).
2 (рис. 39).
|
у |
|
y |
x |
2 |
x |
4 |
|
8 |
|
|||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
2 |
|
|
y |
2 |
|
|
–2 |
0 |
1 |
4 |
х |
|
|
|
|
Рис. 39 |
|
|
|
|
|
|
Графiки функцiй y |
|
x |
2 |
|
|
x |
|
4 |
та y 2 не мають спiльних то |
|||||||
|
|
|
|
|||||||||||||
чок, отже, рiвняння |
|
x |
2 |
|
|
|
x |
|
4 |
|
|
2 коренiв не має. |
||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||
Вiдповiдь. Коренiв немає. |
|
|
|
|
|
|
|
|
||||||||
Роздiл ІІ. Функцiї та графiки |
|
|
|
|
|
|
|
|
|
63 |
|||||
Приклади рiвнянь, якi мають безлiч коренiв: |
|
|
|
|
|
||||||||||
а) x 1 |
x |
2 |
3; |
|
|
|
б) x |
1 |
x |
2 |
3. |
|
|
|
|
Розв’язання цих рiвнянь показано на рисунку 40. |
|
|
|
|
|||||||||||
|
у |
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
y |
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
–2 |
|
0 |
1 |
|
х |
|
|
–2 |
0 |
1 |
|
|
х |
|
|
|
|
|
y |
x 1 |
x |
2 |
y |
3 |
|
|
y |
x |
1 |
x |
2 |
|
–3 |
|
|
|
|
|
–3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
а) |
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
Рис. 40 |
|
|
|
|
|
|
|
|
|
Вiдповiдь. |
; |
2 . |
|
|
Вiдповiдь. 1; |
|
. |
|
|
|
|||||
Приклади рiвнянь, якi не мають коренiв: |
|
|
|
|
|
|
|||||||||
а) x 1 |
x |
2 |
5; |
|
|
|
б) x |
1 |
x |
2 |
4. |
|
|
|
|
Розв’язання цих рiвнянь показано на рисункy 41. |
|
|
|
|
|||||||||||
|
у |
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
y |
5 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
–2 |
|
0 |
1 |
|
х |
|
|
–2 |
0 |
1 |
|
|
х |
|
|
|
–3 |
y |
x 1 |
x |
2 |
|
|
|
–3 |
y |
x |
1 |
x |
2 |
|
|
|
|
|
|
y |
4 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
–4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
Рис. 41 |
|
|
|
|
|
|
|
|
|
Вiдповiдь. Коренiв немає. |
|
Вiдповiдь. Коренiв немає. |
|
||||||||||||
Приклад рiвняння, яке має один корiнь: x |
1 |
x |
2 |
1. |
|
|
|||||||||
Розв’язання цього рiвняння показано на рисунку 42.

64 |
Матерiали для факультативних занять, спецкурсiв, гурткiв. Математика 5–7 |
Роздiл ІІ. Функцiї та графiки |
65 |
у |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
y |
1 |
|
|
|
|
|
|
|
|
–2 –1 |
0 |
1 |
|
|
|
х |
|
|
y |
x |
1 |
x |
2 |
–3 |
|
|
|
|
|
|
Рис. 42 |
|
|
|
|
|
|
Вiдповiдь. –1.
Завдання для самостiйного розв’язування
Розв’яжiть рiвняння, використовуючи графiчний спосiб:
2.35. а) |
|
x |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
7; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
2 |
|
|
|
|
|
|
|
x |
|
|
|
5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) |
|
|
|
|
|
x |
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
|
|
|
|
|
|
|
x |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
д) |
|
|
|
|
|
x |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е) |
|
|
|
5 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.36. а) |
|
2x |
|
|
|
|
|
3 |
|
|
5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
2x |
|
3 |
|
|
|
5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) |
|
2x |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
2.37. а) |
|
x |
|
|
|
|
|
|
|
|
|
|
1 |
2; |
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
x |
1 |
|
3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
1 |
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x; |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.38. а) |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2; |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
1; |
|
|
|
|
|
г) |
|
|
1 |
|
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2.39. а) |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
1 |
|
|
5; |
|
б) |
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
1 |
|
3; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
1; |
|
|
|
|
г) |
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
0. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.40. а) |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
1 |
|
|
|
|
5; |
|
б) |
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
|
|
|
|
|
|
3; |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3; |
|
|
|
г) |
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
4; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
д) |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
1 |
|
|
|
|
|
|
|
1; |
|
|
|
|
е) |
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
|
|
|
0. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.41. а) |
|
x |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
4 |
|
0; |
б) |
|
x |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
6; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) |
|
x |
|
|
|
|
4 |
|
|
|
x |
|
|
|
|
x 4 |
|
|
|
2; |
г) |
|
x |
|
4 |
|
|
|
x |
|
|
|
|
|
x 4 |
|
|
|
|
4. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Робота для самоперевiрки
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Варiант 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Варiант 2 |
|||||||||||||||||||||||
Розв’яжiть графiчно рiвняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
а) |
|
|
|
|
|
x |
4 |
|
|
|
|
6; |
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
x |
|
|
|
|
4 |
|
|
|
6; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
б) |
|
|
|
2x |
|
|
5 |
|
|
7; |
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
2x |
5 |
|
7; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
в) |
|
|
|
|
|
1 |
|
|
|
|
|
|
2; |
|
|
|
|
|
|
|
1 |
|
|
|
|
2; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
г) |
|
|
|
x |
3 |
|
|
|
|
|
|
|
x |
1 |
|
|
|
6; |
|
|
г) |
|
|
|
x |
|
|
|
1 |
|
|
|
|
x |
|
|
|
3 |
|
6; |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
д) |
|
x |
3 |
|
|
|
|
|
x |
|
3 |
|
|
|
|
6; |
|
|
д) |
|
x |
|
3 |
|
|
x |
3 |
|
|
|
|
|
6; |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
е)* |
|
x |
1 |
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
1 |
|
0 |
е)* |
|
x |
2 |
|
|
|
x |
|
|
|
|
|
x |
|
2 |
|
0 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольна робота з теми «Побудова графіків функцій, що містять модулі»
Варiант 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
1. Побудуйте графiк функцiї: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) y |
|
|
3x |
|
|
|
|
|
|
|
6 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) y |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) y |
|
2x 1 |
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
1; |
|
|
|
|
|
|
г) y |
|
1 |
|
|
|
x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
x 1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Розв’яжiть графiчно рiвняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) |
|
|
|
5x |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
8; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
2x |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1; |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) |
|
|
|
x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
|
|
|
x |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
6; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
д) |
|
x |
|
3 |
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
5; |
|
|
|
|
|
|
|
|
|
е) |
|
x |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
1; |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ж)* |
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
|
|
4 |
|
|
|
|
|
x |
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Варiант 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
1. Побудуйте графiк функцiї: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) y |
|
2x 4 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) y |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
x |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) y |
|
3x 6 |
|
|
|
|
|
|
3x |
|
6 |
|
; |
|
|
|
|
|
|
г) y |
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||
2. Розв’яжiть графiчно рiвняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) |
|
4x |
|
1 |
|
5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
2x 4 |
|
1 |
|
|
|
x; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в) |
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
2 |
|
|
5; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
д) |
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
|
|
|
|
4; |
|
|
|
|
|
|
|
|
|
е) |
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
|
|
6; |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ж)* |
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
3 |
|
|
6 |
|
|
|
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
66Матерiали для факультативних занять, спецкурсiв, гурткiв. Математика 5–7
§4. ФУНКЦІЇ y 
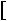 x
x ТА y
ТА y 
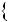 x
x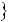
1. Цiла i дробова частина числа
Кожне дробове число можна подати у виглядi суми двох додан кiв, один iз яких — цiле число, а другий — невiд’ємний правильний дріб, тобто для кожного дробового числа можна вказати його цілу і дробову частину.
Наприклад, для числа 5,605 число 5 є цiлою частиною, а число 0,605 — дробовою частиною. Записують це так:
5605,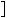
 5,
5, 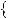 5605,
5605,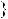
 0,605.
0,605.
Число 5,605 знаходиться мiж числами 5 i 6, якi є найближчими цiлими числами до 5,605. 5  5605,
5605,  6.
6.
Крiм того, число 5 — найближче цiле число, яке не перевищує число 5,605. Зазначимо, що 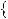 5605,
5605,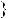
 5605, 5
5605, 5 0,605.
0,605.
Означення. Цiлою частиною числа a (позначення a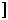 ) найближ че до a цiле число, яке не перевищує a.
) найближ че до a цiле число, яке не перевищує a.
Приклади:
1)7,31  7, оскiльки 7
7, оскiльки 7 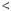 7,31
7,31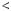 8;
8;
2)0,51  0, оскiльки 0
0, оскiльки 0 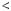 0,51
0,51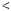 1;
1;
3) |
|
531, |
|
6, оскiльки |
|
6 |
|
531, |
|
5 (рис. 43). |
|
|||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
–6 |
0 |
|
|
7 |
|
x |
||||||
|
|
|
|
|
|
|
|
0,51 |
|
|
|
|||||
|
|
|
|
–5,31 |
|
7,31 |
|
|||||||||
Рис. 43
Означення. Дробовою частиною числа a (позначення 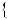 a ) нази
a ) нази
вається рiзниця мiж самим числом a i його цiлою частиною:
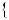 a
a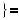 a a
a a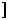 . Приклади:
. Приклади:
1)7,31  7,31 7
7,31 7  0,31;
0,31;
2)0,51  0,51 0
0,51 0  0,51;
0,51;
3)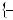 531,
531, 
 531,
531, 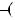
 6
6  0,69;
0,69;
4)5  5 5
5 5 0.
0.
Із означення дробової частини числа випливає її властивiсть: 0 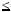 a
a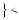 1.
1.
Роздiл ІІ. Функцiї та графiки |
67 |
Завдання для самостiйного розв’язування
2.42. Укажiть цiлу й дробову частини числа:
а) 1,571; |
б) 10,25; |
в) 0,051; |
г) 7; |
д) –7; |
е) –8,35; |
ж) –10,001; |
з) –0,05. |
2.43. Знайдiть значення виразу та вкажiть його цiлу й дробову час
тини: |
|
|
|
|
|
|
|
|
|
|
||||
а) 3 17, |
|
2; |
|
|
б) |
|
|
3 2,3 |
2; |
|||||
|
|
|
||||||||||||
в) 37, 2,1 |
35,; |
|
г) |
|
|
2,4 |
|
55, 10; |
||||||
|
|
|||||||||||||
д) |
|
17, |
|
34, |
|
53,. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
2. Функцiя y |
|
x та деякi її властивостi |
||||||||||||
Цiла частина числа визначена для всiх чисел, оскiльки будь якому числу можна поставити у вiдповiднiсть його цiлу частину. Та
ким чином, y |
|
x — функцiя, областю визначення якої є всi числа: |
|||||||||||||||||||||||||||
D x |
|
|
|
|
; |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Розглянемо значення функцiї y x для конкретних значень ар |
|||||||||||||||||||||||||||||
гументу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
За означенням цiлої частини числа: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
якщо 0 |
|
x |
|
1, то |
x |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
якщо 1 |
|
x |
|
2, то |
x |
1 i так далi. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Якщо |
|
|
1 |
x |
|
0, то |
x |
|
|
|
1; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
якщо |
|
2 |
x |
|
|
1, то |
x |
|
|
|
|
2 i так далi. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
У загальному виглядi, маємо: якщо m |
x |
m |
1, то |
x |
m, де |
||||||||||||||||||||||||
m — цiле число. Отже, область значень функцiї y |
|
x є всi цiлi |
|||||||||||||||||||||||||||
числа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Враховуючи цi вiдомостi по |
|
|
|
|
у |
|
|
|
|
|
|||||||||||||||||||
будуємо графiк функцiї |
|
y x |
3 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
(рис. 44). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Побудувати |
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Приклади. |
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
графiк функцiї: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
||||||||||
|
|
|
|
|
|
–3 –2 –1 |
|
|
0 |
1 |
2 |
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
а) y 2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
||||||
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
–3 |
|
|
|
|
|
|||||||||||
Ордината |
кожної |
iз |
точок |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
графiка функцiї y |
2 x |
вдвiчi |
Рис. 44 |
|
|
|
|
||||||||||||||||||||||
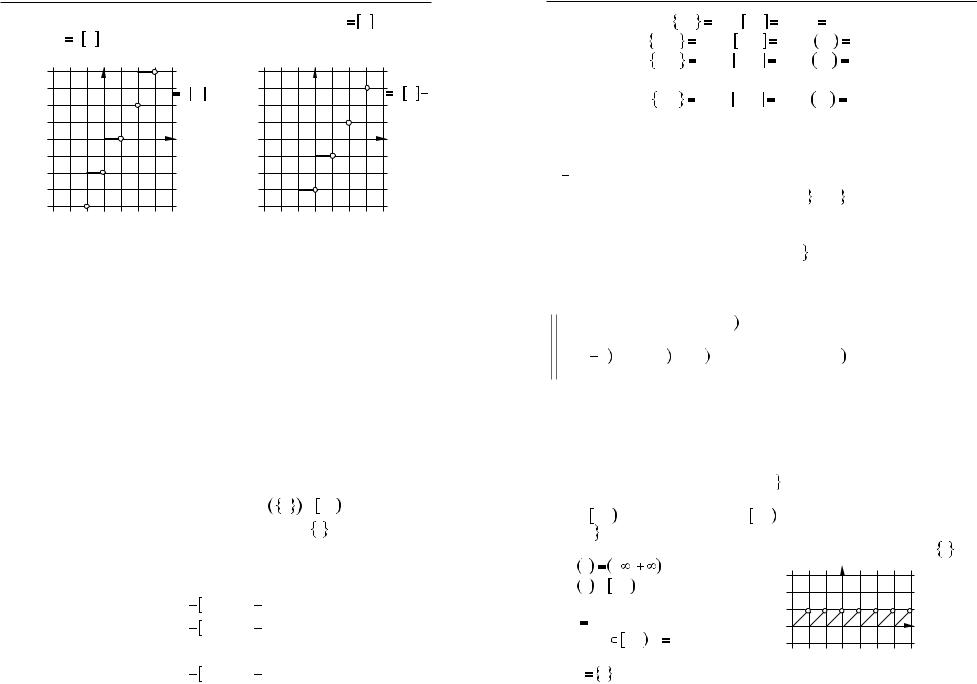
68 Матерiали для факультативних занять, спецкурсiв, гурткiв. Математика 5–7
бiльша за |
вiдповiдну |
ординату |
графiка функцiї |
y |
x . Графiк |
|||
функцiї y |
2 x зображений на рисунку 45. |
|
|
|
||||
|
4 |
у |
|
|
у |
|
|
|
|
|
|
у |
2 х |
3 |
|
у |
2 х 1 |
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
–3 –2 –1 |
0 1 2 |
3 |
х |
–3 –2 –1 0 |
1 |
2 3 |
х |
|
|
|
|
|
|
–1 |
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
–4 |
|
|
–3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 45 |
|
|
Рис. 46 |
|
|
||
б) y  2
2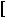 x
x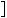
 1.
1.
Розв’язання
Ордината кожної точки графiка функцiї y  2
2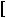 x
x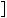
 1 на одиницю менша за вiдповiдну ординату точки графiка функцiї y
1 на одиницю менша за вiдповiдну ординату точки графiка функцiї y  2
2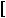 x
x . Графiк функцiї y
. Графiк функцiї y  2
2 x
x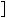
 1 зображений на рисунку 46.
1 зображений на рисунку 46.
3. Функцiя y 
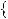 x
x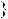 та її властивостi
та її властивостi
Дробова частина числа визначена для всiх чисел, оскiльки кож ному числу можна поставити у вiдповiднiсть його дробову частину. Таким чином, y 
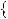 x
x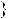 — функцiя, областю визначення якої є всi чис ла: D
— функцiя, областю визначення якої є всi чис ла: D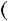
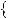 x
x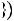

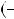
 ;
;
 .
.
Як було зазначено ранiше для дробової частини будь якого чис ла, виконується нерiвнiсть: 0 
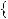 x
x
 1.
1.
Отже, область значень цiєї функцiї: E x  0;1 .
0;1 .
Розглянемо ще одну властивiсть функцiї y  x .
x .
Нехай аргумент x набуває таких значень: 5,7; 4,7; 3,7; 2,7; 1,7; 0,7; –0,3; –1,3; –2,3; –3,3; –4,3.
Обчислимо дробову частину кожного з цих чисел.
 57,
57,
 57, 57,
57, 57,
 57, 5
57, 5 0,7;
0,7;
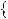 47,
47,
 47, 47,
47, 47,
 47, 4
47, 4 0,7;
0,7;
...
 17,
17,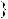
 17, 17,
17, 17,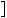
 17, 1
17, 1 0,7;
0,7;
Роздiл ІІ. Функцiї та графiки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
69 |
|||||||
0,7 |
|
0,7 |
|
|
|
|
|
|
0,7 |
|
|
0,7 |
|
|
|
|
0 |
|
0,7; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
0,3 |
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
1 |
0,7; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
13, |
|
|
|
|
13, |
|
|
|
|
|
|
|
|
|
13, |
|
|
|
|
13, |
|
|
|
|
|
|
|
|
|
2 |
0,7; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
43, |
|
|
43, |
|
|
|
|
|
|
|
43, |
|
|
|
43, |
|
|
|
|
|
|
|
|
5 |
0,7. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Помiтимо, що дробовi частини всiх цих чисел рiвнi.
Можна зробити висновок, що числа, якi вiдрiзняються одне вiд одного на цiле число, мають рiвнi дробовi частини. Тобто, якщо x2 x1 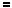 m, де m — цiле число, то
m, де m — цiле число, то
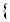 x2
x2
 x1
x1 або
або  x
x m
m 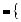 x . (*) Із розглянутого вище прикладу випливає, що найменше додатне
x . (*) Із розглянутого вище прикладу випливає, що найменше додатне
число, для якого при всiх x виконується рiвнiсть (*), дорiвнює 1. Кажуть, що значення функцiї y x повторюються з перiодом
x повторюються з перiодом
T 1.
1.
Означення перiодичної функцiї
Якщо для функцiї y f
f x iснує таке додатне число T, що для всiх x iз областi визначення цiєї функцiї виконується рiвнiсть f
x iснує таке додатне число T, що для всiх x iз областi визначення цiєї функцiї виконується рiвнiсть f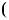 x T
x T  f
f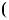 x
x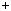 T
T  f
f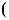 x , то функцiя y
x , то функцiя y f
f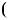 x називається перiо дичною, а число T називається її перiодом.
x називається перiо дичною, а число T називається її перiодом.
Слiд зауважити, що в природi iснує багато перiодичних про цесiв: змiна дня i ночi, змiна пiр року, рух небесних тiл за орбитами тощо.
У математицi бiльшiсть перiодичних процесiв описується за до помогою тригонометричних функцiй.
Повертаємось до функцiї y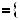 x . Вона перiодична з перiодом T
x . Вона перiодична з перiодом T  1. Тому достатньо дослiдити її поведiнку тiльки для x iз про мiжку 0; 1 . Вiдомо, що при x
1. Тому достатньо дослiдити її поведiнку тiльки для x iз про мiжку 0; 1 . Вiдомо, що при x 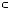 0; 1 цiла частина x дорiвнює нулю, тому
0; 1 цiла частина x дорiвнює нулю, тому 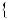 x
x  x.
x.
Таким чином, ми дiстали повне дослiдження функцiї y x .
x .
1) D y |
|
; . |
у |
|
|||
|
|
|
2) E y  0; 1 .
0; 1 .
3) |
Функцiя перiодична, |
1 |
||
|
T |
1. |
|
|
|
|
–3 –2 –1 0 1 2 3 х |
||
4) |
При x |
0; 1 y x. |
||
|
Побудуємо графiк фун |
|
||
кцiї y |
x |
(рис. 47). |
Рис. 47 |
|
|
|
|
|
|
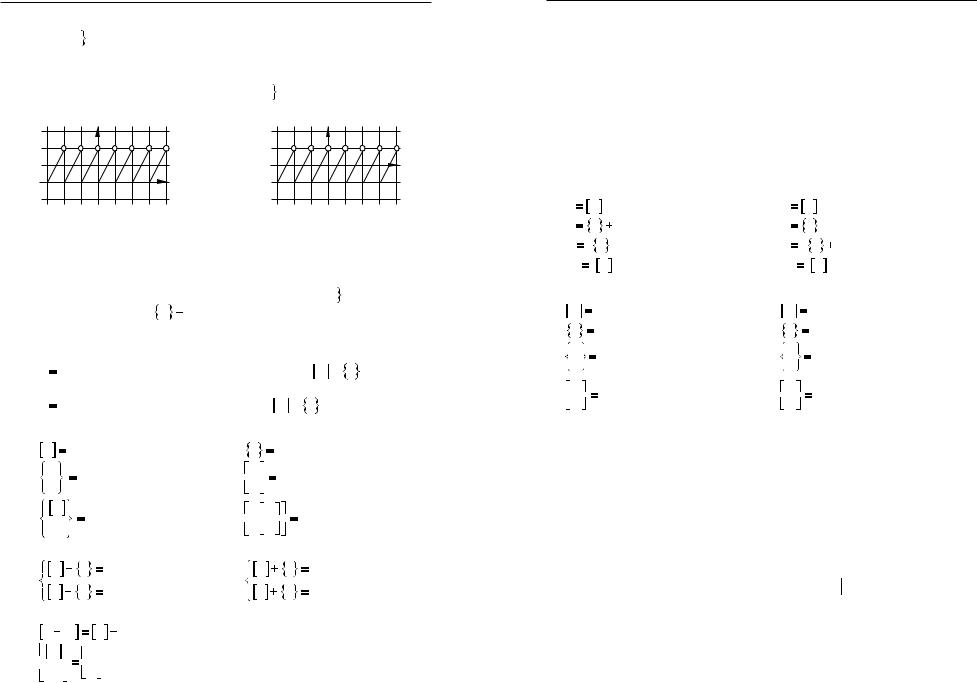
70 |
Матерiали для факультативних занять, спецкурсiв, гурткiв. Математика 5–7 |
Приклади. Побудувати графiк функцiї: а) y  2
2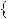 x .
x .
Розв’язання
Ординати всiх точок графiка функцiї y  2
2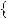 x
x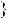 вдвiчi бiльшi за вiдповiднi ординати графiка функцiї y
вдвiчi бiльшi за вiдповiднi ординати графiка функцiї y 
 x . Графiк функцiї y
x . Графiк функцiї y  2
2 x
x зображений на рисунку 48.
зображений на рисунку 48.
|
у |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
–3 –2 –1 |
0 |
1 |
2 |
3 |
х |
Рис. 48 |
|
|
|
||
|
у |
|
|
|
|
1 |
|
|
|
–3 –2 –1 0 |
1 |
2 |
3 |
х |
–1 |
|
|
|
|
Рис. 49 |
|
|
|
|
б) y  2
2 x
x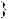
 1.
1.
Розв’язання
Ордината кожної точки графiка функцiї y  2
2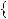 x
x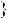
 1 на одиницю менша за вiдповiдну ординату точки графiка y
1 на одиницю менша за вiдповiдну ординату точки графiка y  2
2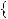 x .
x .
Графiк функцiї y  2 x 1 зображений на рисунку 49.
2 x 1 зображений на рисунку 49.
Завдання для самостiйного розв’язування
2.44. x |
1 |
, де n — натуральне число. Знайдiть x i x . |
||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2.45. x |
1 |
|
, де m — цiле число. Знайдiть |
x i |
x . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2.46. Розв’яжiть рiвняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
а) |
x |
3; |
|
|
|
|
|
|
|
|
б) |
x |
|
0,2; |
|
|||||||||||||||||||
в) |
|
x |
|
|
|
|
|
|
|
|
0,2; |
г) |
|
|
|
x |
|
2; |
|
|||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
д) |
|
x |
|
|
0; |
|
|
|
е) |
|
|
|
1 |
|
|
x |
|
|
|
|
|
1. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
||
2.47. Розв’яжiть систему рiвнянь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
а) |
|
|
x |
|
|
|
|
|
|
|
y |
2,3, |
б) |
|
x |
|
|
|
|
|
y |
2,3, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
x |
11,; |
|
y |
|
|
|
|
x |
11,. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2.48. Доведiть, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
а) |
x m x |
m, де m — цiле число; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
б) |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
, де n — натуральне число. |
|
|||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Роздiл ІІ. Функцiї та графiки |
|
|
|
|
|
|
|
|
|
|
|
71 |
||||||||||||||||||
|
|
|
Робота для самоперевiрки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Варiант 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Варiант 2 |
1. Знайдiть цiлу й дробову частини числа: |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
а) –7; |
|
|
|
|
|
|
|
|
|
|
а) –11; |
|
|
|
|
|||||||||||||||
б) 99,9; |
|
|
|
б) 101,99; |
|
|
|
|
||||||||||||||||||||||
в) –51,33; |
|
|
|
в) –47,28; |
|
|
|
|
||||||||||||||||||||||
г) |
|
|
32 |
1 |
|
|
|
|
|
|
|
|
г) |
|
|
304 |
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||
2. Побудуйте графiк функцiї: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
а) y |
|
x |
|
|
2; |
а) y |
|
|
x |
1; |
|
|||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
б) y |
|
x |
1; |
б) y |
|
|
x |
|
2; |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
в) y |
3 x |
|
|
1; |
в) y |
|
|
3 x |
1; |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
г)* y |
|
|
|
x |
|
1 |
г)* y |
|
|
|
x |
|
|
|
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3. Розв’яжiть рiвняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
а) |
|
x |
|
|
2; |
|
|
|
а) |
|
x |
13; |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
б) |
|
x |
0,1; |
|
б) |
|
x |
0,3; |
|
|
||||||||||||||||||||
в) |
|
|
x |
|
0; |
|
|
|
|
в) |
|
|
x |
0; |
|
|
|
|
||||||||||||
3 |
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
г) |
|
|
|
x |
|
1 |
|
|
|
|
г) |
|
|
|
x |
|
|
1 |
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 5. ПЕРЕТВОРЕННЯ ГРАФІКІВ ФУНКЦІЙ
Графiки деяких функцiй можна будувати, використовуючи гра фiк функцiї y  f
f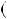 x
x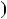 . Розглянемо способи побудови графiкiв деяких функцiй.
. Розглянемо способи побудови графiкiв деяких функцiй.
1. Побудова графiка функцiї виду y  f
f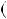 x
x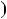
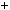 A
A
Ми вмiємо будувати графiк функцiї y 
 x (на рисунках 50–57 його зображено пунктиром).
x (на рисунках 50–57 його зображено пунктиром).
Розглянемо способи використання цього графiка для побудови графiкiв деяких iнших функцiй.
Приклади. Побудувати графiк функцiї: а) y 
 x
x
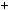 3.
3.
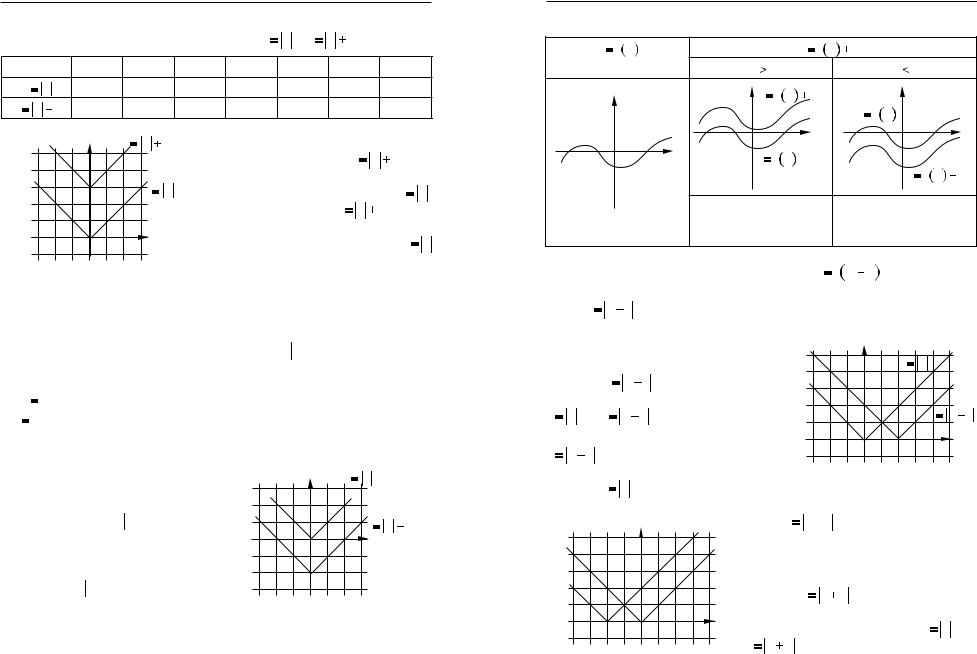
72 |
|
Матерiали для факультативних занять, спецкурсiв, гурткiв. Математика 5–7 |
|||||||||||||
|
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Складемо таблицю значень функцiй y |
x i y |
x |
|
3. |
|
|
|
|||||||
|
x |
|
–3 |
|
–2 |
|
–1 |
0 |
1 |
|
|
2 |
|
3 |
|
|
y |
x |
3 |
|
2 |
|
1 |
0 |
1 |
|
|
2 |
|
3 |
|
y |
x |
3 |
6 |
|
5 |
|
4 |
3 |
4 |
|
|
5 |
|
6 |
|
|
|
|
у |
y |
x |
3 |
Помiчаємо, що ордината кожної |
||||||||
|
|
|
|
|
|
точки графiка функцiї y |
x |
3 на 3 |
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
одиницi бiльша за вiдповiдну орди |
||||||||
|
|
|
3 |
|
y |
x |
нату |
точки |
графiка |
функцiї |
y |
x, |
|||
|
|
|
|
|
|
|
тому графiк функцiї y |
x |
3 можна |
||||||
|
|
|
1 |
|
|
|
здобути за допомогою паралельного |
||||||||
|
|
–2 |
0 |
2 |
х |
|
перенесення |
графiка |
функцiї |
y |
x |
||||
|
|
|
вздовж осi OY на 3 одиницi вгору |
||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
Рис. 50 |
|
|
|
(рис. 50). |
|
|
|
|
|
|
|
|
б) y 
 x
x
 2.
2.
Розв’язання
Складемо таблицю значень функцiй y 
 x i y
x i y 
 x
x
 2.
2.
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
|
|
x |
|
|
|
3 |
2 |
1 |
0 |
1 |
2 |
3 |
||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y |
|
x |
|
|
|
2 |
1 |
0 |
–1 |
–2 |
–1 |
0 |
1 |
|||
|
|
|||||||||||||||
|
|
|
||||||||||||||
Помiчаємо, що ордината кожної точки графiка функцiї y 
 x
x
 2 на 2 одиницi менша за вiдповiдну ординату точки гра фiка функцiї y
2 на 2 одиницi менша за вiдповiдну ординату точки гра фiка функцiї y 
 x, тому гра фiк функцiї y
x, тому гра фiк функцiї y 
 x
x
 2 можна здобути за допомогою пара лельного перенесення графiка функцiї y
2 можна здобути за допомогою пара лельного перенесення графiка функцiї y 
 x вздовж осi OY на 2 одиницi вниз (рис. 51).
x вздовж осi OY на 2 одиницi вниз (рис. 51).
Висновок, який можна зро бити, розглянувши цi прикла ди, вiдображено в таблицi 1.
|
у |
y |
x |
|
|
|
|
|
|
|
|
|
1 |
|
y |
x |
2 |
–2 |
0 |
2 |
х |
|
|
|
–2 |
|
|
|
|
|
Рис. 51 |
|
|
|
|
Роздiл ІІ. Функцiї та графiки |
|
|
|
|
|
|
|
|
|
|
|
|
73 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 1 |
||
|
|
y |
f x |
|
|
|
|
|
|
y |
f x |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
0 |
|
|
|
|
|
|
|
A |
0 |
|
|
|
|
у |
|
|
|
|
у y |
f x |
|
A |
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
f x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
|
|
х |
|
|
|
|
|
0 |
|
х |
|
|
|
|
0 |
|
х |
|
y |
f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
f x |
A |
|
|
|
|
|
|
|
Паралельне перене |
|
|
Паралельне перене |
|
|||||||||
|
|
|
|
|
|
сення вздовж осi OY |
|
сення вздовж осi OY |
|||||||||||
|
|
|
|
|
|
вгору |
|
|
|
|
|
|
вниз |
|
|
|
|
|
|
|
2. Побудова графiка функцiї виду y |
f |
x |
a |
|
|
|
|
|||||||||||
|
Приклади. Побудувати графiк функцiї: |
|
|
|
|
|
|
|
|
||||||||||
|
а) y |
x |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Скористаємось результатом вико |
|
|
|
|
|
у |
|
y |
x |
|
|
|||||||
нання |
завдання |
побудови |
графiка |
|
|
|
|
|
|
|
|
|
|||||||
функцiї y |
x |
2 . Зобразимо в однiй |
|
|
|
|
|
|
|
|
|
|
|
||||||
системi координат графiки функцiй |
|
|
|
|
|
3 |
|
|
|
|
|
||||||||
y |
x та y |
x 2 (рис. 52). |
|
|
|
|
|
|
|
1 |
|
|
y |
x |
2 |
||||
|
Помiчаємо, |
що |
графiк |
функцiї |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
–2 |
|
0 |
2 |
|
х |
||||||||||
y |
x 2 можна здобути за допомогою |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
паралельного |
перенесення |
графiка |
|
|
|
|
|
Рис. 52 |
|
|
|
|
|||||||
функцiї y |
x вздовж осi OX на 2 оди |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ницi праворуч. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
у |
|
|
|
|
б) y |
x |
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Скористаємось |
результатом |
ви |
|||||||||
|
|
|
|
|
|
|
конання завдання побудови графiка |
||||||||||||
|
|
|
|
2 |
|
|
функцiї y |
x |
2 . |
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
Зобразимо в однiй системi коор |
|||||||||||
|
|
–2 –1 |
0 |
|
х |
динат |
графiки |
функцiй |
y |
x |
та |
||||||||
|
|
|
|
|
|
|
y |
x |
2 |
(рис. 53). |
|
|
|
|
|
||||
|
|
|
Рис. 53 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
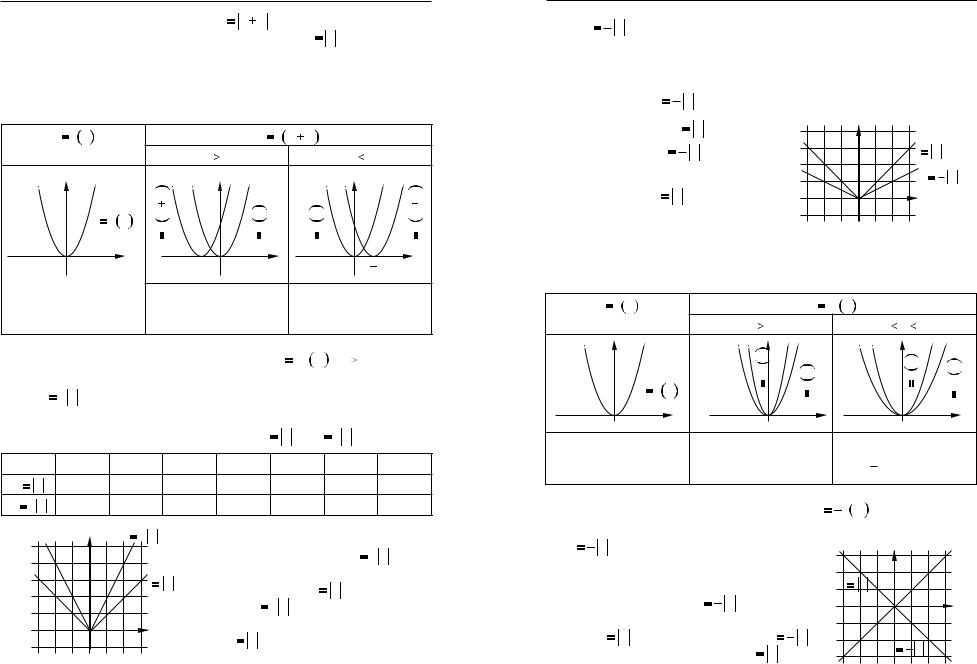
74 |
Матеріали для факультативних занять, спецкурсів, гуртків. Математика 5–7 |
||||||||||||
|
Помiчаємо, що графiк функцiї y |
x |
2 можна здобути за допомо |
||||||||||
гою паралельного перенесення графiка функцiї y |
x вздовж осi OX |
||||||||||||
на 2 одиницi лiворуч. |
|
|
|
|
|
|
|
|
|
|
|||
|
Висновок, який можна зробити, розглянувши цi приклади, |
||||||||||||
вiдображено в таблицi 2. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 2 |
|
|
y |
f x |
|
|
|
|
y |
f x |
a |
|
|
|
|
|
|
|
|
a |
0 |
|
|
|
|
|
a |
0 |
|
|
у |
|
|
a |
у |
|
|
|
|
|
у |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y |
f x |
x |
|
|
x |
|
|
x |
|
|
x |
|
|
f |
|
|
f |
|
|
f |
|
|
f |
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y |
|
|
y |
|
|
y |
|
|
y |
|
|
0 |
х |
–a |
0 |
|
х |
|
|
|
|
0 a |
х |
|
|
|
|
Паралельне |
|
|
|
Паралельне |
|
||||
|
|
|
|
перенесення вздовж |
|
перенесення вздовж |
|||||||
|
|
|
|
осi OX лiворуч |
|
|
|
осi OX праворуч |
|
||||
|
3. Побудова графiка функцiй виду y |
|
kf x |
(k |
0) |
|
|||||||
|
Приклади. Побудувати графiк функцiї: |
|
|
|
|
|
|||||||
|
а) y |
2 x. |
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання |
|
|
|
|
|
|
|
|
|
|
||
|
Складемо таблицю значень функцiй y |
x та y |
2 x. |
|
|
||||||||
|
x |
|
–3 |
|
–2 |
|
–1 |
|
0 |
1 |
2 |
|
3 |
y |
x |
|
3 |
|
2 |
|
1 |
|
0 |
1 |
2 |
|
3 |
y |
2 x |
|
6 |
|
4 |
|
2 |
|
0 |
2 |
4 |
|
6 |
|
|
|
у |
y |
2 x |
|
|
Помiчаємо, що ордината кожної |
|||||
|
|
|
|
|
|
|
точки графiка функцiї y |
2 x удвiчi |
|||||
|
|
|
|
|
y |
x |
бiльша за ординату вiдповiдної точки |
||||||
|
|
|
3 |
|
графiка функцiї y |
x, тому графiк |
|||||||
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
функцiї y |
2 x можна здобути за до |
|||||
|
|
|
|
|
|
помогою розтягування графiка функ |
|||||||
|
|
|
|
|
|
|
|||||||
|
|
–2 |
0 |
2 |
х |
|
цiї |
y |
x |
вздовж |
осi |
OY |
удвiчi |
|
|
|
|
|
|
|
(рис. 54). |
|
|
|
|
||
|
|
|
Рис. 54 |
|
|
|
|
|
|
|
|
|
|
Розділ ІІ. Функції та графіки |
|
|
|
|
|
75 |
||
б) y |
1 x. |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Розв’язання |
|
|
|
|
|
|
|
|
За аналогiєю iз попереднiм прикладом, ордината кожної точки |
||||||||
графiка функцiї y |
1 x удвiчi менша за ординату вiдповiдної точки |
|||||||
|
|
2 |
|
|
|
|
|
|
графiка |
функцiї |
y |
x, |
тому |
у |
|
|
|
|
|
1 x |
|
|
|
|
||
графiк |
функцiї y |
можна |
3 |
|
y |
x |
||
|
|
2 |
|
|
|
|
|
1 x |
здобути за допомогою стискання |
1 |
|
y |
|||||
графiка функцiї y |
x вздовж осi |
|
|
|
2 |
|||
|
|
х |
|
|||||
OY удвiчi (рис. 55). |
|
|
–2 |
0 |
2 |
|
||
|
|
|
|
|
|
|
||
Висновок, який можна зро |
Рис. 55 |
|
|
|
||||
бити, розглянувши цi приклади, |
|
|
|
|||||
|
|
|
|
|||||
вiдображено в таблицi 3. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Таблиця 3 |
||
|
y |
f x |
|
|
|
y |
kf x |
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
0 |
k |
1 |
|
|
у |
|
|
kf x |
у |
|
|
|
|
|
у |
|
|
|
|
y |
f x |
|
f x |
|
|
|
|
f x |
|
kf x |
|
|
|
y |
|
y |
|
|
|
|
y |
|
y |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
х |
|
0 |
х |
|
|
|
|
0 |
|
х |
|
|
|
Розтягування вздовж |
Стискання вздовж осi |
|||||||||
|
|
|
осi OY в k разiв |
|
OY в |
1 |
разiв |
|
|
||||
|
|
|
|
|
|
|
k |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Побудова графiка функцiї виду y |
f |
x |
|
|
|
|
|
||||||
Приклад. Побудувати графiк функ |
|
|
|
|
|
|
|
||||||
цiї y |
x. |
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Легко помiтити, що ордината кожної |
y |
x |
|
1 |
|
|
|
||||||
точки графiка функцiї y |
x протилеж |
|
–2 |
|
|
0 |
2 |
х |
|||||
на до вiдповiдної ординати точки графiка |
|
|
|
||||||||||
функцiї y x , тому графiк функцiї y |
x |
|
|
|
y |
|
x |
|
|||||
симетричний графiку функцiї y |
x вiд |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
носно осi OX (рис. 56). |
|
|
|
|
|
|
Рис. 56 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
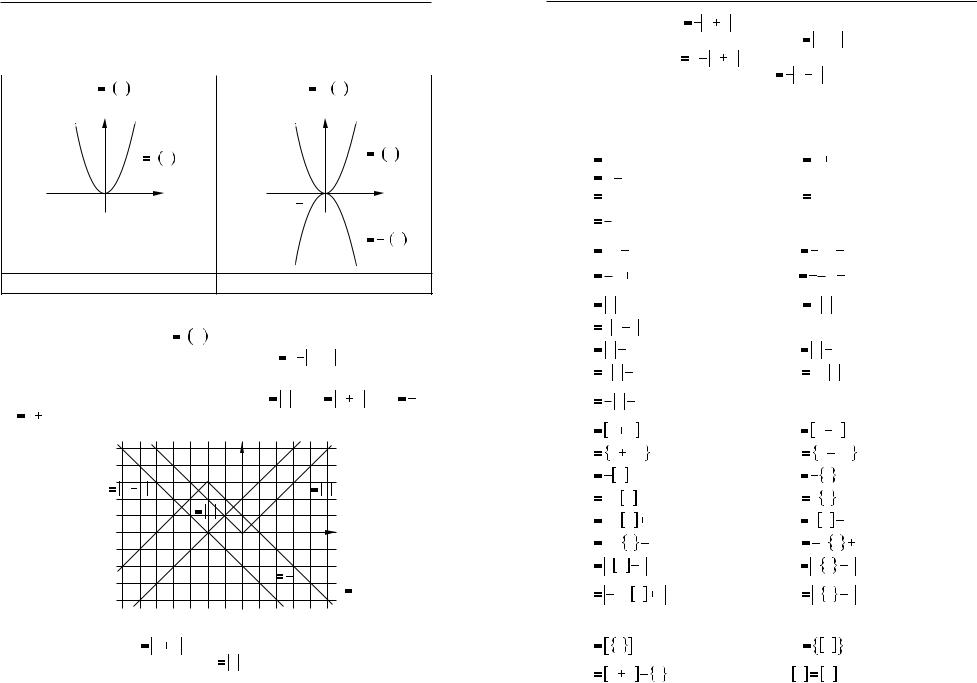
76 |
Матеріали для факультативних занять, спецкурсів, гуртків. Математика 5–7 |
Розділ ІІ. Функції та графіки |
77 |
Висновок, який можна зробити, розглянувши даний приклад, |
2) |
графiк функцiї y2 |
x 2 здобуто за допомогою осьової симетрiї |
||||||
вiдображено в таблицi 4. |
|
|
|
|
|
вiдносно осi OX графiка функцiї y1 |
x 2 ; |
||
|
|
|
Таблиця 4 |
3) |
графiк функцiї y |
3 x 2 здобуто за допомогою паралельного |
|||
|
|
|
|
|
|
перенесення графiка функцiї y2 |
x |
2 вздовж осi OY на 2 оди |
|
y f x |
y |
|
f x |
|
|
||||
|
|
ницi вгору. |
|
|
|
||||
|
|
|
|
|
|||||
у |
|
|
у |
|
Завдання для самостiйного розв’язування |
||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
f x |
|
2.49. Побудуйте графiки функцiй: |
|
|
|
|
|||
|
|
y |
f x |
|
|
|
|
|
|
|
|
|
1) а) y |
x; |
|
|
б) y |
x |
3; |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) y |
x 3. |
|
|
|
|
|
|
|
|
0 |
х |
|
|
|
|
|
|
a |
0 |
|
х |
|
2) а) y |
x; |
|
|
б) y |
3x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
f x |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) а) y |
2x |
3; |
|
б) y |
2x |
3; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Симетрiя вiдносно осi OX |
|
в) y |
1 x |
2; |
|
г) y |
1 x |
2. |
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) а) y |
x; |
|
|
б) y |
3 x; |
|
|
|
5. Застосування декiлькох перетворень |
|
|
|
|
в) y |
3 x |
1. |
|
|
|
|
|
|||||||||
|
до графiка функцiї y |
f |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
5) а) y |
x |
3; |
|
б) y |
x |
5; |
||||||
|
Приклад. Побудувати графiк функцiї y |
3 |
x |
2 . |
|
|
|
|
||||||||||||||
|
|
|
|
в) y |
3 x |
4; |
|
г) y |
15, x |
2,5; |
||||||||||||
|
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
Розглянемо |
допомiжнi |
функцiї |
y0 |
|
x, |
y1 |
x |
2 , |
y2 |
y1 , |
д) y |
6. |
|
|
|
|
|
||||
y3 |
3 y2 та їхнi графiки, що зображенi на рисунку 57. |
|
|
|
4 |
|
|
б) y x 2 ; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) а) y x 2 ; |
|
||||||
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
в) y |
x |
0,5 ; |
г) y |
x |
0,4 . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
y1 |
x |
2 |
|
|
3 |
|
|
y0 |
x |
|
|
|
7) а) y |
x ; |
|
б) y |
x ; |
|
|||
|
|
|
|
|
|
|
|
в) y |
15, x ; |
|
г) y |
3 x . |
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
y |
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
8) а) y |
0,5 x |
1; |
б) y |
3 x |
|
2; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
–5 –4 –3 –2 –1 |
0 1 |
2 |
3 |
|
х |
|
|
|
в) y |
2,5 x |
1; |
г) y |
2 x |
3. |
|||||
|
|
|
|
|
|
|
y2 |
|
y1 |
|
|
|
|
|
9) а) y |
2 x |
1; |
б) y |
2 x |
1; |
||
|
|
|
|
|
|
|
|
|
y3 |
3 |
y2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
в) y |
0,5 x |
1; |
г) y |
3 x |
4. |
|||||
|
|
|
|
|
Рис. 57 |
|
|
|
|
|
|
|
|
2.50. Побудуйте множину точок на координатнiй площинi: |
||||||||
1) Графiк функцiї y1 |
x 2 здобуто за допомогою паралельного пе |
а) y |
x |
; |
|
б) y |
x |
|
; |
|||||||||||||
|
ренесення графiка функцiї y |
x вздовж осi OX на 2 одиницi |
в) y |
x |
1 |
x ; |
г) y |
x . |
|
|||||||||||||
|
лiворуч; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

78 |
|
|
|
|
|
Матеріали для факультативних занять, спецкурсів, гуртків. Математика 5–7 |
||||||||||||||||||||||||||||||||||||||||||
|
Робота для самоперевiрки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Варiант 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Варiант 2 |
|||||||
1. Побудуйте графiк функцiї: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а) y |
|
|
x |
1 |
|
|
|
|
|
5; |
|
а) y |
|
|
x |
|
|
|
1 |
|
5; |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
б) y 5 |
|
2 |
|
x |
|
; |
|
|
|
б) y 3 |
|
2 |
|
x |
|
; |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
в) y |
3 x |
|
|
2; |
|
|
|
в) y |
3 x |
|
|
|
|
|
|
|
2; |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
г) y |
|
|
|
|
|
|
|
2 |
|
|
|
г) y |
|
|
3 x |
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||
|
3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2. Розв’яжiть рiвняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
а) |
x |
1 |
|
|
|
|
|
2; |
|
|
|
|
|
а) |
x |
|
|
1 |
|
|
|
3; |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
б) |
x |
|
0,5 |
|
|
1 |
|
|
|
б) |
x |
0,5 |
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Контрольна робота з теми «Функції y |
|
|
|
|
|
|
x та y x » |
||||||||||||||||||||||||||||||||||||||||
|
Варiант 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1. Побудуйте графiк функцiї: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
а) y |
2 |
|
|
|
|
|
|
|
x |
|
1; |
|
б) y |
|
|
2 x |
|
|
2; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
в) y |
|
|
|
|
|
x ; |
|
|
г) y |
|
|
|
x |
|
|
|
|
|
1 |
|
1. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. Розв’яжiть рiвняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
а) 3 x 1 2 x ; |
|
б) 3 x 1 2 x . |
|||||||||||||||||||||||||||||||||||||||||||||
3. Розв’яжiть графiчно рiвняння |
|
x |
|
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.* Укажiть усi значення параметра a, при яких рiвняння має ко
|
ренi: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) x |
|
3 a; |
б) x |
|
|
|
|
a |
|
|
1. |
||||||||||
|
|
|
||||||||||||||||||||
|
Варiант 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1. |
Побудуйте графiк функцiї: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
а) y 3 |
|
|
|
x 2 |
|
; |
б) y 3 x 3; |
||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
в) y |
|
|
2 x ; |
г) y |
|
|
x |
|
|
2 2. |
|||||||||||
|
|
|
|
|
||||||||||||||||||
2. |
Розв’яжiть рiвняння: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
а) 2 x |
|
2 3 x ; |
б) 2 x |
|
|
2 |
|
|
3 x . |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||
3. |
Розв’яжiть графiчно рiвняння |
x |
|
x |
|
1. |
||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.* Укажiть усi значення параметра a, при яких рiвняння має ко
ренi: |
|
а) x 2 a 0,1; |
б) x 0,2 a. |
Назва |
79 |
Роздiл ІІІ. СИСТЕМИ ДВОХ ЛІНІЙНИХ РІВНЯНЬ
ЗДВОМА ЗМІННИМИ
§1. СТАНДАРТНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ СИСТЕМИ ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ
1. Загальнi вiдомостi
Два лiнiйних рiвняння з двома змiнними, для яких треба знайти розв’язки, що задовольняють одночасно обидва рiвняння, назива ються системою двох лiнiйних рiвнянь з двома змiнними.
Записують систему рiвнянь, об’єднуючи їх фiгурною дужкою:
|
|
|
|
|
|
a11 x |
a12 y |
b1 , |
|
||||
|
|
|
|
|
|
a21 x |
a22 y |
b2 , |
|
||||
де a11 , a12 , a21 , a22 , b1 , b2 |
— заданi числа, x i y — змiннi. Наприклад, |
||||||||||||
2x |
|
|
3y |
5, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
у системi рiвнянь |
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
|
5y |
1. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
a11 |
2, a12 |
|
3, b1 |
5, |
|||||
|
|
|
|
|
|||||||||
|
|
|
|
a21 |
|
|
1, a22 |
|
5, b2 |
1. |
|||
|
|
|
|
|
|
|
|||||||
Розв’язком системи двох рiвнянь з двома змiнними називається впорядкована пара чисел, яка пiд час пiдстановки в систему пере творює кожне рiвняння в правильну числову рiвнiсть.
Наприклад, пара чисел 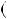 4; 1 є розв’язком системи рiвнянь
4; 1 є розв’язком системи рiвнянь
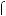 2x 3y
2x 3y  5,
5, 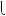
 x
x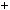 5y
5y  1.
1.
Дiйсно,
2x 3y  2
2 4 3
4 3 1
1 8 3
8 3 5, x
5, x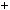 5y
5y 
 4
4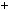 5
5 1
1 1.
1.
