4. Функция распределения и критерий

В режиме «Счёт с выводом гистограммы» были сделаны две серии измерений числа α-частиц. В первой серии измерительный интервал выбирался так, чтобы среднее число импульсов за интервал было примерно 23, во второй серии – примерно 50100. После этого с помощью управляющей программы результаты двух серий были записаны на дискету и обработаны в Excel. По формулам

и

были найдены среднее и среднеквадратичное отклонение. После полученные данные были аппроксимированы теоретическими распределениями Гаусса

и Пуассона

(,).

Для каждого из распределений была найдена

.

1 серия

,

.

Для распределения Пуассона . Для распределения Гаусса .

2 серия

,

.

Распределения Пуассона . Распределения Гаусса .

Потом мы убрали α-источник и сняли счетную характеристику при Δτ = 200 мс и N = 20:

Табл. 6. Счетная характеристика без α - частиц

U, kB	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2	2,1	2,2	2,3	2,4	2,5
x	0	0	0	0	0,1	0,1	1,1	7,6	36,8	400	2740	3150	3863,3	3876
SX	0	0	0	0	0,316	0,316	1,01	2,01	9,2	33,25	179,04	204,3	253	209,1

Рис. 6. Счётная характеристика детектора 2

Таким образом, оптимальное напряжение (видим из табл. 1) 1,6 кВ.

2. Анализ результатов измерений

   1. Обработка результатов

Активность источника находится по формуле

,

где – коэффициент Стьюдента. Подставив= 3316,, прии доверительной вероятности , при доверительной вероятности , получим для

N = 3000 35 шт/с

для

N = 3000 42 шт/с

Счетная характеристика детектора

Поэтому перед началом измерений необходимо снять счетную характеристику – зависимость загрузки (скорости счета) от напряжения.

Влияние числа измерений и интервала счета на точность определения среднего.

Из приведенных таблиц видно, что среднеквадратичная ошибка среднего S_x уменьшается с увеличением числа измерений и уменьшением интервала счета.

Табл. 7. ∆T=1000 mс						Табл. 8. ∆T=10mс
N	2	4	16	256		N	2	4	16	256
x	3316	3422,7	3370,5	3373.2		x	33,500	32,250	30,313	33,277
SN	73,539	61,348	40,223	55,951		SN	3,536	7,762	5,301	5,928
Sx	52,0	30,674	10,056	3,497		Sx	2,500	3,881	1,325	0,371

Построение и анализ гистограмм

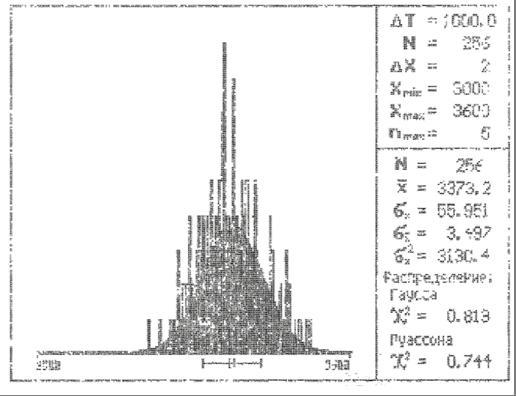
Рис. 7. Гистограмма для большого периода.

Рис. 8. Гистограмма с малым периодом

При установленном оптимальном напряжении питания ФЭУ (1.6 кВ) в режиме «Непосредственный счёт» был задан интервал времени отсчёта . Заполняя таблицу, было прослежено, как изменяются значения среднего, среднеквадратичного отклоненияи среднеквадратичной ошибки среднегопо мере увеличения числа измеренийв выборке. В таблице 2 приведены характерные значения,,. То же самое было проделано при.

Табл. 9. Зависимость точности среднего значения числа импульсов от размера выборки.

N					N
4	0,75	0,957	0,479		4	197	13,526	6,663
16	1,500	1,506	0,376		16	194,875	12,727	3,182
64	1,984	1,507	0,188		64	202,109	14,852	1,856

Для используемого α-источника: N=256, ∆Т=1с

57.76

24.6

В результате серии экспериментов для разных ∆Т и для разных N точность аппроксимации, полученной гистограммы распределения Гаусса, тем выше, чем больше N и чем ниже ∆Т. Теоретические распределения, тем точнее аппроксимируются на гистограмме, чем больше ширина бина (Δx)

Табл. 10. ∆Т=10, Δx =2				Табл. 11. ∆Т=1000, Δx =2
N	א			N	א
	Гаусса	Пуассона			Гаусса	Пуассона
2	0,313	2		2	0,426	0,489
4	0,950	4		4	0,581	0,601
16	0,515	16		16	0,896	0,429
256	0,696	256		256	0,819	0,744