
12.3 Оценка достоверности показателей регрессии
Выборочные показатели регрессии являются оценками соответствующих генеральных параметров и, как величины случайные, сопровождаются статистическими ошибками. Ошибку выборочного коэффициента регрессии Y по X определяют по формуле
 ,
()
,
()
а ошибку коэффициента регрессии X по Y – соответственно
 .
().
.
().
Достоверность
выборочного коэффициента регрессии
оценивается с помощью t-критерия
Стьюдента. Нулевую гипотезу отвергают
на принятом уровне значимости α
с
числом степеней свободы
 ,
если
,
если .
.
Если исходные данные сгруппированы в вариационные ряды, а их частоты распределяются по ячейкам корреляционной таблицы, ошибку коэффициентов регрессии определяют с учетом классовых интервалов по следующим формулам:
 ;
;
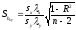 ()
()
Эмпирические уравнения регрессии также сопровождаются ошибками. Последние, обозначаемые символами Syx и Sxy, могут быть рассчитаны по формулам
 ;
;

или
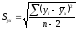 и
и ,
,
где
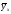 и
и – частные средние переменныхY
и X;
– частные средние переменныхY
и X;
 – число степеней свободы.
– число степеней свободы.
Значения
Sxy
и
Syx
также называют частными,
парциальными
или остаточными
средними квадратическими отклонениями.
Они описывают величину изменчивости
отдельных наблюдений по отношению к
линии регрессии, т.е. частными средними
 (или
(или ),
составляющим эту линию. ВеличинаSxy
или
Syx
позволяет судить насколько можно
ошибиться, пытаясь найти значение
признака y
или x
как значение частной средней, полученной
по уравнению регрессии.
),
составляющим эту линию. ВеличинаSxy
или
Syx
позволяет судить насколько можно
ошибиться, пытаясь найти значение
признака y
или x
как значение частной средней, полученной
по уравнению регрессии.
Случайная
вариация отдельных частных средних
 ,
принадлежащих линии регрессии, зависит
от величины остаточной вариации признакаY,
т.е. от Syx,
объема выборки n,
по которой оценивали регрессионную
связь, и от того, насколько далеко от
средней
,
принадлежащих линии регрессии, зависит
от величины остаточной вариации признакаY,
т.е. от Syx,
объема выборки n,
по которой оценивали регрессионную
связь, и от того, насколько далеко от
средней
 отстоит значениеx,
для которого по уравнению регрессии
отстоит значениеx,
для которого по уравнению регрессии
 была найдена величина
была найдена величина .
Квадратическая ошибка частой средней
может быть получена по формуле
.
Квадратическая ошибка частой средней
может быть получена по формуле
 ,
,
а доверительный интервал может быть задан выражением
 ,
,
где
t
зависит от числа степеней свободы
 и от принятого уровня значимостиα.
и от принятого уровня значимостиα.
Иногда практический интерес может представлять построение доверительного интервала для отдельных наблюдений, например если требуется очертить зону, включающую в себя определенный процент всех эмпирических наблюдений, располагающихся возле линии регрессии. В этом случае может быть использована формула квадратической ошибки отдельного наблюдения
 ,
,
а доверительный интервал будет иметь границы
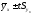 ,
,
где
t
зависит от числа степеней свободы
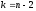 и от принятого уровня значимостиα..
Следует
заметить,
что
границы
доверительного интервала для разных
значений x
будут расширяться в той мере, в какой
эти значения будут отличаться от среднего
уровня x.
и от принятого уровня значимостиα..
Следует
заметить,
что
границы
доверительного интервала для разных
значений x
будут расширяться в той мере, в какой
эти значения будут отличаться от среднего
уровня x.
12.4 Выбор уравнений регрессии
Важной задачей в области регрессионного анализа является выбор уравнения, которое бы наилучшим образом описывало исследуемую закономерность. Обычно эту задачу решают следующим образом:
Эмпирический ряд регрессии или динамики, для которого подыскивают наилучшее корреляционное уравнение, изображают в виде точечного графика в системе прямоугольных координат. Если эмпирические точки располагаются на одной прямой или могут быть аппроксимированы прямой линией, зависимость между переменными величинами описывают уравнением линейной регрессии. В случае нелинейной зависимости подходящее уравнение подбирают на основании сравнения эмпирического графика с известными образцами кривых.
Графический анализ не гарантирует от возможных ошибок, особенно в тех случаях, когда главное направление регрессии, т,е. тренд сильно затушевывается колебаниями членов ряда. Поэтому дополнительно применяют аналитические способы проверки правильности выбора корреляционных уравнений.
Одним из них является применение принципов дисперсионного анализа. Неадекватность линии регрессии, найденной теоретическим способом по отношению к эмпирической линии, может быть описана суммой квадратов отклонений
 .
.
Здесь
 и
и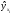 – эмпирические и теоретические условные
средние. Дисперсия неадекватности
регрессионной модели находят по формуле
– эмпирические и теоретические условные
средние. Дисперсия неадекватности
регрессионной модели находят по формуле
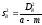
где
а
– число классовых интервалов, для
которых находили эмпирические средние
 ;m
– число параметров, определяемых в
регрессионной модели. Это количество
для прямолинейной регрессии равно двум,
для квадратической параболы – трем и
т.д.
;m
– число параметров, определяемых в
регрессионной модели. Это количество
для прямолинейной регрессии равно двум,
для квадратической параболы – трем и
т.д.
Случайная
вариация наблюдений yij
по отношению к условным средним
 ,
найденным эмпирически, определит
остаточную девиату
,
найденным эмпирически, определит
остаточную девиату
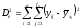
Остаточная дисперсия может быть получена по формуле

Сравнение
двух дисперсий осуществляют по F-критерию
Фишера по формуле
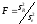 с числами степеней свободы
с числами степеней свободы и
и .
.
Если Fф превысит табличное значение Fst, найденное для kR и ke, а также выбранного уровня значимости α, то необходимо будет признать, что предположение об адекватности построенной теоретической регрессии следует отклонить и попытаться испытать иную модель. В противном случае (Fф < Fst) можно считать, что неадекватность проверяемой линии регрессии оказалась недоказанной, поэтому ее можно использовать.
В заключение необходимо отметить: уравнения регрессии позволяют прогнозировать возможные значения зависимой переменной на основании известных величин аргумента. При этом, однако, не следует экстраполировать регрессию за пределы проведенных опытов, так как она может менять свое направление. Область применения уравнений регрессии лучше ограничить теми данными, на которых получены эмпирические уравнения. Это предостережет исследователя от возможных ошибок.
