2.2 Нелинейная регрессия
Как уже было показано, наряду с линейными корреляциями в биологии встречаются и нелинейные корреляции между переменными величинами. Хорошо известна, например, логистическая закономерность возрастания численности популяции в замкнутой среде обитания. Эту и другие подобные зависимости могут быть описаны соответствующими корреляционными уравнениями, формулами или выражены в виде эмпирических или теоретических построенных линий регрессии и динамики.
Регрессия, выражаемая уравнением параболы второго порядка. Нередко зависимость между переменными величинами Y и X выражается уравнением параболы второго порядка
. (25)
Отысканию параметров a, b и c уравнения (25) удовлетворяет следующая система нормальных уравнений:
;
;
.
Решением данной системы являются следующие уравнения:
;
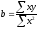и
,
где
– определитель системы;n
– число членов ряда регрессии; yi
– значения зависимой переменной Y;
– отклонения членов ряда независимой
переменнойX
от средней величины.
Регрессия, выражаемая уравнением параболы третьего порядка. Среди различных форм параболической зависимости между переменными величинами встречаются и такие, которые наилучшим образом описываются уравнением параболы третьего порядка:
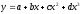. (26)
Для определения параметров уравнения (26) используют следующую систему нормальных уравнений:
;
;
;
.
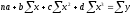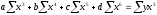Решение этой системы относительно параметров a, b, c и d приводит к следующим формулам:
;
;
;
,
где
и
– определители системы;n
– число членов ряда регрессии; xi
и yi
– значения переменных, из которых
независимая переменная выражается
отклонениями членов ряда от их средней
величины.
Регрессия, выражаемая уравнением гиперболы первого порядка. В зависимости от наклона кривой регрессии к осям прямоугольных координат корреляционная зависимость между переменными величинами может быть выражена тем или иным уравнением гиперболы.
В простейшем виде гиперболическая зависимость между переменными Y и X описывается уравнением гиперболы первого порядка:
.
(27)
Для определения параметров a и b уравнения (27) служит следующая система нормальных уравнений:
;
.
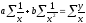Совместное решение этой системы относительно параметров a и b приводит к следующим формулам:
;
,
где
– определитель системы;x
– значения независимой переменной; y
– значения зависимой переменной
величины; n
– число членов ряда регрессии.
Регрессия, выражаемая уравнением гиперболы второго порядка. Для нахождения выравнивающих значений зависимой переменной иногда более подходящим оказывается уравнение гиперболы второго порядка
. (28)
Для определения параметров a и b уравнения (28) служит следующая система нормальных уравнений:
;
.
Решение этой системы относительно параметров a и b приводит к следующим формулам:
;
,
где
.
Регрессия, выражаемая уравнением гиперболы третьего порядка. В практике встречаются случаи, когда с увеличением независимой переменной X зависимая переменная Y, быстро убывая, вскоре стабилизируется на определенном уровне, принимая более или менее постоянные значения. В таких ситуациях для выравнивания эмпирического ряда регрессии можно использовать уравнение гиперболы третьего порядка:
. (29)
Для определения параметров a и b уравнения (29) служит следующая система нормальных уравнений:
;
.
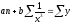Решая совместно эти уравнения относительно параметров a и b, получаем следующие формулы:
;
,
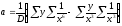где
.
Регрессия, выражаемая уравнением гиперболы первого порядка с тремя неизвестными: a, b и c. Если с увеличением независимой переменной X зависимая переменная Y быстро убывает, достигая некоторого предела, за которым обнаруживается более или менее стабильное течение функции, то для выравнивания эмпирических значений зависимой перменной может быть использовано уравнение гиперболы следующего вида:
. (30)
Для определения параметров a, b и с уравнения (30) служит следующая система нормальных уравнений:
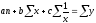
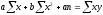
Регрессия, выражаемая уравнением показательного типа. В тех случаях, когда основная тенденция эмпирического ряда регрессии следует или оказывается близкой закону геометрической прогрессии, его удается описать уравнением экспоненциального, или показательного, типа:
или
. (31)
Использование уравнения такого вида связано с их логарифмированием, что позволяет трансформировать их в уравнение прямой линии. Так, в данной случае
(32)
Логарифмическое преобразование исходного уравнения регрессии (31) не только облегчает вычисление параметров a и b, но и служит своего рода контролем того, насколько правильно выбрано применяемое уравнение. В частности, условием правильного выбора уравнения показательного типа служит требование, чтобы точки x и lg y в системе прямоугольных координат находились на одной прямой.
Для определения параметров уравнения (32) служит следующая система нормальных уравнений:
;
.
Совместное решение этой системы приводит к следующим формулам:
;
где
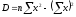;n
– число членов ряда; y
– значения членов ряда зависимой
переменной Y;
x
– значения членов ряда независимой
переменной X,
которые обычно выражаются, как и в
предыдущем случае, числами натурального
ряда.
Регрессия, выражаемая уравнением степенного типа. Зависимость между переменными величинами Y и X иногда хорошо описывается уравнением степенного типа
,
(33)
которое в результате логарифмирования превращается в уравнение прямой линии:
. (34)
Условием правильного применения уравнения (34) служит требование, чтобы точки lg y и lg x в системе прямоугольных координат находились на одной прямой.
Для определения параметров a и b уравнения степенного типа (34) служит следующая система нормальных уравнений:
;
.
Из решения этой системы получаются формулы
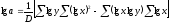и
,
где
– определитель системы;n
– число членов ряда регрессии; x
и y
– значения членов ряда независимой и
зависимой переменных величин.
Регрессия, выражаемая уравнением логистической кривой. Значительный интерес для эколога представляет логистическая зависимость между переменными величинами. Зависимость такого рода встречается во многих случаях, например при изменении состава популяции в замкнутой среде обитания, когда начальное число особей сначала быстро возрастает, затем темп роста популяции также быстро снижается и популяции переходят в состояние динамического равновесия. Графически эта закономерность изображается в виде S-образной кривой, которая описывается уравнением Ферхюльста:
,
(35)
где y – учитываемый признак; t – время, прошедшее от начальной, или базисной (с), величины признака, с которой начато его измерение, до предельной в данных условиях величины N, которой он достиг за время t; a и b – параметры уравнения, определяющие характер логистической кривой.
Путем логарифмического преобразования уравнение (35) приобретает следующее выражение:
.
Обозначим
черезz,
получаем уравнение линейной регрессии:
. (36)
Определению параметров a и b уравнения (36) удовлетворяет следующая система нормальных уравнений:
;
Решая совместно эти уравнения относительно параметров a и b, получаем следующие формулы:
;
,
где
.