Методическое пособие

по физике и астрономии для

учащихся 9 классов по подготовке к государственному тестированию.

Город Рудный, 2006 год.

Содержание.

1. Основы кинематики ­­­­­­­­­­­­­­­­­­­­­­­­3

2. Основы динамики 8

3. Законы сохранения в механики 13

4. Колебания и волны 15

5. Механика жидкостей и газов 19

6. Основные положения МКТ 21

7. Основы термодинамики 22

8. Электрическое поле. Основные понятия и законы 28

9. Постоянный ток 31

10. Магнитное поле 35

11. Оптика 38

12. Строение атома. Атомные явления 44

13. Астрономия 49

Составители: Балыкова О.В., Бер А.В., Бойко Т.В., Бондарева Т.А., Герасимов Г.М., Гнедышева Л.М., Ибрашева З.С., Козлова З.Л., Коновалова О.В., Костомарова Е.В., Лой Т.А., Нехайчик Л.Н., Попова Л.В., Таранухина Л.Д., Циттель Е.А., Шаинов Б.Д.

Редакторы: Герасимов Г.М., Никулина Н.М., Циттель Е.А.

Техническое обеспечение: Ищенко И.А., Циттель И.

Основы кинематики.

Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени.

Тело, размерами которого в дан­ных условиях движения можно пренебречь, называют материальной точкой.

Система координат, тело отсчета, с которым она связана, и прибор для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела.

Направленный отрезок прямой соединяющей начальное и конечное положение тела называют перемещением.

Траектория – линия, вдоль которой движется тело (прямая линия, окружность, парабола и другие).

Пройденный путь – длина траектории.

Векторы и действия над ними

Сложение векторов:

Правило треугольника

Правило параллелограмма

Вычитание векторов:

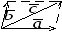
Если векторы действуют вдоль одной прямой, или параллельно друг другу, то они могут быть направлены в одну сторону или в противоположные стороны. По мо­дулю результирующий вектор равен арифметической сумме либо арифметической разности модулей складываемых векторов. Результирую­щий вектор направлен в сторону боль­шего по модулю вектора.

Проекции вектора на координатные оси. Действия над проекциями.

Длину отрезка между проек­циями начала и конца вектора, взятую со знаком «+» или «-», называют проекцией вектора на ось. Проекция вектора - величина скалярная. Если вектор перпендикулярен оси, то при любом направлении вектора его проекция на ось равна нулю. Если вектор параллелен

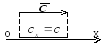
оси, то модуль его проекции равен модулю самого вектора. При этом если вектор и ось сонаправлены, то проекция положительна, если направления вектора и оси противоположны друг другу, проекция вектора отрицательна.

Проекция суммы векторов на коорди­натную ось равна алгебраической сумме проекций складываемых век­торов на ту же ось.

Прямолинейное равномерное движение

Равномерное движение – движение, при котором тело за равные промежутки времени совершает равные перемещения.

Скорость () – физическая величина, которая определяет перемещение (s) тела за единицу времени (t) (скорость 10 м/с показывает, что тело за 1 секунду перемещается на 10 метров). Формула скорости

Уравнение координаты при равномерном движении: , гдеx₀–начальная координата (м),– проекция скорости (м/с),t–время (с).

Прямолинейное неравномерное движение

Неравномерное движение, при котором скорость тела за каждую единицу времени или за любые равные промежутки времени из­меняется одинаково, называют равноускоренным.

Средняя скорость: – при неравномерном движении.

Мгновенной скоростью тела называется скорость тела в данный момент времени или в данной точке траектории. Мгновенная скорость, или ско­рость в данной точке, равна отно­шению достаточно малого переме­щения на участке траектории, при­мыкающем к этой точке, к малому промежутку времени, в течение кото­рого это перемещение совершается.

Ускорением тела при его равно­ускоренном движении называется величина, равная отношению изме­нения скорости к промежутку вре­мени, в течение которого это из­менение произошло. .

В

a>0

системе СИ ускорение выражается в мет­рах в секунду за секунду или в метрах на секунду в квадрате (м/с²).

Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно раз­гоняется a>0) или быстро теряет ее (при торможении a<0).

Уравнение зависимости скорости от времени.

Перемещение при прямолинейном равноускоренном движении равно площади фигуры, ограниченной осями и графиком. Перемещение находится по формулам.Уравнение координаты при равноускоренном движении .

Свободное падение тел. Ускорение свободного падения

Ускорение свободно­го падения: =9,81 м/с² , вектор всегда направлен вниз. Вверх брошенное тело движется с убы­вающей скоростью.

Общая формула	Свободное падение	Движение тела брошенного вверх

Криволинейное движение.

Криволинейное движение — дви­жение по дугам окружностей с ускорением, даже если по модулю скорость постоянна. Ускорение связано с изменением направления скорости.

Ускорение (a) тела, равномерно дви­жущегося по окружности в любой ее точке, центростремительное, т. е. направлено по радиусу (r) окружности к ее центру.) В любой точке вектор ускорения перпендикулярен вектору линейной скорости (). .

Линейная и угловая скорости.

Радиус, прове­денный из центра окружности к мате­риальной точке, за время (t) описал угол φ (фи), который называют угловым перемещением. Угловое перемещение в Между­народной системе единиц выражают в радианах. Радиан — центральный угол между двумя радиуса­ми окружности, длина дуги между которыми равна радиусу. Его сокращенное обозначение— 1 рад.

Угловую скорость принято обозна­чать буквой ω (омега): , где

Частотой (ню) обращения называют число оборотов мате­риальной точки вокруг центра обращения за секунду:, где N — число оборотов, совершенных за времяt.

Периодом (Т) обращения называют время, в течение ко­торого совершается один оборот точки по окружности. ,

Связь между периодом и частотой устанавливаем на примере. Пусть 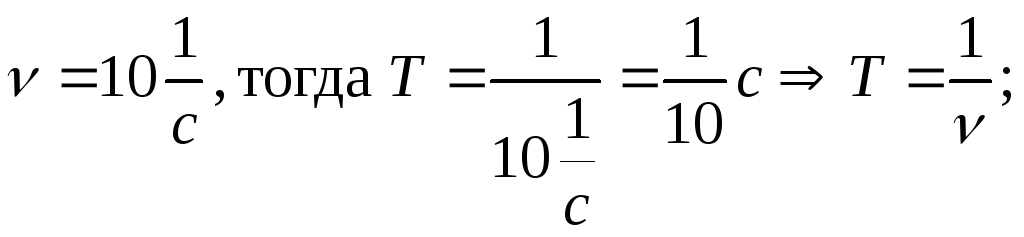частота равна.

Угловое перемещение φ тела за период Т равно 2. Поэтому угловая скорость, или. ЗаТ точка проходит путь Линейная скорость тела, движущегося по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории:или.Связь линейной скорости и угловой находится по следующим формулам: