16. Предел функции. Непрерывность функции многих переменных.

см. все в предыдущем билете

Теорема: Свойства непрерывных функций многих переменных на замкнутых множествах.

Пусть — замкнутое множество (подразумевается любое пространство). Тогда:

1) ограничена на , т.е. существует m больше нуля, такое, что М принадлежащей следует:

2) существуют числа M, m , такие, что следует:

3)

17. Частные приращения и частные производные. Дифференцируемость ф.М.П. Полный дифференциал, его связь с частными производными. Геометрический смысл полного дифференциала.

о пр.: Приращением функции в точке М0 с координатами называется выражение

опр.: частным приращением функции 2-х переменных Z=f(x,y) по Х в точке М называется выражение , частным приращением по у соответственно

опр.: Частной производной функции по х называется , если он существует. Частной производной функции по у называется , если этот предел существует.

Г еометрический смысл: Частная производная равна тангенсу угла наклона касательной, проведенной к функции с плоскостью

18. Частные производные и частные дифференциалы высших порядков. Формула Тейлора.

19. Дифференцирование сложной функции от двух переменных.

20. Неявные функции. Теорема существования. Дифференцирование неявных функций.

21. Экстремумы ФМП. Необходимое условие экстремума Ф.М.П.

22. Э. Ф.М.П. Достаточные условия экстремума функции. 2-х переменных.

23. Квадратичные формы N-ного порядка. Матрица квадратичной формы. Критерий Сильвестра.

24. Э.Ф.М.П.: Достаточные условия экстремума функций м.п.

25. Постановка задачи об условном экстремуме.

Основная постановка задачи: Найти экстремумы данной функции , где

26. Функция Лагранжа. Множители Лагранжа. Теорема о необходимых и остаточных условиях условного экстремума.

27. Первообразная и неопределенный интеграл. Св-ва неопределенного интеграла.

Опр. 1: Первообразной для данной функции , определенной на интервале I называется функция такая, что .

Теорема: Все первообразные , ... для функции на интервале I отличаются на С, т.е. = + С.

Доказательство по теор. Лагранжа: , тогда .

Теор. 2: Множество первообразных называется неопределенным интегралом.

Свойства неопределенного интеграла:

1. 2. 3.

28. Таблица первообразных

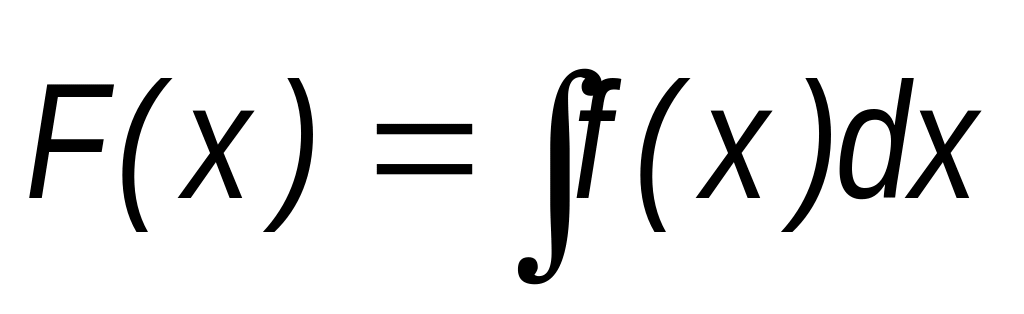
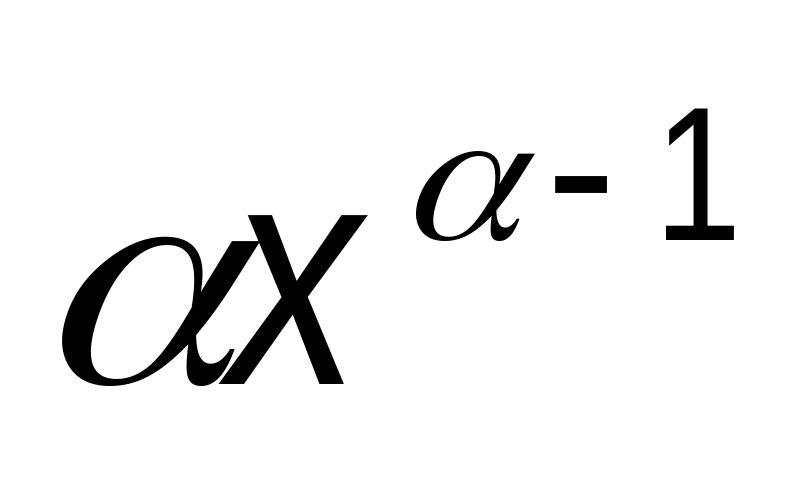
			+ C
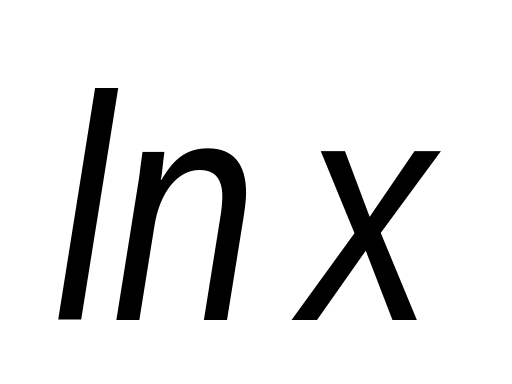	1/x	1/x	+C
℮x	℮x	℮x	℮x + C
sin x	cos x	cos x	sin x + C
cos x	-sin x	sin x	-cos x
tg x			tg x + C
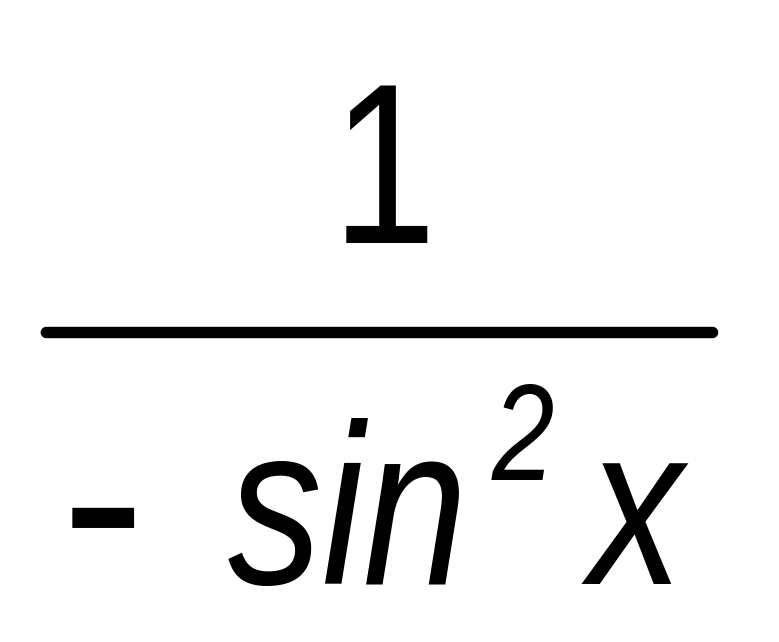
ctg x			-ctg x + C
arctg x			arctg x + C
arcsin x			arcsin x + C - arccos x + C