§ 5. Обобщающие примеры по теме: «Алгебра матриц»
Набор обобщающих Примеров соответствует требованиям «Семестрового плана» при изучении темы: «Алгебра матриц». Эти Примеры предназначены закрепить навыки применения общих алгоритмов решений, установленных в поясняющих Примерах.
☺ ☻ ☺
Пример
1–788:Вычислить
произведение матриц: C=AB=
.
Решение:
В таблице представлена схема вычисления произведения матриц AиB:
▫ для вычисления столбца-1 матрицы Cнад матрицей размещаем столбец-1 матрицыB;
▫ для вычисления столбца-2 матрицы Cнад матрицей размещаем столбец-2 матрицыB;
-
Столбец
3
2
Столбец
Столбец
4
5
Столбец
3
-2
5
3
-2
2
5
-4
7
5
-4
0
Использование
технологического шаблона в виде таблицы
позволит отработать алгоритм вычисления
произведения матриц и защитить от ошибок
в вычислениях. Проследим вычисление
столбца-1 матрицы C:
=
,
=
.
Ответ: C=
.
Пример 2–790:
Вычислить
произведение матриц: C=AB=
.
Решение:
В таблице представлена схема вычисления произведения матриц AиB:
▫ для вычисления столбца-1 матрицы Cнад матрицей размещаем столбец-1 матрицыB;
▫ для вычисления столбца-2 матрицы Cнад матрицей размещаем столбец-2 матрицыB;
▫ для вычисления столбца-3 матрицы Cнад матрицей размещаем столбец-3 матрицыB;
|
Столбец |
2 |
1 |
1 |
Столбец |
Столбец |
5 |
2 |
3 |
Столбец |
Столбец |
6 |
5 |
2 |
Столбец |
|
|
1 |
-3 |
2 |
1 |
|
1 |
-3 |
2 |
5 |
|
1 |
-3 |
2 |
-5 |
|
|
3 |
-4 |
1 |
3 |
|
3 |
-4 |
1 |
10 |
|
3 |
-4 |
1 |
0 |
|
|
2 |
-5 |
3 |
2 |
|
2 |
-5 |
3 |
9 |
|
2 |
-5 |
3 |
-7 |
Из таблицы видим ответ. Проследим вычисление столбца-1 матрицы C:
=
,
=
,
=
.
Ответ:
=
.
Пример
3–792:Вычислить
произведение матриц: C=AB=
.
Решение:
В таблице представлена схема вычисления произведения матриц AиB:
▫ для вычисления столбца-1 матрицы Cнад матрицей размещаем столбец-1 матрицыB;
▫ для вычисления столбца-2 матрицы Cнад матрицей размещаем столбец-2 матрицыB;
▫ для вычисления столбца-3 матрицы Cнад матрицей размещаем столбец-3 матрицыB;
▫ для вычисления столбца-4 матрицы Cнад матрицей размещаем столбец-4 матрицыB.
-
Столбец
7
5
3
2
Столбец
Столбец
8
7
4
1
Столбец
2
-1
3
-4
10
2
-1
3
-4
17
3
-2
4
-3
17
3
-2
4
-3
23
5
-3
-2
1
16
5
-3
-2
1
12
3
-3
-1
2
7
3
-3
-1
2
1
(продолжение таблицы).
-
Столбец
6
4
5
1
Столбец
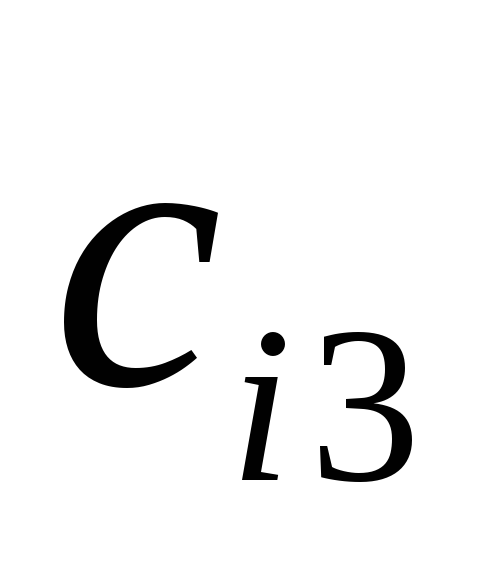
Столбец
9
5
6
2
Столбец
2
-1
3
-4
19
2
-1
3
-4
23
3
-2
4
-3
27
3
-2
4
-3
35
5
-3
-2
1
9
5
-3
-2
1
20
3
-3
-1
2
3
3
-3
-1
2
10
Из таблицы видим ответ. Проследим вычисление столбца-1 матрицы C:
=
,
=
,
=
,
=
.
Ответ: C=
.
Пример
4–796:Вычислить
произведение матриц: C=ABD=
.
Решение:
В таблице представлена схема вычисления произведения матриц AB=T.
-
Столбец
-28
38
Столбец
Столбец
93
-126
Столбец
4
3
2
4
3
-6
7
5
-6
7
5
21
В таблице представлена схема вычисления произведения матриц C= T D.
-
Столбец
7
2
Столбец
Столбец
3
1
Столбец
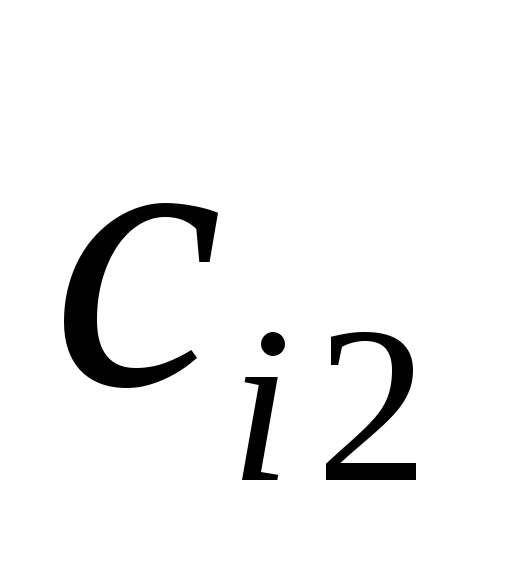
2
-6
2
2
-6
0
-6
21
0
-6
21
3
Ответ: C=
.
Пример
5–799:Вычислить: C=A3,
еслиA
=
.
Решение:
1)
Применим вычислительную схему:
C=
A3
=
AAA
=
=
TA.
В таблице представлена схема вычисления произведения матриц AA=T.
-
Столбец
1
3
Столбец
Столбец
-2
-4
Столбец
1
-2
-5
1
-2
6
3
-4
-9
3
-4
10
В таблице представлена схема вычисления произведения матриц C= TA.
-
Столбец
1
3
Столбец
Столбец
-2
-4
Столбец
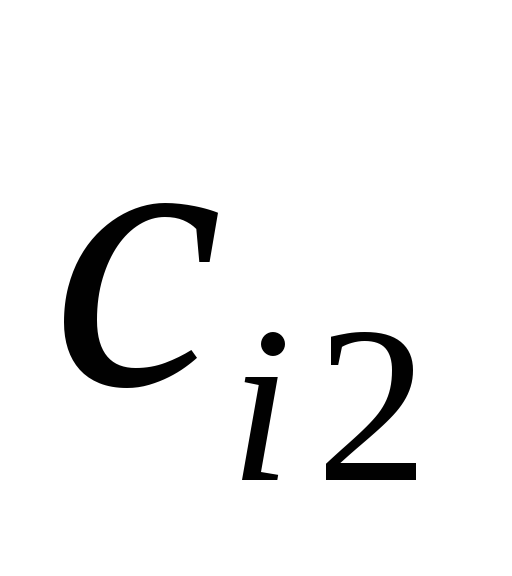
-5
6
13
-5
6
-14
-9
10
21
-9
10
-22
Ответ: C=
.
Пример
6–801:
Вычислить: C=An,
еслиA
=
,
или C=
AAA…
Решение:
В таблице представлена схема вычисления произведения матриц AA=B=A2.
-
Столбец
2
3
Столбец
Столбец
-1
-2
Столбец
2
-1
1
2
-1
0
3
-2
0
3
-2
1
В таблице представлена схема вычисления произведения матриц D= BA=A3.
-
Столбец
2
3
Столбец
Столбец
-1
-2
Столбец
1
0
2
1
0
-1
0
1
3
0
1
-2
Сравним полученные результаты умножений: A=A1 =A3; в то же времяA4 = A3A. Используя результат:A3 =A, получаем равенствоA4 = A2.
Закономерность
очевидна: если
=
– чётное, тоC=An=
,если
=
– нечётное, тоC=An=
.
Ответ: если
=
– чётное, тоC=An=
,если
=
– нечётное, тоC=An=
.
Пример
7–805:
Вычислить: C
=An,
еслиA
=
,
или C=
AAA…
Решение:
В таблице представлена схема вычисления произведения матриц AA=T.
-
Столбец
λ
0
Столбец
Столбец
1
λ
Столбец
λ
1
λ2
λ
1
2 λ
0
λ
0
0
λ
λ2
В таблице представлена схема вычисления произведения матриц C= TA.
-
Столбец
λ
0
Столбец
Столбец
1
λ
Столбец
λ2
2 λ
λ3
λ2
2 λ
3λ2
0
λ2
0
0
λ2
λ3
Анализируя
полученные результаты, замечаем
закономерность: C=
=
.Для её доказательстваприменим
метод математической индукции: будем
считать, что утверждение C– верно. Тогда
вычислим выражение D=
=
·
:
В таблице представлена схема вычисления произведения матриц D= CA. с учётом принятого допущения о верности C.
-
Столбец
λ
0
Столбец
Столбец
1
λ
Столбец
λn
n·λn-1
λn+1
λn
n·λn-1
(n+1)·λn
0
λn
0
0
λn
λn
Видим, что
утверждение: D=
=
верно → значит полученная формула:
=
- верна!
Ответ: C=
.
Пример 8–810: Доказать, что если для матрицAиBоба произведенияAB=C1иBA=C2существуют, причемAB=BA, то матрицыAиBквадратные и имеют одинаковый порядок.
Решение:
Замечание: предполагается, что умножение матриц определено по правилу строка – столбец: количество столбцов в матрице A равно количеству строк в матрице B.
1). Так как возможно составить произведение AB, то число строк матрицыBдолжно быть равным числу столбцов матрицыA, это отражено на схеме:
|
|
n |
|
|
|
k |
|
|
|
k | ||||||||||||
|
m |
A |
|
|
n |
B |
|
|
m |
C1 | ||||||||||||
|
|
|
|
| ||||||||||||||||||
|
|
• |
|
═ | ||||||||||||||||||
|
|
| ||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||
|
|
|
|
| ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
2). Так как возможно составить произведение BA, то число строк матрицыAдолжно быть равным числу столбцов матрицыB, это отражено на схеме:
|
|
k |
|
|
|
n |
|
|
|
n | |||||||
|
n |
B |
|
|
m |
A |
|
|
n |
C2 | |||||||
|
|
|
|
| |||||||||||||
|
|
• |
|
═ | |||||||||||||
|
|
| |||||||||||||||
|
|
|
|
| |||||||||||||
|
|
|
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
3). Из представленных схем следует: необходимо k=m.
4). Из условия:
следует→n= m. Имеем
окончательно: матрицыAиBквадратные и имеют
одинаковый порядок:
.
Ответ: доказано.
Пример
9–816:
Доказать, что если матрицыAиB– квадратные одного
порядка, причём
=
,
то всегда справедливо утверждение:
.
Решение:
1) Вспомним
формулу бинома Ньютона: 
,
где a
и b
числа.
При получении формулы бинома Ньютона
были использованы свойства
элементов
a,b:
переместительное, сочетательное и
распределительное в операции умножения.
2) В общем
случае для любых двух матриц A
и B
операция умножения матриц обладает
свойствами: сочетательное и
распределительное. Дополнительное
условие для заданных матриц A
и B:
выполнение равенства
=
добавляет операции умножения свойство
переместительное для элементов:
A
и
B.
3) Сравнивая свойства элементов a и b со свойствами элементов A и B, находим их одинаковыми для совокупности операций, используемых в формуле бинома Ньютона → заданное утверждение справедливо!
Ответ: доказано.
Пример
10–822:
Найти все матрицы, перестановочные с
матрицей:
=
.
Решение:
1) Пусть
имеем матрицу: 
,
такую, что
=
.
Учитывая правило умножения матриц,
легко заметить, что умножение этих
матриц возможно только в случае, если
матрица 
-
квадратная, причём той же размерности,
что матрица 
.
2) Примем:
=
,
и запишем выражение 
=
:
В таблице представлена схема вычисления произведения матриц T =AB.
-
Столбец
a
b
Столбец
Столбец
c
d
Столбец
1
2
a+2b
1
2
c+2d
3
4
3a+4b
3
4
3c+4d
3)
Примем: 
=
,
и запишем выражение 
=
:
В таблице представлена схема вычисления произведения матриц C=BA.
-
Столбец
1
3
Столбец
Столбец
2
4
Столбец
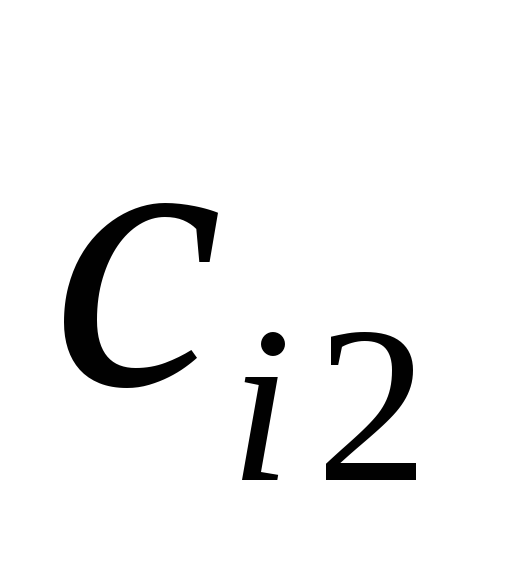
a
c
a+3c
a
c
2a+4c
b
d
b+3d
b
d
2b+4d
4)
Воспользуемся равенством: 
→
получаем уравнения для вычисления
матрицы 
:
a+2b=a+3c → 2b=3c; 3a+4b= b+3d → a+b=d;
c+2d=2a+4c → 2d=2a+3c; 3c+4d=2b+4d → 3c=2b.
5) Используя полученные уравнения, примем: a → a; b → 3b; c → 2b; d → 3b+a. Используя принятые соотношения, получаем все перестановочные с заданной матрицей матрицы:
=
,
где a;
b
– любые числа.
Ответ:
=
,
гдеa;b– любые числа.
Пример 11–826: Найти все числаk, умножение на которые невырожденной матрицыAне изменяет ее определителя.
Решение:
Замечание: а) известно, что матрица A называется невырожденной, если её определитель не равен нулю: |A| ≠ 0; поэтому значение числа k существенно;
б) в
соответствии с правилом умножения
матрицы на число запишем: 
=
k·
.
1). Имеем: |kA|=
·|A|.
2). По условию:
|kA|=
·|A|=|A|.
Следует:
=1
→k=
,
причем считаем 1 – комплексное число.
Известно:
=
+
,k= 0,1, 2, … , (n–1).
Ответ:
=
+
,k= 0, 1, 2, … , (n–1).
Пример
12–828:Найти
значение многочлена: 
=
от матрицы: A=
.
Решение:
1) Вычислим матрицу
B=
,
используя схему вычислений, представленную
таблицей:
|
Столбец |
5 |
1 |
2 |
Столбец |
Столбец |
2 |
3 |
2 |
Столбец |
Столбец |
-3 |
-1 |
-1 |
Столбец |
|
|
5 |
2 |
-3 |
21 |
|
5 |
2 |
-3 |
10 |
|
5 |
2 |
-3 |
-14 |
|
|
1 |
3 |
-1 |
6 |
|
1 |
3 |
-1 |
9 |
|
1 |
3 |
-1 |
-5 |
|
|
2 |
2 |
-1 |
10 |
|
2 |
2 |
-1 |
8 |
|
2 |
2 |
-1 |
-7 |
2) Вычислим матрицу
C=
,
используя схему вычислений, представленную
таблицей:
|
Столбец |
5 |
1 |
2 |
Столбец |
Столбец |
2 |
3 |
2 |
Столбец |
Столбец |
-3 |
-1 |
-1 |
Столбец |
|
|
21 |
10 |
-14 |
87 |
|
21 |
10 |
-14 |
44 |
|
21 |
10 |
-14 |
-59 |
|
|
6 |
9 |
-5 |
29 |
|
6 |
9 |
-5 |
29 |
|
6 |
9 |
-5 |
-22 |
|
|
10 |
8 |
-7 |
44 |
|
10 |
8 |
-7 |
30 |
|
10 |
8 |
-7 |
-31 |
2) Запишем значение
многочлена: 
=
от матрицы: A:
=
–7
+13
–
=
.
Ответ:
=
=
.
☻
Вопросы для самопроверки:
Можно ли сложить матрицу с размерами (2х3) с матрицей с размерами (3х2)?
Можно ли умножить матрицу с размерами (2х3) на матрицу с размерами (2х3)?
Можно ли из одной матрицы вычесть другую? Каким условиям должны удовлетворять при этом матрицы? Какие размеры имеет матрица, являющаяся результатом этой операции?
Можно ли умножить матрицу A на матрицу A, если
?Назовите свойства операции сложения матриц. Попробуйте их доказать.
Назовите свойства операции умножения матрицы на число. Попробуйте их доказать.
Назовите свойства операции умножения матриц. Попробуйте их доказать. Почему операция перемножения матриц не коммутативна?
< * * * * * >