§ 3. Обобщающие примеры по теме: «Определители n-го порядка»

Набор обобщающих Примеров соответствует требованиям «Семестрового плана» при изучении темы: «Определители n-го порядков». Эти Примеры предназначены закрепить навыки применения общих алгоритмов решений, установленных в поясняющих Примерах.

☺ ☻ ☺

Пример 1–151:Определить четность подстановки: двумя способами: 1): подсчетом числа инверсий элементов ее нижней строки; 2) разложением подстановки в циклы и вычислением числа декремент.

Решение:

Способ 1. Определим четность подстановки подсчетом числа инверсий элементов ее нижней строки. Для подсчета числа инверсий воспользуемся таблицей, в которой указаны инверсии (символ: ♦) выделяемых элементов (символ: ☻) с последующими элементами (учет нарушений порядка):

4	1	5	2	3
☻	♦		♦	♦	=3
	☻				=0
		☻	♦	♦	=2
			☻		=0
————————————
Число инверсий :					=5

откуда следует: подстановка нечетная.

Способ 2. Воспользуемся определением декремента: d = n–s , где n – число элементов в подстановке, s = (число независимых циклов) + (число символов, оставшихся на месте). Четность декремента совпадает с четностью подстановки! Вычислим декремент:

а) разложим подстановку в произведение циклов: =(142)(35);

б) вычислим декремент: d = 5–2 = 3, откуда следует: подстановка нечетная.

Ответ:подстановка четная.

Пример 2–153:Определить четность подстановки: p=разложением подстановки в циклы и вычислением числа декремент.

Решение:

1) Разложим подстановку в произведение циклов: p=(182)(3)(467)(5).

2) Вычислим декремент: d = 8–4 =4, откуда следует: подстановка четная.

Ответ:p=(182)(3)(467)(5); подстановка четная.

Пример 3–165: Имеется запись подстановки в циклах:p = (7531)(246)(8)(9), найти запись этой подстановки в выражении с двумя перестановками.

Решение:

Используя правила построения циклов подстановки:

1) Запишем верхнюю строку подстановки: (1 2 3 4 5 6 7 8 9).

2) Отразим в нижней строке подстановки каждый из циклов:

▫ цикл: (7531) → (7→5→3→1→7) → (7 ● 1 ●3 ● 5 ● ●);

▫ цикл: (246) → (2→4→6→2) → (7 4 1 6 3 2 5 ● ●);

▫ цикл: (8) → (8→8) → (7 4 1 6 3 2 5 8 ●);

▫ цикл: (9) → (9→9) → (7 4 1 6 3 2 5 8 9).

3) Подстановка принимает вид: .

Ответ: .

Пример 4–189: Входит ли произведение:в определитель? Если входит, то с каким знаком?

Решение:

1) Составим для заданного члена определителя подстановку: .

2) Разложим подстановку в произведение циклов: p=(1236)(45).

3) Вычислим декремент: d = 6–2 = 4 – чётное число → подстановка четная → произведение входит в определитель со знаком .

Ответ:входит со знаком .

Пример 5–191: Входит ли произведение:в определитель? Если входит, то с каким знаком?

Решение:

1) Составим для заданного члена определителя подстановку: .

2) Разложим подстановку в произведение циклов: p=(16)(27)(3)(4)(5).

3) Вычислим декремент: d = 7–5 = 2 – чётное число → подстановка четная → произведение входит в определитель со знаком .

Ответ:входит со знаком .

Пример 6–199: Найти члены определителя 4-го порядка, содержащие элементи входящие в определитель со знаком плюс.

Решение:

1) Запишем все члены определителя, содержащие заданный элемент: ··,

или: ·(–1)·(++–––).

2) Со знаком в определитель входят: , , .

Ответ:,,.

Пример 7–200:Найти члены определителя, содержащие x⁴иx³: .

Решение:

1) Найти член определителя, содержащий x⁴, достаточно просто: должны участвовать элементы главной диагонали → имеем член: 10x⁴.

2) Ответить на поставленный вопрос: выделение членов с x⁴ и x³ можно, воспользовавшись разложением определителя по 1-му столбцу:

d = 5x+ x+ 1+ x=

= 10x⁴+ … – x(1·x·2x)+ … – x(3·x·x) + … = 10x⁴ – 5 x³ + …

Замечание: в разложении многоточия отражают члены разложения, имеющие величину в степенях, меньших 4-й и 3-й.

Ответ: 10x⁴; – 5 x³.

Пример 8–201: С каким знаком входит в определитель порядкаnпроизведение элементов главной диагонали?

Решение:

1) Произведение элементов главной диагонали: .

2) Выделенным элементам соответствует подстановка: p= – чётная подстановка, так как число инверсий в этой подстановке равно 0 → произведение входит в определитель со знаком .

Ответ:входит со знаком .

Пример 9–203: Вычислить:d=,пользуясь только его определением.

Замечание: имеется в виду: записываем суммучленов определителясо знаками, определяемыми подстановками (не используя разложения по строке!).

Решение:

1) Член определителя формируется из его элементов по правилу: берём по одному из каждой строки и каждого столбца.

2) Так как из первой строки в каждый член определителя входит один элемент обязательно, то ненулевой член получаем только от участия элемента . Как только элемент включён в член определителя, столбец-1 более не может использоваться! Теперь для получения ненулевого члена определителя из строки-2 подойдёт только элемент , и исключается дальнейшее участие столбца-2...

3) Продолжая формирование членов определителя, дойдём до последнего элемента, расположенного на главной диагонали : получаем единственный член определителя, не равный нулю: , его знак определяется подстановкой: p= – чётная подстановка, так как число инверсий в этой подстановке равно 0 → произведение входит в определитель со знаком . Значит: d=

Ответ:.

Пример 10–205:Вычислить определитель: d=, пользуясь только определением определителя.

Решение:

Способ 1. Из определения: каждый член определителя содержит элементы из разных строк и разных столбцов». Выберем произвольный член минора

а) каждый член определителя должен состоять из 5-ти сомножителей;

б) если выбрали элементы из двух первых строк и первых столбцов для использования в записи члена определителя, то 5-й может быть только нулем. Это минимальное количество нулей в выражении члена определителя: их может быть и два, и три!

в) следует: d = 0.

Способ 2. Можно было бы воспользоваться теоремой Лапласа: использование разложения оп­ределителя по k строкам или k столбцам... Это значит: если выделим минор М 2-го порядка из строк 1,2, (не равен нулю!), то минор M′ в любом случае будет содержать столбец, сплошь со­стоящий из нулей. Значит d = 0.

Ответ: доказательство в тексте.

Пример 11–208: Решить уравнение: d==0.

Решение:

Используя свойства определителя, выполним действия:

1) вычтем 1-ю строку из 2-й, 3-й, и так далее строк → получаем определитель треугольного вида (ниже главной диагонали все элементы нули, остальные произвольные);

2) известно (легко доказывается!), что определитель треугольного вида равен произведе­нию его диагональных элементов: d = 1·(–x)(1–x)(2–x)…(n–1–x) .

Тогда решение уравнения очевидно: x= 0, x= 1, x= 2, … x= n–1.

Ответ:x=0, 1, 2, … , (n–1).

Пример 12–210: Найти элемент определителяn-го порядка, симметричный элементуотносительноцентраопределителя.

Решение:

1) Геометрически определитель можно представить в виде квадрата. Это значит, что по вертикали координата строки элемента относительно нижней стороны квадрата равна . Аналогично, по горизонтали координата строки элемента относительно правой стороны квадрата равна .

2) Так как осуществляется преобразование симметрии относительно центра квадрата, то симметричный элемент должен занять строку с номером: и столбец с номером: .

3) Получена формула симметричного преобразования относительно центра определителя:

→

Ответ:.

Пример 13–213: Как изменится определитель порядкаn, если его строки записать в обратном порядке?

Решение:

Замечание: предложение записать строки в обратном порядке равносильно (по свойству опре­делителя!) предложению переставить столбцы определителя (обозначены: a_i) так, что:

a1

a2

a3

. . .

an-1

an

Транспозиций

. . .

n–1

an

a1

a2

. . .

an-2

an-1

. . .

n–2

an

an-1

a1

. . .

an-3

an-2

. . .

n–3

. . . . . . . . . . . . . .

an

an-1

an-2

an-3

. . .

a1

a2

1

an

an-1

an-2

an-3

. . .

a2

a1

Для того, чтобы расположить столбцы в обратном порядке, необходимо совершить (см. принятую схему!) транспозиций: N = (n–1) + (n–2) + … + 1 = {арифметическая прогрессия, в ко­торой 1-й член равен (n-1), а последний 1} = n(n–1).

Известно, что каждая транспозиция меняет знак определителя. Это значит, что после вы­полнения всех перестановок мы получим определитель: d·.

Ответ: получим определитель:.

Пример 14–215: Как изменится определитель порядкаn, если каждый его элемент заменить элементом, симметричным с данным элементом относительно побочной диагонали?

Решение:

Замечания: 1) при любом n, как показано в Примере 13–213, симметрию относительно побочной диагонали можно заменить тремя преобразованиями: 1) симметрия относительно горизонтальной средней линии определителя; 2) симметрия относительно вертикальной средней линии определителя; 3) транспонирование относительно главной диагонали определителя;

2) реализацию схемы преобразований удобно проследить на примере определителя 5-го порядка:

│

⁄

♥

♥

\

♦

⁄

♥

\

⁄

─

─

\

⁄

♦

♦

\

⁄

♥

♦

\

│

1) Независимо от n (n = 2k+1 – нечетное, или n = 2k – четное), симметрия относительно горизонтальной и вертикальной средних линий определителя может быть осуществлена при помощи 2·k транспозиций. Так как 2·k – четное число → определитель не изменяется.

2) Так как транспонирование определителя относительно главной диагонали определителя не ме­няет, то в результате заданного в задаче преобразования определитель не меняется.

Ответ:определитель не меняется.

Пример 15–216: Определитель называется кососимметрическим, если элементы, симметрично лежа­щие относительно главной диагонали, отличаются знаком:для любых, а элементы главной диагонали равны нулю:. Доказать, что кососимметриче­ский определитель нечетного порядкаравен нулю.

Решение:

Выполним преобразования:

1) Пусть в определителе видим у каждого элемента над главной диагональю знак минус: если на самом деле , его можно записать его в виде –(–).

2) Транспонируем определитель (определитель не меняется) → теперь все минусы пере­местились под главную диагональ;

3) Вынесем (–1) из каждой строки полученного определителя (определитель не меняется), перед определителем появился множитель , а сам определитель возвратился к ис­ходному виду. Это значит: d =·d=·d=–d. Отсюда следует: d = 0.

Ответ: доказано.

Пример 16–236: Разлагая определитель по 3-й строке, вычислить: .

Решение:

1) Запишем: d=a+b+c+e,

или: d=–+–.

2) Вычислим все определители разложения:

=(1)= = (2) == (3) ==8;

Операции: (1): [C1]+[C2]; [C2]–[C3]. (2): [C2]–[C1]; [C3]–[C1]·2. (3): применяем разложение определителя по строке-2 и завершаем вычисление.

=(1)= = (2) =–3·=–15;

Операции: (1): [C1]–[C3]·2. (2): применяем разложение определителя по столбцу-2 и завершаем вычисление.

=(1)= = (2) =–3·=12;

Операции: (1): [C1]–[C3]·2. (2): применяем разложение определителя по столбцу-2 и завершаем вычисление.

=(1)= = (2) == (3) ==19.

Операции: (1): [C2]+[C3]; [C3]–[C1]. (2): [R2]–[R1]; [R3]–[R1]·3. (3): применяем разложение определителя по столбцу-2 и завершаем вычисление.

3) Окончательно имеем: = .

Ответ: d=.

Пример 17–238: Вычислить определитель: .

Решение:

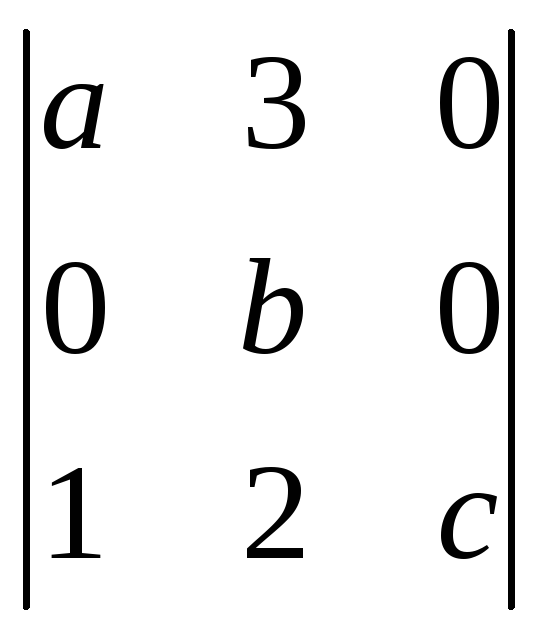Вычисляем определитель: =(1)=·= (2) =·=.

Операции: (1): применим разложение определителя по строке-4. (2): применяем разложение по столбцу-3 и завершаем вычисление.

Ответ:.

Пример 18–271: Вычислить определитель: .

Решение:

1) Запишем: d=(1)==(2)==(3)==(4)=

==(5)==5.

Операции: (1): [C2]–[C3]; [C2]–[C3] ; [C4]–[C1] ; [C3]–[C4]. (2): [R1]–[R5]. (3): применяем разложение определителя по строке-1. (4): [R1]–[R4]. (5): применяем разложение определителя по строке-1; [R1]–[R3] и завершаем вычисление.

Ответ: d=5.

Пример 19–279: Вычислить определитель: d=.

Решение:

Используя свойства определителя, выполним действия:

1) Прибавим 1-ю строку к 2-й, 3-й, и т.д. строкам → получен определитель треугольного вида с элементами на главной диагонали 1, 2, 3, …, n;

2) Известно, что такой определитель равен произведению элементов расположенных на главной диагонали: 1·2·3· … · n = n!

Ответ: d= n!

☻

Вопросы для самопроверки:

1. Перестановка – это матрица?

2. Что такое «транспозиция» двух элементов перестановки?

3. Что такое «инверсия» для двух выделенных элементов перестановки?

4. Что такое «порядок» для двух выделенных элементов перестановки?

5. Чему равна сумма чисел инверсий и порядка в любой перестановке чисел 1, 2, … , 99.

6. Подстановка – это матрица?

7. Что такое «транспозиция» столбцов подстановки?

8. Что такое «инверсия» в подстановке?

9. Что такое «порядок» в подстановке?

10. Чему равна сумма числа инверсий и числа порядков в любой подстановке чисел 1, 2, … , 99.

11. Может ли определитель n-го порядка не быть числом?

12. Изменится ли определитель n-го порядка, если в нем строки заменить столбцами и наоборот?

13. Изменится ли определитель n-го порядка, если в нем строки (или столбцы) поменять местами?

14. Изменится ли определитель n-го порядка, если в нем из одной строки вычесть другую строку?

15. Изменится ли определитель n-го порядка, если в нем из одного столбца вычесть другой столбец?

16. Изменится ли определитель n-го порядка, если в нем строку умножить на число 2?

17. Применение теоремы Лапласа предполагает уменьшение трудоемкости вычисления определителей высокого по­рядка?

18. Может ли произведение нескольких невырожденных квадратных матриц n-го порядка дать в результате вырож­денную матрицу?

< * * * * * >