65

ЛА: Глава 3

Глава 3. Определители n-го порядка.

В настоящей главе понятие определительобобщается максимально: будем считать порядокопределителя произвольным. Изучая определители 2-го и 3-го порядков, всё время имелась в виду целевая задача: решение системы линейных уравнений. Потом были обнаружены дополнительные возможности определителей в приложениях к задачам геометрии и физики. Так как для числа измерений больше трёх мы не можем представить себе реальных геометрических образов, то будем считать целью развития понятия определитель – решение систем линейных уравнений снеизвестными:x₁, x₂, … ,.

При переходе от определителя 2-го порядка к определителю 3-го порядка использовалось соответствие:

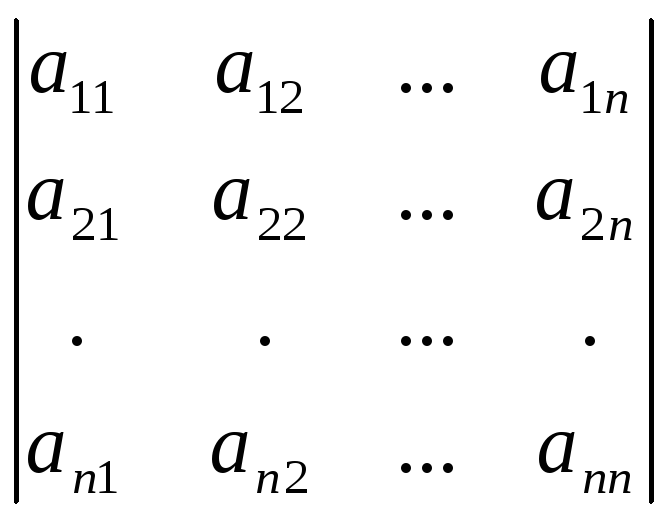квадратная матрица: A= → определитель: =|A|=d,

причём каждый член определителя должен формироваться по правилу: это произведение элементов определителя, взятых по одному из каждой строки и каждого столбца:

··…·–общий член определителя.

Число членов определителя: определяется перестановкой = n! Остаётся определить знак каждого члена определителя.

Очевидно, поиск геометрических схем определения знака члена определителя – бесперспективен! Нужно искать совсем другие схемы решения этой задачи. А значит, задачи вычисления определителя - го порядка!

§ 1. Перестановки и подстановки.

Рассмотрим множество М целых чисел: 1,2,…,n. Элементы множества М можно распо­ложить разными способами.

Определение: (3.1)

всякое расположение чисел 1,2,…,n в некотором порядке называется переста­новкой из n чисел. Общий вид записи перестановки из n элементов: ,,… ,, (1) где каждое есть одно из чисел 1,2,…,n, причем ни одно из этих чисел не встре­чается дважды и не пропущено.

В качестве можно выбрать любое из чисел 1, 2, … , n. Это дает n различных возможно­стей. Если уже выбрано, то в качестве можно выбрать лишь одно из оставшихся (n-1) чи­сел, т.е. различных способов выбрать числа (символы) и равно произведению n∙(n-1) и т.д. Число перестановок из n символов равно произведению:

Если в некоторой перестановке поменяем местами какие-либо два символа, не обяза­тельно стоящие рядом, а все остальные оставим на месте, то получим новую перестановку. Та­кое преобразование перестановки называется транспозицией.

Теорема: (3.1)

Все перестановки из n символов можно расположить в таком порядке, что каж­дая следующая перестановка получается из предыдущей одной транспозицией, причем начинать можно с любой перестановки.

►Доказательство проведем методом математической индукции. При n=2 утверждение справедливо: 1) так как: 2! = 1·2 = 2, то всего перестановок 2;

2) пусть 1-я перестановка: 1, 2 → тогда 2-я: 2, 1;

3) пусть 1-я перестановка: 2, 1 → тогда 2-я: 1, 2.

Пусть для (n-1) символов теорема выполняется. Рассмотрим все перестановки из n эле­ментов, у которых на первом месте стоит символ (не перемещается!). Таких перестановок (n-1)! и их можно (в соответствии с предположением) упорядочить так, как требует теорема. Пусть последняя из таких перестановок имеет вид:

,,… ,, (2)

В перестановке (2), содержащей n символов, совершим транспозицию символа с лю­бым другим (например, с символом ) и вновь упорядочим все перестановки из (n-1) символов при фиксированном на первом месте и т.д. Так поступим n раз. Это обеспечит пе­ребор всех n! перестановок для n символов. ◄

Следствие: от любой перестановки из n символов можно перейти к любой другой переста­новке из тех же символов при помощи нескольких транспозицией.

Если в перестановке символ стоит раньше, чем символ , но > , то говорят, что символы и составляют инверсию (нарушение порядка), иначе указанные символы составляют порядок. Перестановка называется чётной, если ее символы составляют чётное число инверсий, и нечётной – в противном случае.

Теорема: (3.2)

Всякая транспозиция меняет чётность перестановки.

►Пусть транспонируются символы: ☺ и ☻. Отметим символом ♦ те символы перестановки, которые транспозицией не затрагиваются. Рассмотрим два возможных случая:

1) перестановки имеет вид: ♦♦♦♦ ☺☻ ♦♦♦♦♦ и символы ☺ и ☻ не составляют инверсию; к выделенным символам применим одну транспозицию: ♦♦♦♦ ☻☺ ♦♦♦♦♦ → теперь сим­волы ☻ и ☺ составляют инверсию.

2) пусть перестановка записана в виде:

♦

♦

♦

☺

a1

a2

. . .

ak

☻

♦

♦

♦

♦

Транспозиций

. . .

k+1

♦

♦

♦

☻

☺

a1

. . .

ak-1

ak

♦

♦

♦

♦

. . .

k

♦

♦

♦

☻

a1

a2

. . .

ak

☺

♦

♦

♦

♦

В исходном положении символы ☺ и ☻ разделяют некоторые k символов. Если бы мы решили сразу поменять местами выделенные элементы, то не смогли бы оценить изменение их взаимоотношений с разделяющими их элементами! Поэтому берём элемент ☻, и, обмениваясь местами только с соседним левым элементом, движемся влево... На последнем шаге меняются местами выделенные элементы. Теперь имеем рядом элементы: ☻ и ☺. На такое преобразование потребовалось (k+1) транспозиций.

Для того, чтобы элемент ☺ переместился на исходное место элемента ☻, ему потребуется k транспозиций. Итак, мы обеспечили выделенным элементам транспозицию, применив 2k+1 легко учитываемых транспозиций. Так как число 2k+1 есть нечётное число, то это значит: если символы ☺ и ☻ не составляли инверсию, теперь составляют. И наоборот! ◄

Теорема: (3.3)

Сумма порядков и инверсий постоянна и равна: N =.

►Пусть исходная запись перестановки ☺: 1, 2, … , n; нарушений порядка нет. Запишем те­перь перестановку в виде ☻: n, (n-1), … , 2, 1; теперь нарушений порядка наибольшее число. От перестановки ☺ к перестановке ☻ можно перейти, используя минимальное число транспозицией: N =. Этот результат легко прочитывается из схемы, использованной при доказательстве теоремы 3.2. ◄

Анализируя рассмотренные свойства перестановок, замечаем: для формирования индексов одного из множителей общего члена определителя: ··…· требуется совместное использование двух перестановок: ,,..., и ,,...,. При этом: указывает номер строки, а номер столбца, выбираемых для выделенного множителя члена определителя. Заметим также, что для определителя удобно последовательность ,,..., заменить последовательностью: 1,2,...,n, так как в этом случае при выборе строк совсем не нужно тратить время на размышления!

Отражая выявленную потребность определителей, стали изучать специальные алгебраические конструкции – подстановки, причём исходное их определение использует две совершенно равноправные перестановки.

Определение: (3.2)

Запишем одну перестановку под другой: . Эту запись назы­вают подстановкой.

Под подстановкой понимают отображение (соответствие) множества символов, состоящего из первых n чисел: 1, 2, …, n, на себя: .

Рассмотрим пример подстановки, используя две произвольные перестановки, содержащие одни и те же элементы. .

☺☺

Пример 3–01: Пусть записана подстановка: . Что это значит?

Ответ: задано преобразование элементов (чисел) множества 1,2, … , n само на себя, а именно: 1 → 6; 2 → 5; 3 → 1; 4 → 4; 5 → 2; 6 → 3; 7 → 7; 8 → 8; 9 → 9.

☻

Из примера видим, что подстановка как отображение множества чисел 1, 2, … , n не ме­няется при транспозиции столбцов. Для приложений, ради которых мы вводим подстановки, не важен порядок столбцов подстановки. Всегда будем предполагать эквивалентность подстановок:

→, (3)

где – число, в которое переходит число .

☺☺

Пример 3–02: Почему записи: и – эквивалентны?

Ответ: обе подстановки определяют одно и то же преобразование элементов (чисел) множества 1,2, … , n само на себя, а именно: 1 → 6; 2 → 5; 3 → 1; 4 → 4; 5 → 2; 6 → 3; 7 → 7; 8 → 8; 9 → 9.

☻

Из определения эквивалентности подстановок следует, что подстановки порядка различаются только нижней перестановкой элементов. Как было показано при рассмотрении элементов комбинаторики, число различных перестановок =!

Для подстановок вводят понятия: чётная подстановка и нечётная:

▫ для записи подстановки :

- подстановка чётная, если четности верхней и нижней перестановок совпадают;

- подстановка нечётная, если четности её верхней и нижней перестановок противоположны.

▫ для записи подстановки :

- подстановка чётная, если ее определяет четная перестановка нижней строки;

- подстановка нечётная, если ее определяет нечетная перестановка нижней строки.

☺☺

Пример 3–03: Определим чётность заданной подстановки: .

Решение:

Четность подстановки определяется числом инверсий в нижней ее строке (перестановке). Для подсчета числа инверсий перестановки воспользуемся таблицей, в которой:

- символом ☻ отмечается исследуемый элемент;

- символом ♦ отмечается элемент, по отношению к которому исследуемый элемент нарушает порядок: составляет инверсию.

Видим: общее число инверсий нижней перестановки равно 5.	4	1	5	2	3
	☻	♦		♦	♦	=3
		☻				=0
			☻	♦	♦	=2
				☻		=0
	Число инверсий :						=5

Так как число 5 нечетное, то нижняя перестановка, значит и подстановка, нечетная.

☻

Кроме подсчета числа инверсий в перестановках для определения четности подстановок применяют также разложение их в циклы. Воспользуемся этим приемом (не обосновывая его, примем на веру!), рассмотрев конкретный пример.

☺☺

Пример 3–03:Определим чётность подстановки , используя разложение её в произведениециклов.

Решение:

Для иллюстрации правила формирования произвольных циклов покажем один из них, начинающийся с первого элемента верхней строки подстановки:

1	●	3	●	●	6	●	●	●	●
6	●	1	●	●	3	●	●	●	●

На этой схеме из последовательности выделен один цикл: (1→6→3→1). Запись цикла в разложении подстановки записывают в виде: (1,6,3), не повторяя второй раз элемент начала цикла.

Полное разложение подстановки в произведение циклов для рассматриваемого примера принимает вид: =,

где остающиеся на месте элементы отмечены скобками: (4), (7), (8), (9).

Имея разложение подстановки в циклы, определим число декремент: d = n – s, где n – порядок подстановки, s – число циклов в разложении подстановки. В рассматриваемом примере: d = 9 – 6 = 3 – нечетное число → подстановка нечетная.

Ответ: подстановка четная.

Пример 3–04:Имеется запись подстановки в циклах: , найти запись этой подстановки в выражении с двумя перестановками.

Решение:

Используя правила построения циклов подстановки:

1) Запишем верхнюю строку подстановки: (1 2 3 4 5).

2) Отразим в нижней строке подстановки каждый из циклов:

▫ цикл: (1 3) → (1→3→1) → (3 ● 1 ● ●);

▫ цикл: (2 5) → (2→5→2) → (● 5 ● ● 2);

▫ цикл: (4) → (4→4) → (● ● ● 4 ●).

2) Подстановка принимает вид:

Ответ: .

☻

Наблюдения: 1) Как только записан один из членов определителя: ··…·, можно записать однозначно определяемую им подстановку.

2) При выборе члена определителя однозначно определяется чётность подстановки → вопрос: А не зависит ли знак члена определителя от чётности подстановки?

Проверим гипотезу на примере определителя 3-го порядка, используя схему его вычисления в соответствии с определением:

=++–––,

Схема проверки гипотезы:

▫ для каждого члена определителя записываем соответствующую подстановку;

▫ вычисляем чётность подстановки;

▫ сопоставляем чётность-нечётность подстановки со знаками - выделенного члена определителя.

A¹: → : число инверсий в подстановке =0 → подстановка чётная → .

A²: → : число инверсий в подстановке =2 → подстановка чётная → .

A³: → : число инверсий в подстановке =2 → подстановка чётная → .

A⁴: → : число инверсий в подстановке =3 → подстановка нечётная → .

A⁵: → : число инверсий в подстановке =1 → подстановка нечётная → .

A⁶: → : число инверсий в подстановке =1 → подстановка нечётная → .

Выводы: 1) Знак члена определителя и чётность соответствующей ему подстановки взаимно однозначно соответствуют друг другу.

2) Членов определителя , столько же подстановок.

3) Среди членов определителя: отрицательных членов столько же, сколько положительных; среди подстановок нечётных столько же, сколько чётных.