§ 4. Обобщающие примеры по теме: «Кривые второго порядка».

Набор обобщающих Примеров соответствует требованиям «Семестрового плана» при изучении темы: «Кривые второго порядка». Эти Примеры предназначены закрепить навыки применения общих алгоритмов решений, установленных в поясняющих Примерах.

☺ ☻ ☺

Пример 1–444: Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметричного относительно начала координат, зная кроме того, что:

1) его полуоси равны 5 и 2;

2) его большая ось равна 10, а расстояние между фокусами 2= 8;

3) его малая ось равна 24, а расстояние между фокусами 2= 10;

4) расстояние между фокусами 2= 6 и эксцентриситет =;

5) его большая ось равна 20, а эксцентриситет =;

6) его малая ось равна 10, а эксцентриситет =;

7) расстояние между его директрисами равно 5, между фокусами 2= 4;

8) его большая ось равна 8, а расстояние между директрисами равно 16;

9) его малая ось равна 6, а расстояние между директрисами равно 13;

10) расстояние между его директрисами равно 32 и эксцентриситет =.

Решение:

Общее: воспользуемся рисунком и основными выражениями для эллипса:

уравнение: , – большая полуось, – малая полуось, =–, где – фокус; – эксцентриситет; =, =; +=2, – директриса.

Учитывая принятые обозначения, а также указанные основные соотношения между элементами эллипса, последовательно решаем все задания:

1). В соответствии с принятыми обозначениями запишем: =5, = 2, и каноническое уравнение эллипса принимает вид .

2). Из условия: 2=10 и 2= 8 → =5; =4. Тогда =–=9 и уравнение эллипса: .

3). Из условия: 2=24 и 2=10 → =12; =5. Тогда =+=169 и можем записать уравнение эллипса .

4). Из условия: 2=6 и ==→ =3, . Далее =–=16 и можем записать уравнение эллипса .

5). Из условия: 2=20 и == → =10; =·=6. Далее =–=64 и можем записать уравнение эллипса .

6). Из условия: 2=10 и == → =5 и имеем систему: откуда: =169 и следует уравнение эллипса .

7). Из условия: 2=2=5 и =2 → получаем (используя =·=2) систему: откуда вычисляем: = 5 и =–= 1, тогда уравнение эллипса: .

8). Из условия: 2=8 и 2=2=16 → = 4 и =, далее =·=2 и =–=12, после чего уравнение эллипса: .

9). Из условия: 2=6 и 2==13 → = 3 и =. Из формулы =· → =·=. Учтем также: =–=–9, получаем биквадратное уравнение: =–9, откуда =13 и =. Варианты записи уравнений эллипса: .

10). Из условия: 2=2=32 и = → =8 и =·=4. Далее вычисляем =–=48 и записываем уравнение эллипса .

Ответ: для случаев: 1) , 2) , 3) , 4) .

5) , 6) , 7) , 8) .

, ; 10) .

Пример 2–452: Пользуясь одним циркулем, построить фокусы эллипса (считая, что изображены оси координат и задана масштабная единица).

Решение:

1). В соответствии с уравнением имеем отрезки =4 и =3. Это значит, определены большая и малая полуоси эллипса, и их координаты можно отметить на осях . Координаты фокусов можно было бы вычислить по формуле: =–.

2). Из выражения =– следует, что отрезки и можно считать катетами прямоугольного треугольника, а отрезок – гипотенузой. Отсюда следует последовательность построений: на оси отмечаем точку (0,). На одной из осей координат циркулем снимаем размер отрезка =4, и из точки (0, ) радиусом = отмечаем точки (–, 0)и (, 0).

Ответ: обоснование и последовательность действий: в тексте, рисунок показан.

Пример 3–465: Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если даны:

1) точка (–2, 2) эллипса и его малая полуось =2;

2) точка (2, –2) эллипса и его большая полуось =4;

3) точки (4, –) и (2, 3) эллипса;

4) точка (, –1) эллипса и расстояние между его фокусами 2= 8;

5) точка (2, –) эллипса и его эксцентриситет = ;

6) точка (8, 12) эллипса и расстояние = 20 от нее до левого фокуса;

7) точка (–, 2) эллипса и расстояние между его директрисами, равное 10.

Решение:

Учитывая принятые обозначения, а также основные соотношения между элементами эллипса, последовательно решаем все задания:

1). Так как точка принадлежит эллипсу, то: , откуда =36. Получаем уравнение эллипса .

2). Так как точка принадлежит эллипсу, то: , откуда =. Получаем уравнение эллипса .

3). Так как точка принадлежит эллипсу, то ; точка также принадлежит эллипсу ; решая полученную систему уравнений, получаем: =20, =15. Получаем уравнение эллипса .

4). Так как точка принадлежит эллипсу, то: , из 2= 8 имеем 16 =–. решая полученную систему уравнений, получаем: a² =20, b² =4 и записываем уравнение эллипса .

5). Так как точка принадлежит эллипсу, то: . Учитывая , а также =–, получаем =. Решая полученную систему уравнений, имеем: =9, =5 и записываем уравнение эллипса .

6). Так как точка принадлежит эллипсу, то: . Из ==20 для точки получаем =20, или 8=20–. Учитывая =–, получаем систему уравнений:

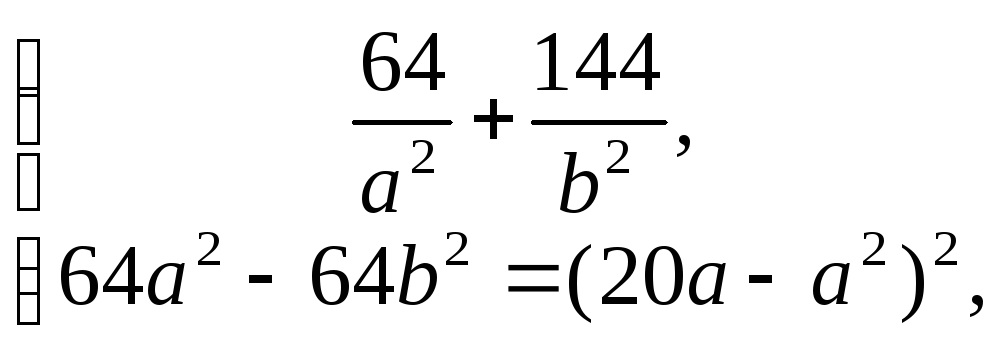откуда: =256, =192 → ответ: .

7). Так как точка принадлежит эллипсу, то:. Из 2===10 запишем: =5. Учитывая =–, получаем систему уравнений:

откуда: =15, =6 → ответ: .

Ответ: для случаев: 1) , 2) , 3) , 4) .

5) , 6) , 7) .

Пример 4–507: Направляющей круглого цилиндра является окружность радиуса = 8. Определить полуоси эллипса, полученного в сечении этого цилиндра плоскостью, наклоненной к его оси под углом = 30⁰ .

Решение:

Замечание: представление цилиндра видом сбоку наиболее удобно, так как в этом случае мы видим большую ось эллипса неискажённой; то, что малая ось эллипса представлена точкой не вызывает особых неудобств.

1). Сечение цилиндра плоскостью есть окружность. Очевидно, меньшая полуось эллипса равна == 8.

2). Большая ось эллипса расположена в сечении : мы её видим неискажённой. Из прямоугольного треугольника вычисляем = .

Ответ: меньшая полуось: 8, большая: 16.

Пример 5–515: Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, что:

1) ее оси равны 2= 10, 2= 8;

2) расстояние между фокусами 2=10 и ось 2= 8;

3) расстояние между фокусами 2= 6 и эксцентриситет ;

4) ось 2=16 и эксцентриситет =;

5) уравнения асимптот: = а расстояние между фокусами 2= 20;

6) расстояние между ее директрисами равно (в Задачнике ошибка!) и расстояние между фокусами 2= 26;

7) расстояние между ее директрисами равно и ось 2b = 6;

8) расстояние между ее директрисами равно и эксцентриситет =;

9) уравнения асимптот = ± и расстояние между директрисами равно .

Решение:

Общее: воспользуемся рисунком и основными выражениями для гиперболы:

уравнение линии: , – вещественная полуось, – мнимая полуось гиперболы. Для вычисления фокусов гиперболы используется выражение: =–, где – фокус.

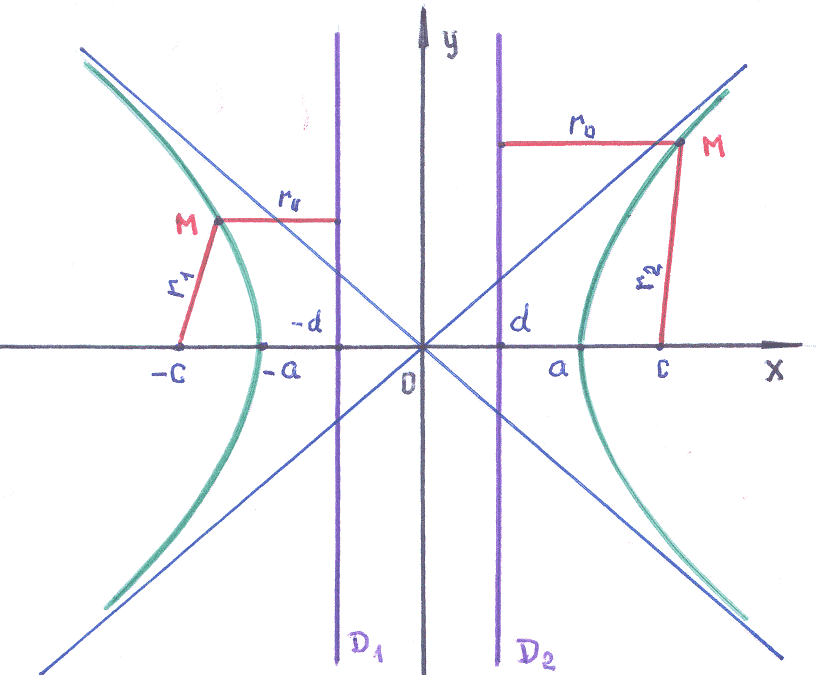Эксцентриситет гиперболы: . Левая ветвь: =, =. Правая ветвь: =, =. В каждом случае: =2. Директриса: . Асимптоты: = ± .

Учитывая принятые обозначения, а также указанные основные соотношения между элементами гиперболы, последовательно решаем все задания:

Решение:

1). Из условия: 2=10, 2=8 → =5, =4, и каноническое уравнение гиперболы: .

2). Из условия: 2=8 и 2=10 → =4; =5. Тогда =–= 9 → гипербола: .

3). Из условия: 2=6 и == → =3 и =2. Тогда =–=5 → гипербола: .

4). Из условия: 2=16 и == → =8 и =·=10. Тогда =–=36 → записываем уравнение .

5). Из условия: 2=20 и = → =10 и 3=4. Тогда =–=100–. Из полученных уравнений (системы) получаем: =36 и =64 → гипербола .

6). Из условия: 2=26 и 2=2=2= → =13 и =144. Далее =–=25 → гипербола: .

7). Из условия: 2=6 и 2=2=2= → =3 и =. Учитывая =–, получаем уравнение: 9 =–, откуда (положительный корень!) =5. Далее находим: =16 и записываем уравнение гиперболы: .

8). Из условия: 2=2= и == → откуда =2 и =· =3. Тогда =–=5 и записываем уравнение: .

9). Из условия: = и 2=2=2= → = и . Учитывая =–, получаем уравнение: =– или с=–откуда (положительный корень!) =10. Следует: =64 → =36 и записываем уравнение: .

Ответ: случаи: 1) , 2) , 3) , 4) , 5) .

6) , 7) , 8) , 9) .

Пример 6–520: Вычислить площадь треугольника, образованного прямой : и асимптотами гиперболы .

Решение:

1). Вспомним общее выражение для асимптот гиперболы: = ± . Из условий и в соответствии с рисунком имеем уравнения асимптот : =, : = –.

2). Координаты выделенных точек: (2,3), (4,6), найдены как точки пересечения соответствующих прямых.

3). Вычисление площади треугольника : выполнено с использованием простейшей формулы: =[основание]·[высота].

Ответ: площадь треугольника: =12.

Пример 7–530: Через левый фокус гиперболы проведен перпендикуляр к ее оси, содержащей вершины. Определить расстояние от фокусов до точек пересечения этого перпендикуляра с гиперболой.

Решение:

1). Используя заданное уравнение гиперболы, учитывая выражение: =+=169, определяем фокус = 13. Используя выражение для эксцентриситета: =, вычисляем =.

2). Для левой ветви гиперболы выделена точка такая, что =–=–13. Для этой точки, используя общие формулы, имеем: =. В нашем примере: = –·(–13) –12 = .

Аналогично вычисляем расстояние точки до второго фокуса ==–·(–13)+12 =.

Ответ: расстояние от фокусов = ; = .

Пример 8–566: Гипербола проходит через точку (,3) и касается прямой . Составить уравнение этой гиперболы при условии, что ее оси совпадают с осями координат.

Решение:

1). Так как точка принадлежит гиперболе, то: . Пусть , тогда .

2). При исследовании свойств линий 2-го порядка было получено выражением для углового коэффициента касательной к гиперболе в некоторой точке , именно: =. Из заданного уравнения касательной имеем: =. Видим, точка не принадлежит заданной касательной! Приравнивая коэффициенты , имеем: =. Учитывая: и , получим: =.

3). Так как точка принадлежит касательной, то дополнительно имеем: . Решая систему уравнений: получаем и .

4). Так как точка принадлежит гиперболе, то необходимо: . Умножим это равенство на число (6·9) и учтем и . Получаем: , или . Подставляя в него из п. 3), применив необходимые упрощения, получаем квадратное уравнение: . Его корни (по Виету!): =, =.

5). Для значения получаем: , → гипербола: , Для значения , аналогично, находим гиперболу: .

Ответ: уравнения гипербол: и .

Замечание: пример 8 иллюстрирует возможности получения необходимых геометрических свойств: в рассматриваемом примере требовалось расположить гиперболу в ограниченном пространстве.

Пример 9–583: Составить уравнение параболы, вершина которой находится в начале ординат, зная, что:

1) парабола расположена в правой полуплоскости симметрично относительно оси и ее параметр = 3;

2) парабола расположена в левой полуплоскости симметрично относительно оси и ее параметр = 0.5;

3) парабола расположена в верхней полуплоскости симметрично относительно оси и ее параметр = ;

4) парабола расположена в нижней полуплоскости симметрично относительно оси и ее параметр = 3.

Решение:

Общее: воспользуемся рисунком и основными выражениями для параболы:

уравнение линии: , фокус: , эксцентриситет: ==1, расстояние от произвольной точки до фокуса: , директриса: =.

Учитывая принятые обозначения, а также указанные основные соотношения между элементами гиперболы, последовательно решаем все задания:

1). Из условия: каноническое уравнение параболы: и =3 → тогда: .

2). Из условия: каноническое уравнение параболы: и =0.5 → тогда: .

3). Из условия: каноническое уравнение параболы: и = → тогда: .

4). Из условия: каноническое уравнение параболы: и =3 → тогда: .

Ответ: случаи: 1) , 2) , 3) , 4) .

Пример 10–588: Установить, какие линии определяются следующими уравнениями: 1) ; 2) ; 3) ; 4) .

Решение:

Можно было бы воспользоваться сведениями из элементарной алгебры и построить все графики заданных линий. Мы воспользуемся каноническими уравнениями линий 2-го порядка.

1). Отметим, прежде всего, область определения функции первого случая: . Область значений исходной функции: положительная полуось , то есть: .

Возведём в квадрат заданное равенство. Получится каноническое уравнение параболы: .

Из канонического уравнения следует, что уравнение директрисы: . Координаты фокуса параболы: (1,0). Окончательно запишем: для значений .

График функции иллюстрирует основные элементы параболы рассматриваемого случая, причём учтена область значений исходной записи уравнения функции.

2). Для функции второго случая: область определения: . Область значений исходной функции: положительная полуось , то есть: .

Возведём в квадрат заданное равенство. Получится каноническое уравнение параболы:

.

Из канонического уравнения следует, что уравнение директрисы: . Координаты фокуса параболы: (1,0). Окончательно запишем: для значений .

График функции иллюстрирует основные элементы параболы рассматриваемого случая.

3). Для функции третьего случая : область определения: . Область значений исходной функции: отрицательная полуось , то есть: .

Возведём в квадрат заданное равенство. Получится каноническое уравнение параболы:

.

Из канонического уравнения следует, что уравнение директрисы: . Окончательно запишем: для значений .

График функции иллюстрирует основные элементы параболы рассматриваемого случая.

4). Для функции четвёртого случая : область определения: . Область значений исходной функции: отрицательная полуось , то есть: .

Возведём в квадрат заданное равенство. Получится каноническое уравнение параболы:

.

Из канонического уравнения следует, что уравнение директрисы: . Окончательно запишем: для значений .

График функции иллюстрирует основные элементы параболы рассматриваемого случая.

Ответ: подробный анализ функций представлен в тексте, рисунки в тексте.

Пример 11–592: На параболе y² = 16x найти точки, фокальный радиус которых равен 13.

Решение:

1). Воспользуемся каноническим уравнением параболы: . Из заданного уравнения имеем: .

2). Учитывая, что для любой точки, расположенной на параболе имеем: , запишем: , откуда вычисляем: . Так как точка расположена на параболе, получаем: . Получены точки: (9, –12), (9, 12).

Ответ: точки: (9, –12), (9, 12).

Пример 12–598: Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершины и величину параметра : 1) ; 2) ; 3) x =–y²+2 y –1.

Решение:

1). Применим выделение полного квадрата: или . Это значит, координаты вершины параболы (–4,3), параметр = .

2). Применим выделение полного квадрата: . Последнее запишем в виде: . Это значит, координаты вершины параболы (2,1), параметр = 2.

3). Преобразуем запись функции: =. Это значит, координаты вершины параболы (0,1), параметр =.

Ответ: случаи: 1) (–4,3), = ; 2) (2,1), = 2; 3) (0,1), =.

☻

Вопросы для самопроверки:

1. Что такое окружность, эллипс?

2. Что такое гипербола?

3. Что такое парабола?

4. Что такое эксцентриситет кривой второго порядка?

5. Что такое директриса для кривой 2-го порядка?

6. Что такое диаметр кривой 2-го порядка?

7. Как получают уравнения касательных к кривым 2-го порядка?

8. Какие свойства касательных кривых 2-го порядка определяют их особые оптические свойства?

9. Какие кинематические свойства эллипса показались наиболее привлекательными?

10. Чем примечательны уравнения кривых 2-го порядка в полярных координатах?

11. Чем вызвана необходимость введения обобщённых полярных координат?

Задачи для самоподготовки:

Пример 1–445: Составить уравнение эллипса, фокусы которого лежат на оси ординат, симметричного относительно начала координат, зная кроме того, что:

1) его полуоси равны 7 и 2;

2) его большая ось равна 10, а расстояние между фокусами 2= 8;

3) расстояние между фокусами 2= 24 и эксцентриситет =;

4) его малая ось равна 16, а эксцентриситет =;

5) расстояние между фокусами 2= 6 и расстояние между его директрисами равно ;

6) расстояние между его директрисами равно и эксцентриситет =.

Ответ: для случаев: 1) , 2) , 3) , 4) ,

5) , 6) .

Пример 2–455: Установить, какие линии определяются следующими уравнениями, и изобразить эти линии на чертеже:

1) ; 2) ; 3) ; 4) .

Ответ: для случаев: 1) – эллипс:; 2) – эллипс: .

3) – эллипс:; 4) – эллипс: .

Пример 3–466: Определить эксцентриситет эллипса, если:

1) его малая ось видна из фокусов под углом 60⁰;

2) отрезок между фокусами виден из вершин малой оси под прямым углом;

3) расстояние между директрисами в 3 раза больше расстояния между фокусами;

4) отрезок перпендикуляра, опущенного из центра эллипса на его директрису, делится вершиной эллипса пополам.

Ответ: для случаев: 1) ==, 2) ==, 3) ==, 4) ==.

Пример 4–508: Направляющей круглого цилиндра является окружность радиуса =. Определить, под каким углом к оси цилиндра нужно его пересечь, чтобы в сечении получить эллипс с большой полуосью =2.

Ответ: угол: = 60⁰.

Пример 5–516: Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, что:

1) ее полуоси равны = 6, = 18;

2) расстояние между фокусами 2 =10 и эксцентриситет =;

3) уравнения асимптот: а расстояние между вершинами 2=48;

4) расстояние между ее директрисами равно и эксцентриситет =;

5) уравнения асимптот: , расстояние между ее директрисами равно .

Ответ: для случаев: 1) , 2) , 3) ,

4) , 5) .

Пример 6–521: Установить, какие линии определяются следующими уравнениями, и изобразить эти линии на чертеже:

1) ; 2) ; 3) ; 4) .

Ответ: для случаев: 1) – гипербола:; 2) – гипербола: .

3) – гипербола: ; 4) – гипербола: .

Пример 7–531: Пользуясь одним циркулем, построить фокусы гиперболы (считая, что изображены оси координат и задана масштабная единица).

Ответ: для построения фокуса необходимо учесть зависимость .

Пример 8–567: Составить уравнение гиперболы, касающейся прямых: l₁: и l₂: при условии, что ее оси совпадают с осями координат.

Ответ: каноническое уравнение гиперболы: .

Пример 9–585: Составить уравнение параболы, вершина которой находится в начале ординат, зная, что:

Решение:

1) парабола расположена симметрично относительно оси и проходит через точку (9,6);

2) парабола расположена симметрично относительно оси и проходит через точку (–1,3);

3) парабола расположена симметрично относительно оси и проходит через точку C(1,1);

4) парабола расположена симметрично относительно оси и проходит через точку (4,–8).

Ответ: для случаев: 1) , 2) , 3) , 4) .

Пример 10–589: Найти фокус F и уравнение директрисы параболы: .

Ответ: фокус (6,0) и уравнение директрисы: =–6.

Пример 11–593: Составить уравнение параболы, если (–7,0) и уравнение директрисы: = 7.

Ответ: уравнение параболы: .

Пример 12–596: Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершины , величину и уравнение директрисы:

1) ; 2) ; 3) ; 4) .

Ответ: для случаев: 1) вершины параболы: (2,0); =2; уравнение директрисы: .

2) вершины параболы: ; =3; уравнение директрисы: .

3) вершины параболы: ; =3; уравнение директрисы: .

4) вершины параболы: (0,2); =; уравнение директрисы: .

< * * * * * >