§ 8. Прямолинейные образующие поверхностей второго порядка.
При рассмотрении конических и цилиндрических поверхностей легко заметить, что эти поверхности образованы движением прямой линии. Движение применялось простейшее: вращение вокруг неподвижной оси.
Рисунки поверхностей однополостного гиперболоида и гиперболического параболоида не подсказывают, что эти поверхности могут быть построены за счёт какого-то, пусть даже сложного, движения прямолинейных образующих: ведь это значило бы, что какие-то прямые целиком лежат на этих поверхностях!
Не будем делать выводов, применяя только впечатления от восприятия формы геометрических фигур. Применим логически оправданные действия. Если допустить, что прямая линия принадлежит какой-то поверхности, необходимо, выполнить действия:
▫ взять
произвольную точку
,
принадлежащую исследуемой поверхности;
▫ взять
прямую линию, проходящую через точку
,
и определяемую общими уравнениями;
▫ доказать, что за счёт выбора значений общих параметров прямой можно добиться того, что прямая линия целиком принадлежит поверхности.
Пусть
уравнение прямой задано параметрическими
уравнениями
:
Из этих уравнений следует: точка
принадлежит прямой линии, направление
прямой определяет вектор
=
.
У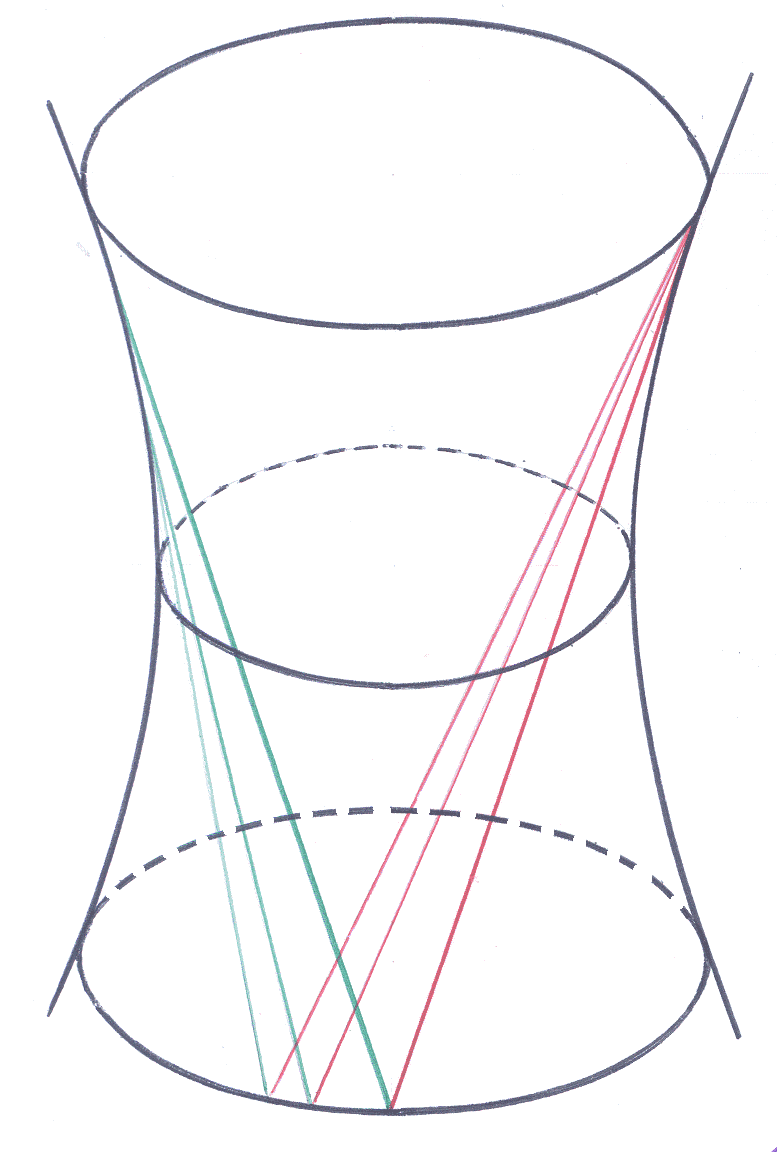
читывая,
что любые преобразования прямоугольных
координат не изменяют геометрические
фигуры, расположенные в пространстве,
станем использовать такую систему
координат, в которой рассматриваемая
фигура определяется простейшим
алгебраическим выражением: каноническим
уравнением.
Однополостный
гиперболоид.
Его каноническое уравнение:
.
Для упрощения записи используемых
алгебраических выражений запишем
уравнение поверхности в виде:
.
Пусть
точка
принадлежит поверхности однополостного
гиперболоида. Так как прямая должна
принадлежать его поверхности, то точка
также должна принадлежит рассматриваемой
поверхности. Подставим значения
переменных:
из параметрических уравнений прямой в
каноническое уравнение поверхности.
Получим уравнение 2-го порядка относительно
переменной
:
,
(1)
где коэффициенты могут быть записаны в виде выражений:
=
;
=
; 
=
.
Если
прямая линия
принадлежит рассматриваемой поверхности,
то уравнению (1) удовлетворяют любые
значения
.
Возьмём три различных значения переменной
:
.
Для этих значений получим систему
уравнений:
определитель
этой системы:
=
0.
Так как
система трёх линейных однородных
уравнений относительно неизвестных
,
,
имеет определитель, не равный нулю, то
её единственным решением является
нулевое решение:
=0,
=0,
=0.
Верно
и обратное. Если коэффициенты уравнения
(1)
=0,
=0,
=0,
то оно удовлетворяется любыми значениями
.
В нашем случае это значит, что прямая
линия
принадлежит поверхности:
.
Применим
полученный результат к однополостному
гиперболоиду. Учтём сразу, что на его
поверхности значения
,
,
не могут быть равны нулю одновременно.
Пусть
0.
Из
условия
=0
следует:
.
Тогда можем записать:
=
=0. (2)
Координаты
вектора
=
не могут быть равны нулю одновременно.
Из условия
=0
мы получили бы одновременно:
=0.
Последнее невозможно, так как
0.
Пусть
0.
Применяя несложные алгебраические
преобразования, равенство (2) можем
записать в виде выражения: 
=0. (3)
Решая
квадратное уравнение (3) относительно
отношения
,
запишем решение в виде:
=
. (4)
Так как
=
=0,
то
и выражение (4) ещё более упростится: 
=
(5)
Из
выражения (5) следует: для существования
действительных решений уравнения (3)
необходимо и достаточно, чтобы выполнялось
условие:
<
0. Возможны следующие комбинации
знаков в уравнении (1):
|
|
A |
B |
C |
|
I |
– |
– |
– |
|
II |
+ |
+ |
– |
В случае I уравнение (1) определяет мнимый эллипсоид – прямолинейных образующих не имеет. В случае II уравнение (1) определяет однополостный гиперболоид – прямолинейные образующие имеет.
Так как
для однополостного гиперболоида
0,
то для каждой точки
имеем две прямолинейные образующие (на
рисунке показаны разным цветом).
Учитывая,
что для однополостного гиперболоида
имеем:
=
,
=
,
=–
,
получаем выражения:
=
=
. (6)
Учитывая
выражение (6), и используя выражение
,
получим полную характеристику необходимого
для точки
вектора
:
=
. (7)
Если в
выражении (6) выбирать всё время знак
,
будем получать прямолинейные образующие
поверхности одного семейства. Знаку
будет соответствовать второе семейство
образующих той же поверхности.
Важно
то, что
.
Это значит, что
0,
то есть никакая прямолинейная образующая
не параллельна плоскости координат
.
Из этого следует, что все образующие
однополостного гиперболоида пересекают
горловой
эллипс:
По поводу прямолинейных образующих однополостного гиперболоида полезно знать две теоремы (из рисунка вполне можно видеть намёк-подтверждение!).
|
Теорема: (6.1) |
Две прямолинейные образующие, принадлежащие различным семействам, всегда лежат в одной плоскости, и параллельны тогда и только тогда, когда проходят через диаметрально противоположные точки горлового эллипса. |
►Пусть
имеем две прямолинейные образующие
и
,
принадлежащие различным семействам.
Пусть
пересекает горловой эллипс в точке
,
а
– в точке
.
Если
точки
и
совпадают, то утверждение очевидно.
Пусть теперь точки
и
различны. Учтём, что для горлового
эллипса
=0
и
.
В этом случае имеем:
=
и
=–
или
=
. (8)
и
одновременно: 
=
. (9)
Обозначим
векторы
=
,
=
и
.
Условием принадлежности образующих
и
одной плоскости является:
=0.
Из
выражений (8) и (9) видно, что векторы
и
только в случае, когда
и
проходят через диаметрально противоположные
точки горлового эллипса:
=
,
=
,
=
=0.
Теорема доказана! ◄
Замечание: если детали доказательства теоремы применить к тому же рисунку, то нетрудно признаться себе, что интуиция – только помощница при доказательстве теорем, но не само доказательство!
теоремы (из рисунка вполне можно видеть намёк-подтверждение!).
|
Теорема: (6.2) |
Любые две прямолинейные образующие одного семейства не принадлежат одной плоскости. |
►Пусть
имеем две прямолинейные образующие
и
,
которые принадлежат одному семейству
и пересекают горловой эллипс в точке
и в точке
,
соответственно. Точки
и
различны, иначе образующие совпадали
бы!
В этом случае имеем:
=
и 
=
. (10)
Вычисления
показывают, что на этот раз:
0.
Из этого следует, что
и
– скрещивающиеся прямолинейные
образующие однополостного гиперболоида.
Теорема доказана! ◄
Используя
результаты теорем, можно попробовать
найти прямолинейные образующие
однополостного гиперболоида, выполняя
формальные алгебраические действия с
исходным выражением
:
→ 
. (11)
Используя (11), запишем уравнения прямых линий:
и
(12)
Нетрудно
заметить, учитывая (11), что при любых
значениях чисел:
и
прямые
и
лежат на поверхности однополосного
гиперболоида: для этого достаточно
перемножить первое и второе уравнения
для системы
,
аналогично для системы
.
Формальное использование уравнений (12) полезно тем, что эти уравнения могут быть легко записаны. Конечно, способ, опирающийся на выражения (11) и (12), не отменяет важность доказанных теорем!
Интересно: Однополостные гиперболоиды используют при сооружении прочных, лёгких и простых в изготовлении башен. Такую конструкцию предложил русский инженер Шухов В.Г. (1853-1939). В соответствии с его идеей построена Останкинская телебашня в Москве (каждый может ею полюбоваться!).
☺☺
Пример 6–16:
Для однополостного гиперболоида:
найти прямолинейные образующие,
проходящие через точку
(3,2,1).
Решение:
1). Запишем
исходное выражение в виде:
,
откуда уравнения прямолинейных образующих
можно записать в виде:
и
2).
Подставляя в полученные уравнения
координаты заданной точки
(3,2,1),
получаем: из уравнений системы
:
,
причём 
–
произвольное число, а для системы
:
–
произвольное число и 
=0.
Используя полученные значения пар 
и 
,
запишем уравнения образующих:
и
Ответ: уравнения
образующих:
и
Замечание: Используя полученные уравнения, без особого труда можно получить параметрические уравнения образующих (ведь именно с их помощью была решена рассмотренная задача).
☻
Г
иперболический
параболоид.
Его каноническое уравнение:
.
Для упрощения записи используемых
алгебраических выражений запишем
уравнение поверхности в виде:
.
Пусть
точка
принадлежит поверхности однополостного
гиперболоида. Так как прямая должна
принадлежать его поверхности, то точка
также должна принадлежит рассматриваемой
поверхности. Подставим значения
переменных:
из параметрических уравнений прямой в
каноническое уравнение поверхности.
Получим уравнение 2-го порядка относительно
переменной
:
,
(1)
где коэффициенты могут быть записаны в виде выражений:
=
;
=
; 
=
.
Если
прямая линия
принадлежит рассматриваемой поверхности,
то уравнению (1) удовлетворяют любые
значения
.
Возьмём три различных значения переменной
:
.
Для этих значений получим систему
уравнений:
определитель
этой системы:
=
0. (2)
Так как
система трёх линейных однородных
уравнений относительно неизвестных
,
,
имеет определитель, не равный нулю, то
её единственным решением является
нулевое решение:
=0,
=0,
=0.
Верно
и обратное. Если коэффициенты уравнения
(1)
=0,
=0,
=0,
то оно удовлетворяется любыми значениями
.
В нашем случае это значит, что прямая
линия
принадлежит поверхности:
.
Используя
условия:
=0,
=0,
=0,
как и в случае однополостного гиперболоида,
получаем: 
=
и 
=
. (3)
Так как
имеет действительные значения только
в случае, если числа
и
имеют разные знаки, то есть:
,
то это имеет место только в случае
гиперболического параболоида.
Из формул
(3) видно, что через каждую точку поверхности
проходит две прямолинейные образующие,
принадлежащие к различным семействам.
Так как
постоянная величина, то в каждой точке
поверхности одна из прямолинейных
образующих параллельна плоскости
,
а другая плоскости
,
причём
>0,
<
0. Это значит, что образующие одного
семейства параллельны одной плоскости,
а образующие другого параллельны другой
плоскости.
Как и в случае однополостного гиперболоида, можно показать, что две прямолинейные образующие одного семейства не принадлежат одной плоскости, а две прямолинейные образующие различных семейств пересекаются. Нетрудно также получить прямолинейные образующие, непосредственно используя уравнение поверхности:
. (4)
Используя (4), запишем уравнения прямых линий:
и
(5)
Прямолинейные
образующие
и
принадлежат поверхности гиперболического
параболоида.
☺☺
Пример 6–17:
Убедившись, что точка
(1,3,–1)
лежит на гиперболическом параболоиде:
,
составить уравнения его прямолинейных
образующих, проходящих через точку
.
Решение:
1). Запишем
уравнение гиперболического параболоида
в виде:
.
2). Запишем уравнения прямолинейных образующих для заданной поверхности:
и
3).
Проверка того, что точка
принадлежит поверхности, делается
устно!
Подставляя в полученные уравнения
координаты заданной точки
(1,3,–1),
получаем:
▫ для
образующей
соотношение
;
▫ для
образующей
соотношение
.
4).
Используя
полученные значения пар 
и 
,
запишем уравнения образующих:
:
и
:
5). Найдём
канонические уравнения образующей
:
▫ из
системы выделяем произвольную точку,
принадлежащую
:
(0,–1,1);
▫ используя
нормали:
=(2,
–1,
–1),
=(2,0,
1) плоскостей, вычисляем направляющий
вектор образующей:
=
×
=(1,4,–2).
▫ записываем
каноническое уравнение образующей:
.
6). Найдём
канонические уравнения образующей
:
▫ из
системы выделяем произвольную точку,
принадлежащую
:
(0,–9,
–3);
▫ используя
нормали:
=(2,
0,–1),
=(6,–1,
3) плоскостей, вычисляем направляющий
вектор образующей:
=
×
=(1,
12, 2).
▫ записываем
каноническое уравнение образующей:
.
Ответ: уравнения
образующих
:
и
:
.
Замечание: Используя полученные уравнения, без особого труда можно получить параметрические уравнения образующих (ведь именно с их помощью была решена рассмотренная задача).
☻
Исследование свойств поверхностей 2-го порядка полезно не только потому, что эти поверхности всегда привлекали изяществом своих форм. Эти поверхности великолепны ещё и своими механическими свойствами: их прочность изумительна!
В
спомним
давнюю пасхальную шутку на Руси:
предлагают известному своей силой Ване
попытаться раздавить куриное яйцо (чаще
это пасхальное яйцо!). Силач, сцепив
пальцы рук, начинает сжимать его между
ладоней. Доверчивым силачам (и высокого
мнения о своей силе!) кажется, что работа
займёт несколько секунд!..
На самом деле, редко кому удаётся подтвердить свою безграничную силу! Обычно успех бывает только в случае, если яйцо имеет дефекты. Или силач хитрил: усилия прикладывались несимметрично!
Вспомним ещё изящную форму фюзеляжа самолёта, корпус подводной лодки! У них внутри спрятаны цилиндрические шпангоуты: лёгкие, но очень прочные!