
§ 3. Ранг системы n- векторов и матрицы.
Для ответа на
поставленный вопрос требуется продолжить
исследование пространства
![]() .
.
Рассмотрим
системы векторов:![]() ,
,![]() ,...,
,...,![]() , (A)
, (A)
![]() ,
,![]() ,...,
,...,![]() . (B)
. (B)
![]() ,
,![]() ,...,
,...,![]() . (C)
. (C)
Если система (B) выражается линейно через систему (А), а система (C) через систему (B), то система (C) линейно выражается через систему (А) – транзитивность понятия: линейно выражается.
Две системы векторов эквивалентны, если каждая из них может быть линейно выражена через другую – транзитивность понятия эквивалентности.
Замечание: если одна из двух эквивалентных между собой систем векторов независима, то не обязательно этим свойством обладает и другая!
|
Теорема: (6.2) |
Если
в
причем
система (А)
линейно
независима
и
линейно выражается через систему
(B),
то
число векторов в
(А)
не
больше, чем в (B),
то
есть
|
►Доказательство.
Пусть (А)
линейно независима и линейно выражается
через (B),
но
![]() >
>![]() :
:
![]() =
=![]() +
+![]() +
… +
+
… +![]() ,
,
![]() =
=![]() +
+![]() +
… +
+
… +![]() ,
,
. . . . . . . . . . . . . . . . (7)
![]() =
=![]() +
+![]() +
… +
+
… +![]() ,
,
где
![]() ,
,
![]() ;
;
![]() –
вещественные числа.
–
вещественные числа.
Из
коэффициентов уравнений (7) составим
![]() -мерные
векторы:
-мерные
векторы:
![]() =
(
=
(![]() ,
,![]() ,...,
,...,![]() ),
),
![]() =
(
=
(![]() ,
,![]() ,...,
,...,![]() ),
),
. . . . . . . . . . . . (8)
![]() =
(
=
(![]() ,
,![]() ,...,
,...,![]() ).
).
Так
как
![]() >
>![]() (по допущению), то, в соответствии с
теоремой 6.1, система векторов (8) линейно
зависима:
(по допущению), то, в соответствии с
теоремой 6.1, система векторов (8) линейно
зависима:
![]() ·
·![]() +
+![]() ·
·![]() +
…+
+
…+![]() ·
·![]() =0, (9)
=0, (9)
то
есть хотя бы один из коэффициентов
![]() ,
,
![]() ,…,
,…,
![]() не равен нулю. Из выражений (8) и (9)
следует:
не равен нулю. Из выражений (8) и (9)
следует: ![]()
![]() +
+![]()
![]() +
… +
+
… +![]()
![]() =0,
=0,
![]()
![]() +
+![]()
![]() +
… +
+
… +![]()
![]() =0, (10)
=0, (10)
. . . . . . . . . . . . . . .
![]()
![]() +
+![]()
![]() +
… +
+
… +![]()
![]() =0.
=0.
Для
удобства использования системы (10)
запишем её в компактной форме:
![]() =0,
j
= 1,2,…,
=0,
j
= 1,2,…,![]() .
Используя систему векторов (A),
составим линейную комбинацию:
.
Используя систему векторов (A),
составим линейную комбинацию:
![]() ·
·![]() +
+![]() ·
·![]() +
…+
+
…+![]() ·
·![]() ,
(11)
,
(11)
Для
удобства, выражение (11) также
запишем в компактной форме:
![]() и преобразуем:
и преобразуем:
![]() =(1)=
=(1)= =(2)=
=(2)= =(3)=0
=(3)=0
Выполнены
операции:
(1):
учтены линейные комбинации (7). (2):
меняем порядок суммирования по индексам
![]() в двойной сумме. (3):
учитываем:
в двойной сумме. (3):
учитываем:
![]() =0,
j
= 1,2,…,
=0,
j
= 1,2,…,![]() .
.
Последняя
запись противоречит линейной независимости
системы векторов (А),
и значит необходимо:
![]() ≤
≤
![]() .
◄
.
◄
Следствие –1 теоремы 6.2:
– всякие
две эквивалентные
линейно независимые
системы векторов в
![]() -мерном
пространстве содержат равное
число
векторов;
-мерном
пространстве содержат равное
число
векторов;
– любые
две максимальные
линейно независимые
системы
![]() -мерных
векторов
-мерных
векторов
![]() -мерного
пространства состоят из
одного
и того же числа векторов.
-мерного
пространства состоят из
одного
и того же числа векторов.
У
нас имеется
пример
максимальной системы
![]() -мерных
векторов, состоящей из
-мерных
векторов, состоящей из
![]() векторов. Это значит: всякая
максимальная линейно независимая
система векторов n–
мерного
пространства состоит из n
векторов.
векторов. Это значит: всякая
максимальная линейно независимая
система векторов n–
мерного
пространства состоит из n
векторов.
Следующее определение вводит термин, фиксирующий полученный результат и отражающий логику движения к этому результату.
|
Определение: (6.4) |
Число векторов, входящих в любую максимальную линейно независимую подсистему данной системы векторов, называется рангом этой системы. |
Замечание: ещё раз вспомним, что принципиально важно (!) различать понятия:
–
![]() -мерное
векторное пространство:
бесконечное множество различных
векторов;
-мерное
векторное пространство:
бесконечное множество различных
векторов;
– система
![]() -мерных
векторов: чаще
состоит из
конечного числа векторов или является
подмножеством векторов
-мерных
векторов: чаще
состоит из
конечного числа векторов или является
подмножеством векторов
![]() -мерного
пространства.
-мерного
пространства.
Следствие –2 теоремы 6.2:
– пусть
имеем две системы
![]() -мерных
векторов:
-мерных
векторов:
![]() ,
,![]() ,
...,
,
...,![]() , (А)
, (А)
![]() ,
,![]() ,...,
,...,![]() , (B)
, (B)
не
обязательно линейно независимые, причем
ранг системы (А)
равен числу
![]() ,
а ранг системы (B)
– числу
,
а ранг системы (B)
– числу
![]() .
Если система (А)
линейно выражается через систему (B),
.
Если система (А)
линейно выражается через систему (B),
![]() ≤
≤
![]() .
.
– если в данной линейно зависимой системе векторов выделены две максимальные линейно независимые подсистемы, то эти подсистемы содержат равное число векторов.
Если
в
![]() –мерном
векторном пространстве
–мерном
векторном пространстве
![]() выделена максимальная
линейно независимая система векторов
выделена максимальная
линейно независимая система векторов
![]() ,
,![]() ,...,
,...,![]() ,
то, по аналогии с 3-мерным геометрическим
пространством, эту систему векторов
принять в качестве базы
(по-другому: базиса): любой вектор
пространства
,
то, по аналогии с 3-мерным геометрическим
пространством, эту систему векторов
принять в качестве базы
(по-другому: базиса): любой вектор
пространства
![]() может быть выражен через векторы
может быть выражен через векторы
![]() ,
,![]() ,...,
,...,![]() в виде линейной комбинации.
в виде линейной комбинации.
Нами
установлены важнейшие понятия линейной
алгебры. В аналитической геометрии в
3-мерном векторном пространстве мы имеем
вполне удобные средства для решения
задачи выделения из данной системы
векторов максимального числа линейно
независимых векторов (вспомним:
коллинеарность и компланарность
векторов). Для
![]() -мерных
векторов простого решения задачи
вычисления ранга системы векторов из
определения явно не просматривается.
Нужны какие-то дополнительные средства.
-мерных
векторов простого решения задачи
вычисления ранга системы векторов из
определения явно не просматривается.
Нужны какие-то дополнительные средства.
При изучении алгебры матриц мы рассматривали строки заданной матрицы как векторы, так же относились и к ее столбцам. Но тогда по отношению к строкам-векторам и столбцам-векторам можно отнести вопрос о ранге соответствующих систем векторов!
|
Определение: (6.5) |
Максимальное
число линейно независимых столбцов
матрицы A
(то
есть число столбцов, входящих в любую
подсистему линейно независимых
столбцов),
называется рангом
этой матрицы;
обозначение – |
Ранг матрицы можно было бы определить, используя систему ее строк–векторов. Оказывается (будет доказано!) ранг системы строк равен рангу системы столбцов матрицы. Поэтому будем говорить о ранге матрицы, не уточняя, учтена линейная независимость столбцов или строк.
Введем
понятие минора для прямоугольной (![]() ,
,![]() )
матрицы:
)
матрицы:
– выберем
в матрице
A
произвольные
![]() строк и
строк и
![]() столбцов;
столбцов;
– определитель
![]() -го
порядка,
составленный из элементов выделенных
строк и столбцов, называется минором
-го
порядка,
составленный из элементов выделенных
строк и столбцов, называется минором
![]() -го
порядка матрицы А.
-го
порядка матрицы А.
|
Теорема: (6.3) |
Если
все миноры
|
►Доказательство.
Это следует из теоремы Лапласа. Если
разложить минор порядка
![]() +
+![]() по любым его
по любым его
![]() строкам, то получим сумму произведений
миноров
строкам, то получим сумму произведений
миноров
![]() -го
порядка на их алгебраические дополнения
(соответственно). Так как все
миноры
-го
порядка на их алгебраические дополнения
(соответственно). Так как все
миноры
![]() -го
порядка равны нулю, то и минор порядка
-го
порядка равны нулю, то и минор порядка
![]() +
+![]() равен нулю. ◄
равен нулю. ◄
|
Теорема: (6.4) |
Наивысший
порядок отличных от
нуля миноров матрицы
A
порядка
( |
►Доказательство.
Пусть наивысший порядок отличных от
нуля миноров матрицы
A
равен
![]() .
Пусть такой минор D
порядка
.
Пусть такой минор D
порядка
![]() стоит в левом верхнем углу матрицы и
D≠0.
Учитывая свойства определителя, можем
утверждать, что первые
стоит в левом верхнем углу матрицы и
D≠0.
Учитывая свойства определителя, можем
утверждать, что первые
![]() столбцов и строк матрицы
A
линейно
независимы.
столбцов и строк матрицы
A
линейно
независимы.
Докажем,
что всякий столбец-![]() матрицы (
матрицы (![]() <
<![]() ≤
≤![]() )
будет линейной комбинацией первых
)
будет линейной комбинацией первых
![]() столбцов. Построим для выделенного
минора D
окаймляющий
минор
с элементами столбца-
столбцов. Построим для выделенного
минора D
окаймляющий
минор
с элементами столбца-![]() и строки-
и строки-![]() :
:
-
 =
=

…



D

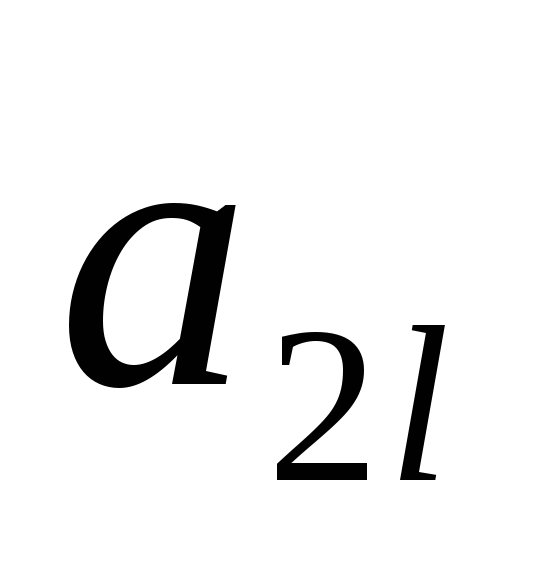
…
…
…


…



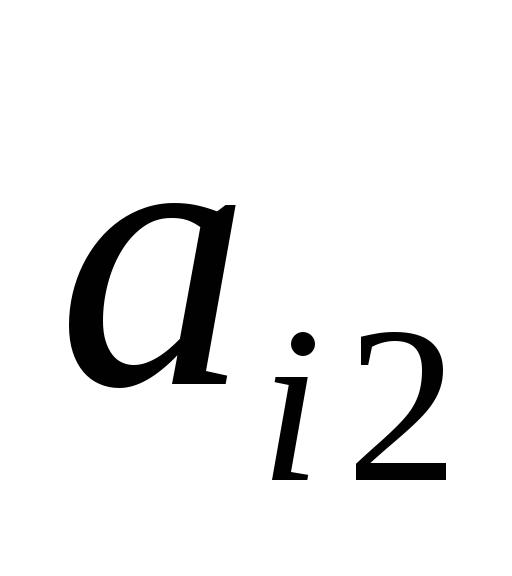
…


Определитель
![]() равен нулю при любом
равен нулю при любом
![]() :
:
– при
![]() >
>
![]() минор
минор
![]() имеет порядок (
имеет порядок (![]() +1),
и потому равен нулю (так выбран
+1),
и потому равен нулю (так выбран
![]() );
);
– при
![]() ≤
≤
![]() «минор»
«минор»
![]() имеет две равные строки (хотя фактически
не является минором матрицы А).
имеет две равные строки (хотя фактически
не является минором матрицы А).
Запишем
разложение минора
![]() по нижней его строке:
по нижней его строке:
![]() +
+![]() +…+
+…+![]() +
+![]() =0, (12)
=0, (12)
откуда (учитываем, что D ≠0) получаем равенство:
![]() =
=![]() –
–![]() –…–
–…–![]() , (13)
, (13)
которое
справедливо при всех
![]() =
1,
2,…,
s
, причем его коэффициенты
=
1,
2,…,
s
, причем его коэффициенты ![]() не зависят от значения
не зависят от значения
![]() .
Это значит, что весь столбец -
.
Это значит, что весь столбец -
![]() матрицы
A
является
суммой ее первых
матрицы
A
является
суммой ее первых
![]() столбцов, взятых с коэффициентами –
столбцов, взятых с коэффициентами –![]() ,
j
= 1,
2,…,
,
j
= 1,
2,…,
![]() .
.
Следовательно,
в системе столбцов матрицы
A
найдена
максимальная линейно независимая
подсистема, состоящая из r
столбцов. Это значит, что ранг матрицы
A равен
![]() .
◄
.
◄
Замечание:
доказательство теоремы не использует
равенство нулю всех
миноров (![]() +1)
порядка матрицы А,
а только те, которые окаймляют данный
не равный нулю минор
+1)
порядка матрицы А,
а только те, которые окаймляют данный
не равный нулю минор
![]() -
го порядка D.
-
го порядка D.
Получено правило вычисления ранга матрицы:
– при вычислении ранга матрицы переходят от миноров меньших порядков, к минорам больших порядков;
– если
уже найден минор
![]() -
го порядка не равный нулю, то следует
переходить к окаймлению
его минором (
-
го порядка не равный нулю, то следует
переходить к окаймлению
его минором (![]() +1)-го
порядка;
+1)-го
порядка;
– если
все окаймляющие миноры (![]() +1)-го
порядка равны нулю, то ранг матрицы
равен числу
+1)-го
порядка равны нулю, то ранг матрицы
равен числу
![]() .
.
|
Теорема: (6.5) |
Максимальное число линейно независимых строк всякой матрицы равно максимальному числу ее линейно независимых столбцов, то есть равно рангу этой матрицы. |
►Доказательство. Это следует из равноправия строк и столбцов в любом определителе-миноре! ◄
Следствие:
Определитель
![]() -го
порядка тогда и только тогда равен нулю,
если между его строками существует
линейная зависимость.
-го
порядка тогда и только тогда равен нулю,
если между его строками существует
линейная зависимость.
►Доказательство.
В одну сторону это было доказано при
доказательстве свойств определителей
n-го
порядка. Пусть известно, что определитель
![]() -го
порядка равен нулю. Но тогда соответствующая
матрица
-го
порядка равен нулю. Но тогда соответствующая
матрица
![]() -го
порядка, единственный минор
-го
порядка, единственный минор
![]() -го
порядка которой равен нулю, имеет ранг:
-го
порядка которой равен нулю, имеет ранг:
![]() <
<![]() .
Последнее значит, что строки матрицы
линейно зависимы. То же можно сказать
о столбцах. ◄
.
Последнее значит, что строки матрицы
линейно зависимы. То же можно сказать
о столбцах. ◄
Кроме правила окаймляющих миноров применяют еще правило приведения матрицы к диагональному виду путем элементарных преобразований (не меняют ранга!):
– транспозиция двух строк или столбцов;
– умножение строки (столбца) на число, не равное нулю;
– прибавление к строке (столбцу) другой строки (столбца), умноженной на некоторое число;
– после получения диагональной формы матрицы число единиц на главной диагонали определяет ранг матрицы.
Замечания: 1) правило приведения матрицы к диагональному виду применяют обычно в тех случаях, когда требуется только определить ранг матрицы: следить за всеми перестановками строк и столбцов неудобно;
2) если столбцы не переставлять (за одними строками следить не так сложно!), а единицы на главной диагонали получать способом уравнивания коэффициентов, то метод вполне удобен для выделения в системе векторов-строк максимальной линейно независимой подсистемы векторов.
|
Определение: (6.6) |
Пусть ранг матрицы A равен –r. Любой, отличный от нуля минор матрицы A порядка r, называют базисным. |
Приведённые ниже примеры иллюстрируют все рассмотренные вопросы теории и способы вычисления ранга системы векторов, ранга матрицы, построения векторов в заданном базисе.
☺☺
Пример 6-05: Для
векторов:
![]() =(4,1,3,-2),
=(4,1,3,-2),
![]() =(1,2,-3,2),
=(1,2,-3,2),
![]() =(16,9,1,-3)
найти
линейную комбинацию:
3
=(16,9,1,-3)
найти
линейную комбинацию:
3![]() +5
+5![]() –
–![]() =
=![]() .
.
Решение:
Используя
определение суммы (и разности) векторов
и умножение вектора на число,
запишем: ![]() =3(4,1,3,-2)+5(1,2,-3,2)–(16,9,1,-3)=(12,3,9,-6)+(5,10,-15,10)
–(16,9,1,-3)=(1,4,-7,7)
=3(4,1,3,-2)+5(1,2,-3,2)–(16,9,1,-3)=(12,3,9,-6)+(5,10,-15,10)
–(16,9,1,-3)=(1,4,-7,7)
Ответ:
![]() =(1,4,-7,7).
=(1,4,-7,7).
Пример
6-06:Найти
ранг ![]() матрицы: A=
матрицы: A= методом окаймляющих миноров.
методом окаймляющих миноров.
Решение:
1). Так как в матрице
есть элементы не равные нулю, то ранг
матрицы
![]() .
Окаймление любого из них приводит к
минору 2-го порядка.
.
Окаймление любого из них приводит к
минору 2-го порядка.![]()
2). Не равных нулю
миноров 2-го порядка несколько. Это
значит, что
![]() .
Выделим для окаймления минор (не равен
нулю), расположенный в правом верхнем
углу:
.
Выделим для окаймления минор (не равен
нулю), расположенный в правом верхнем
углу:
-
2
-1
3
-2
4
4
-2
5
1
7
1
2
-1
1
8
2
3
2
1
3). Окаймляющие
миноры будем обозначать:
![]() ,
где
,
где![]() –
указывает номер отмеченной для окаймления
строки,
–
указывает номер отмеченной для окаймления
строки,![]() –
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
–
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
![]() =
= =3
=3![]() –5
–5![]() +1
+1![]() =m1·(–54)–h1·(–36)+g1·(–18)=3·(–54)–5·(–36)+1·(–18)
=0;
=m1·(–54)–h1·(–36)+g1·(–18)=3·(–54)–5·(–36)+1·(–18)
=0;
Замечание:
параметры: m1,
h1,
g1
изменяются при переходе к минорам
![]() ,
,![]() ,
числа:(–54),
(–36),
(–18)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
,
числа:(–54),
(–36),
(–18)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
![]() =
= =
m2·(–54)–h2·(–36)+g2·(–18)=(–1)·(–54)
–(–2)·(–36)+(–1)·(–18)
=0;
=
m2·(–54)–h2·(–36)+g2·(–18)=(–1)·(–54)
–(–2)·(–36)+(–1)·(–18)
=0;
![]() =
= =
m3·(–54)–h3·(–36)+g3·(–18)=2·(–54)
–4·(–36)+2·(–18)
=0.
=
m3·(–54)–h3·(–36)+g3·(–18)=2·(–54)
–4·(–36)+2·(–18)
=0.
4).
Так как все миноры 3-го порядка оказались
равными нулю, то ранг
![]() матрицыA
равен 2.
матрицыA
равен 2.
Ответ:![]() =
2.
=
2.
Пример
6-07:Найти
ранг матрицы:
 методом окаймляющих миноров.
методом окаймляющих миноров.
Решение:
1). Так как в матрице
есть элементы не равные нулю, то ранг
матрицы
![]() .
Окаймление любого из них приводит к
минору 2-го порядка.
.
Окаймление любого из них приводит к
минору 2-го порядка.
2). Не равных нулю
миноров 2-го порядка несколько. Это
значит, что
![]() .
Выделим для окаймления минор (не равен
нулю), расположенный в левом верхнем
углу:
.
Выделим для окаймления минор (не равен
нулю), расположенный в левом верхнем
углу:
-
1
3
5
-1
2
-1
-3
4
1
5
1
-1
7
2
7
7
9
1
1
2
3). Окаймляющие
миноры будем обозначать:
![]() ,
где
,
где![]() –
указывает номер отмеченной для окаймления
строки,
–
указывает номер отмеченной для окаймления
строки,![]() –
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
–
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
![]() =
= =5
=5![]() –(–3)
–(–3)![]() +(–1)
+(–1)![]() =m1·(7)–h1·(–14)+g1·(–7)=5·(7)–(–3)·(–14)+(–1)·(–7)=0;
=m1·(7)–h1·(–14)+g1·(–7)=5·(7)–(–3)·(–14)+(–1)·(–7)=0;
Замечание:
параметры: m1,
h1,
g1
изменяются при переходе к минору
![]() ,
числа:(7),
(–14),
(–7)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
,
числа:(7),
(–14),
(–7)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
![]() =
= =
m2·(7)–h2·(–14)+g2·(–7)=
(–1)·(7)–4·(–14)+7·(–7)=0;
=
m2·(7)–h2·(–14)+g2·(–7)=
(–1)·(7)–4·(–14)+7·(–7)=0;
![]() =
= =5
=5![]() –(–3)
–(–3)![]() +9
+9![]() =m1·(21)–h1·(–14)+g1·(–7)=5·(21)–(–3)·(–14)+9·(–7)=0;
=m1·(21)–h1·(–14)+g1·(–7)=5·(21)–(–3)·(–14)+9·(–7)=0;
Замечание:
параметры: m1,
h1,
g1
изменяются при переходе к минору ![]() ,
числа: (21),
(–14),
(–7)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
,
числа: (21),
(–14),
(–7)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
![]() =
= =
m2·(21)–h2·(–14)+g2·(–7)=
(–1)·(21) –4·(–14)+1·(–7)
≠0.
=
m2·(21)–h2·(–14)+g2·(–7)=
(–1)·(21) –4·(–14)+1·(–7)
≠0.
4).
Так как нашёлся минор 3-го порядка не
равный нулю, то ранг
![]() .
Вычислим определитель:
.
Вычислим определитель:
![]() =
= =(1)=2·
=(1)=2· =(2)=2·
=(2)=2·
Операции:
(1):
[C1]–[C2];
[C3]–[C2];
выносим общий множитель число 2 из [C3].
(2):
[R3]–[R2];
[R2]+[R1];
в определителе обнаружено: [R2]=[R3]
→ ![]() =0.
=0.
4).
Следует:
![]() .
.
Ответ:![]() =
3.
=
3.
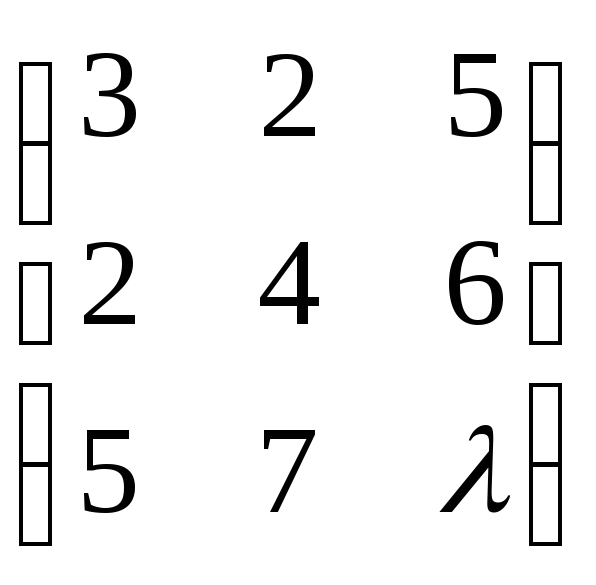
Пример
6-08:Чему
равен ранг матрицы:
 при различных значениях
при различных значениях![]() ?
?
Решение:
1). Выделим для окаймления минор 2-го порядка (не равен нулю), расположенный в левом нижнем углу:
-
1
1
λ
-1
2
2
-1
λ
5
1
10
-6
λ
1
2
2). Вычислим
окаймляющие миноры
![]() и
и![]() :
:
![]() =
= =
= =
=![]() >
0 при любом
>
0 при любом![]() .
.
3). Итак, выделен
минор 3-го порядка, не равный нулю при
любом
![]() .
Так как миноров большего порядка нет,
то
.
Так как миноров большего порядка нет,
то![]() =
3.
=
3.
Ответ:
![]() =
3 при любом
=
3 при любом![]() .
.
Пример 6-09:Элементарными преобразованиями матрицы называют следующие преобразования:
1)умножение строки или столбца на число, отличное от нуля;
2)прибавление к одной строке (столбцу) другой строки (столбца), умноженной на любое число;
3)перестановка двух строк (столбцов).
Доказать, что элементарные преобразования не меняют рангаматрицы.
Решение:
1). В соответствии с теоремой 6.4 ранг матрицы оценивается минорами матрицы, точнее: фактами равенства и неравенства нулю миноров, то есть определителей.
2). Так как элементарные преобразования не могут превратить определитель не равный нулю в определитель равный нулю, и наоборот, то названные преобразования не могут изменить ранга матрицы.
Замечание: Можно было бы воспользоваться теоремой о равенстве рангов двух эквивалентных систем векторов: названные преобразования переводят заданную систему векторов (строки матрицы или столбцы) в эквивалентную систему векторов!
Ответ:доказано.
Пример
6-10:Найти
ранг матрицы: ![]() =
= при помощи элементарных преобразований.
при помощи элементарных преобразований.
Решение:
1). Преобразуем матрицу при помощи элементарных преобразований.
![]() =(1)→
=(1)→ =(2)→
=(2)→ =(3)→
=(3)→
Операции: (1): [C4]+[C2]·3; [C5]–[C1]·3; [C1]–[C5]·4. (2): [C3]+[C1]·4; [R1]+[R3]; [R2]+[R3]; при помощи 1 обнуляем элементы [R4]. (3): [C5]+[C1]; [C2]–[C1]·55; делим [C1] на (-3). Завершение очевидно:
 ,
или
,
или
 .
.
2). Видим: ранг матрицы равен 2.
Ответ:![]() =
2.
=
2.
Пример
6-11:Для
матриц ![]() и
и ![]() одинаковой размерности построили
матрицу
одинаковой размерности построили
матрицу ![]() .
Доказать, что ранг суммы двух матриц не
больше суммы их рангов.
.
Доказать, что ранг суммы двух матриц не
больше суммы их рангов.
Решение:
1). Понятие суммы
матриц использовано, чтобы подсказать,
что используются векторы одного
векторного пространства![]() .
Тогда матрицу
.
Тогда матрицу![]() можно рассматривать как подпространство
можно рассматривать как подпространство![]() ,
а матрицу
,
а матрицу![]() как подпространство
как подпространство![]() .
.
2). В таком случае
задачу можно понимать так: объединяется
два подпространства векторов некоторого
векторного пространства
![]() ,
причём ранг одного
,
причём ранг одного![]() ,
второго
,
второго![]() .
Требуется оценить ранг суммы подпространств.
.
Требуется оценить ранг суммы подпространств.
3). Но, тогда оценка
ранга системы векторов
![]() очевидна:
очевидна:![]() .
.
Ответ: доказано:
![]() .
.
Пример
6-12:Выяснить,
является ли система векторов:  линейно зависима или линейно независима.
линейно зависима или линейно независима.
Решение:
1). Запишем систему
векторов в виде матрицы и применим к
ней любой из способов вычисления ранга:
![]() =
= .
.
2). Преобразуем матрицу при помощи элементарных преобразований.
![]() =(1)→
=(1)→
 =(2)→
=(2)→
 =(3)→
=(3)→

Операции: (1): [C2]+[C1]; [C4]–[C1]; [C1]–[C4]·2. (2): [R4]+[R1]·3; [R3]+[R1]·3; [C4]–[C2]; при помощи 1 обнуляем элементы [C3]. (3): [C1]·(–1); [C3] делим на 6, [C4] на (-3), после чего [R4]–[R3].
3). Видим: ранг матрицы равен 3. Это значит, что система векторов зависима.
Замечание:
эту задачу можно решить вычислением
определителя ![]() :
если определитель равен нулю, то система
зависима, если не равен нулю, то система
независима!
:
если определитель равен нулю, то система
зависима, если не равен нулю, то система
независима!
Ответ:![]() =3,
система векторов зависима.
=3,
система векторов зависима.
Пример
6-13: Пусть имеем: Найти все значения
Найти все значения
![]() ,
при которыхвектор
,
при которыхвектор
![]() линейно выражается через векторы:
линейно выражается через векторы:![]() ,
,![]() ,
,![]() .
.
Решение:
1). Вектор
![]() линейно выражается через векторы:
линейно выражается через векторы:![]() ,
,![]() ,
,![]() ,
если эти векторы независимы.
,
если эти векторы независимы.
2). Из векторов
![]() ,
,![]() ,
,![]() составим матрицу:
составим матрицу:![]() =
= и
вычислим её определитель:
и
вычислим её определитель:
![]() =
= =(1)=
=(1)= =(2)=(–1)·
=(2)=(–1)·![]() ·8·
·8·![]() =8
=8![]() .
.
Операции: (1): [C2]–[C1]; [R3]–[R2]; [R2]+[R1]·2. (2): вычисляем определитель разложением по столбцу-2.
3). Видим: ранг
матрицы равен 3, если
![]() .
Это и требуется для линейной независимости
системы векторов:
.
Это и требуется для линейной независимости
системы векторов:![]() ,
,![]() ,
,![]() .
.
Ответ:![]() .
.
Пример
6-14:Найти
все базы системы векторов:
Решение:
1). В
системевекторов:![]() ,
,![]() ,
,![]() легко обнаруживается зависимость:
легко обнаруживается зависимость:![]() .
Вектор не выражается через векторы
.
Вектор не выражается через векторы![]() ,
,![]() ,
,![]() .
.
2). Это значит, что
базой могут служить пары векторов:
(![]() ,
,![]() );
(
);
(![]() ,
,![]() );
(
);
(![]() ,
,![]() ).
).
Ответ:все базы системы: (![]() ,
,![]() );
(
);
(![]() ,
,![]() );
(
);
(![]() ,
,![]() ).
).
Пример
6-15: Имеемсистему
векторов: Найти какую-нибудь
базу этой системы векторов и все векторы
системы, не входящие в эту базу, выразить
через векторы базы.
Найти какую-нибудь
базу этой системы векторов и все векторы
системы, не входящие в эту базу, выразить
через векторы базы.
Решение:
1). Для заданной системы векторов составим матрицу и выделим базовый минор. Выделим для окаймления минор, не равен нулю, расположенный в левом верхнем углу:
-
1
2
3
-4
2
3
-4
1
1
2
-5
8
-3
2
5
26
-9
-12
3
3
-4
1
2
1
2
2). Окаймляющие
миноры будем обозначать:
![]() ,
где
,
где![]() –
указывает номер отмеченной для окаймления
строки,
–
указывает номер отмеченной для окаймления
строки,![]() –
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
–
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
![]() =
= =3
=3![]() –(–4)
–(–4)![]() +8
+8![]() =m1·(–16)–h1·(–9)+g1·(–1)=3·(–16)–(–4)·(–9)+8·(–1)
=m1·(–16)–h1·(–9)+g1·(–1)=3·(–16)–(–4)·(–9)+8·(–1)![]() 0;
0;
3). Выделим для
окаймления минор
![]() 0:
0:
-
1
2
3
-4
2
3
-4
1
2
-5
8
-3
1
5
26
-9
-12
2
3
-4
1
2
1
4).Окаймляющие миноры
![]() и
и![]() – определители 4-го порядка. Так как
указанные миноры отличаются только
строкой-4, то их вычисление рационально
провести разложением по строке-4. Это
позволит применить единый шаблон
вычислений!
– определители 4-го порядка. Так как
указанные миноры отличаются только
строкой-4, то их вычисление рационально
провести разложением по строке-4. Это
позволит применить единый шаблон
вычислений!
![]() =
= =5·
=5· –26·
–26·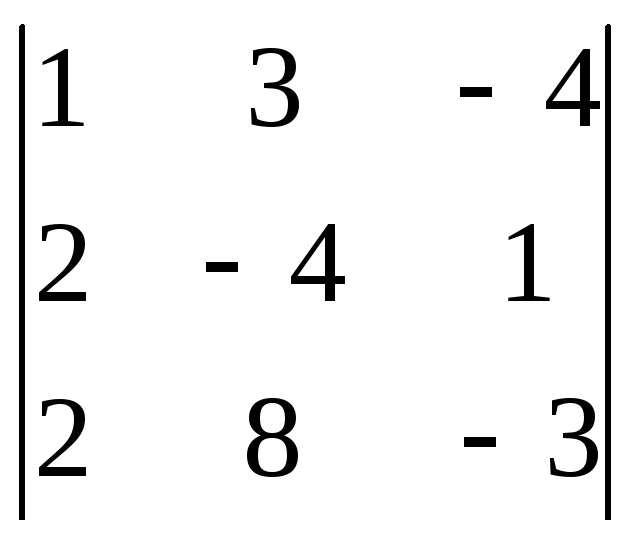 +(–9)·
+(–9)· –(–12)·
–(–12)· ,
,
или:
![]() =
m1·(4)–h1·(–68)+g1·(76)
–q1·(–92)=5·4–26·(–68)+(–9)·76
–(–12)·
(–92)=0;
=
m1·(4)–h1·(–68)+g1·(76)
–q1·(–92)=5·4–26·(–68)+(–9)·76
–(–12)·
(–92)=0;
Замечание:
параметры: m1,
h1,
g1,
q1
изменяются при переходе к минору ![]() ,
числа: (4),
(–68),
(76),
(–92)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
,
числа: (4),
(–68),
(76),
(–92)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
![]() =
= =
m2·(4)–h2·(–68)+g2·(76)
–q2·(–92)=
3·4–(–4)·(–68)+1·76
–2·
(–92)=0.
=
m2·(4)–h2·(–68)+g2·(76)
–q2·(–92)=
3·4–(–4)·(–68)+1·76
–2·
(–92)=0.
5).
Векторы:
![]() ,
,![]() ,
,![]() можно использовать как базу. Запишем
для векторов
можно использовать как базу. Запишем
для векторов![]() ,
,![]() линейные комбинации векторов
линейные комбинации векторов![]() ,
,![]() ,
,![]() :
:
![]() =
=
![]() +
+![]() +
+![]() =
=![]() ·(1,2,3,-4)+
·(1,2,3,-4)+![]() ·(2,3,-4,1)+
·(2,3,-4,1)+![]() ·(2,-5,8,-3)=(5,26,-9,-12),
·(2,-5,8,-3)=(5,26,-9,-12),
![]() =
=![]() +
+![]() +
+![]() =
=![]() ·(1,2,3,-4)+
·(1,2,3,-4)+![]() ·(2,3,-4,1)+
·(2,3,-4,1)+![]() ·(2,-5,8,-3)=(3,-4,1,2),
·(2,-5,8,-3)=(3,-4,1,2),
где величины:
![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() подлежат вычислению из систем уравнений:
подлежат вычислению из систем уравнений:
 и
и
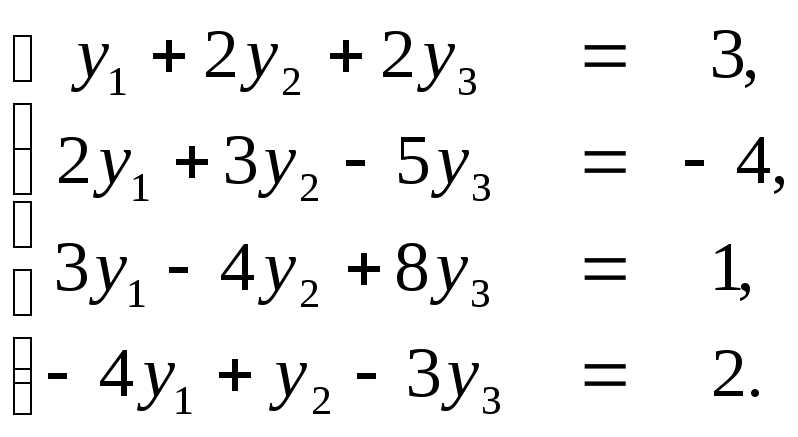
Так
как определители 4-го порядка:
![]() =
= =0
и
=0
и ![]() =
= =0,
то уравнения зависимы. В то же время
определитель 3-го порядка:
=0,
то уравнения зависимы. В то же время
определитель 3-го порядка:
![]() =
=
![]() 0.
Это значит, что первые три уравнения
системы независимы и эквивалентны всей
системе. Их и решаем:
0.
Это значит, что первые три уравнения
системы независимы и эквивалентны всей
системе. Их и решаем:
 и
и

откуда
вычисляем (любым способом!): ![]() =5,
=5,![]() =2,
=2,![]() =–2;
=–2;![]() =–1,
=–1,![]() =1,
=1,![]() =1;
=1;
6).
Результат: если база –
векторы ![]() ,
,![]() ,
,![]() ,
то
,
то![]() =5
=5![]() +2
+2![]() –2
–2![]() ;
;
![]() =–
=–![]() +
+![]() +
+![]() .
.
Ответ:если база –
векторы ![]() ,
,![]() ,
,![]() ,
то
,
то![]() =5
=5![]() +2
+2![]() –2
–2![]() ;
;
![]() =–
=–![]() +
+![]() +
+![]() ..
..
Набор поясняющих Примеров иллюстрирует наиболее сложные теоретические вопросы и предлагает рациональные схемы вычислений участвующих величин. После приобретения определённых устойчивых навыков, каждый может отработать свои алгоритмы решения и вычислений конкретных алгебраических выражений.
☻
