§ 7. Пары форм.

Пусть имеем пару квадратичных форм: и . Существует ли линейное преобразование неизвестных: =, которое обе формы, одновременно, приводит к каноническому виду? В общем случае ответ отрицательный!

Если одна из квадратичных форм положительно определенная, то имеет место теорема:

Теорема: (11.6.1)

Пусть и – пара квадратичных форм, причем форма положительно определенная. Существует невырожденное линейное преобразование, одновременно приводящее обе формы к каноническому виду.

►Пусть линейное преобразование переменных: = привело квадратичную форму g к виду:

=++…+, (1)

при этом квадратичная форма приобрела вид, в общем случае не канонический вид, от новых неизвестных :

=. (2)

Теперь совершим ортогональное преобразование переменных: =, причём такое, что форма приводится к главным осям, а в форме сохранилась сумма квадратов переменных: по определению ортогонального преобразования:

==++…+,

=++…+= ++…+.

Искомое линейное преобразование: =. ◄

☺☺

Пример 12–17: Задана пара квадратичных форм: =и =. Выяснить, что одна из них положительно определённая. Найти невырожденное линейное преобразование, приводящее положительно определённую форму к нормальному виду, а другую форму пары к каноническому виду. Учесть, что линейное преобразование определяется неоднозначно.

Решение:

1). Запишем матрицы заданных квадратичных форм: = и =. Применяя критерий Сильвестра, легко заметить, что положительно определённой формой является форма .

2). Приведём форму к нормальному виду. Так как в записи формы естьневыделенные квадратыпеременных, то применим преобразованиеR¹. Изобразим наши действия при помощи таблицы, выделяя основные штрихи наблюдений:

													Замена:
	1	-1		=						1	-1		=–, =.						1	-1
	-1									-1	4								0	1

*Левый рисунок матрицы показывает, что имеетсяневыделенный квадрат переменной при наличии в записи слагаемого и слагаемого: , куда переменная входит сомножителем. Всё это сигналит:нужно применять преобразование R¹. Средний рисунок матрицы показывает, что мы наметили в записи формывыделить квадрат переменной , причём так, чтобы переменная не использовалась, как сомножитель в других слагаемых этой формы. Таблица замены показывает необходимое преобразование переменных: видим, как используются коэффициенты первой строки матрицы среднего рисунка. Матрица отражает преобразование переменных:=·, или=·. (1.1)

Для замены в форме (1.1) переменной на переменную из преобразования (1.1) легко получить обратное преобразование:

=·, или =·. (1.2)

Подставляя выражения , в исходную запись формы , в результате невырожденного линейного преобразования переменных получим новое выражение формы , в которой выделен квадрат неизвестной :

=. (1.3)

3). Если применим преобразование: =,=·, то квадратичная форма примет вид:

=. (1.4)

4). Воспользуемся цепочкой преобразований переменных величин:

==–,==→=+, =. (1.5)

5). Применяя линейное преобразование (1.5) к квадратичной форме , получим:

=. (1.6)

6). Теперь необходимо привести форму к главным осям. Это значит, необходимо найти характеристические корни матрицы квадратичной формы:

= → ==0 → =–2, =. (1.7)

Это значит, что матрица квадратичной формы принимает вид:=, а квадратичная форма может быть записана в виде:=– канонический вид формы.

7). Остаётся найти ортогональное линейное преобразование, которое привело квадратичную форму к каноническому виду, оставляя запись формы в нормальном виде:

Записываем систему уравнений для нахождения собственных векторов линейного преобразования, соответствующим найденным собственным значениям: (A)

Для собственного значения =–2 система (A) принимает вид:: 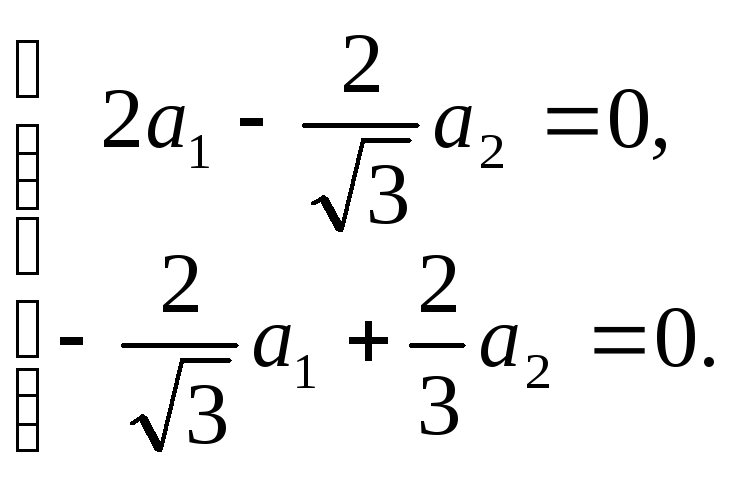(B)

Так как определитель системы равен нулю, то независимо одно уравнение. Пусть =1, тогда вычислим: =. Собственный вектор для собственного значения: =(1, ).

Для собственного значения = система (A) принимает вид:: (C)

Так как определитель системы равен нулю, то независимо одно уравнение. Пусть =–, тогда вычислим: =1. Собственный вектор для собственного значения: =(–,1).

Легко заметить, что векторы и ортогональны. Остаётся нормировать собственные векторы: =, =. Это значит, что форма: = была приведена к каноническому виду: = ортогональным преобразованием:

=,=,

=→=, (1.8)

Учитывая линейное преобразование (1.5) и ортогональное преобразование (1.8), запишем общее линейное преобразование, преобразующее форму к нормальному виду, а форму к каноническому виду: =, =. (1.9)

Ответ: квадратичные формы: = – нормальный вид, = – канонический вид. Ортогональное преобразование переменных: =·.

☻

Замечание: решение задачи приведения пары форм к простейшей записи, даже для достаточно компактной пары, использует многошаговый алгоритм, трудоёмкий в вычислениях; для практического использования названного алгоритма целесообразно построить стандартный алгоритм решения задачи для общего случая нескольких переменных формы: ,,,...,.

Общий алгоритм приведения пары квадратичных форм к простейшему виду.

A¹: Пусть имеется пара квадратичных форм, одна из которых – положительно определённая: обычно не сообщается, какая именно. Требуется привести положительно определённую форму к нормальному виду, а другую – к каноническому виду.

A²: Применяя критерий Сильвестра выделяем положительно определённую форму. Пусть это будет форма .

A³: Приводим форму к нормальному виду. Определяем линейное преобразование переменных, приводящее форму к нормальному виду:=·.

A⁴: Применяем линейное преобразование переменных:=·к квадратичной форме:f. В общем случае эта форма не принимает канонический вид.

A⁵: Приводим квадратичную форму:fк главным осям. Для этого находим собственные значения и собственные векторы для характеристической матрицы квадратичной формыf, выраженной через переменные. Базис, составленный из собственных векторов, превращаем в ортонормированный базис. Координаты векторов этого базиса определяют ортогональное преобразование переменных, а именно:=·.

A⁶: Остаётся записать линейное преобразование:=·и оформить ответ решённой задачи!

Набор поясняющих примеров иллюстрирует наиболее сложные теоретические вопросы и предлагает рациональные схемы вычислений участвующих величин.