§ 6. Приведение квадратичной формы к главным осям.

При рассмотрении линейных преобразований евклидова пространства мы познакомились с двумя специальными преобразованиями: симметрическим и ортогональным. Совместное их использование приводит к следующей теореме.

Теорема: (11.11)

Пусть в евклидовом пространстве симметрическое преобразование задано симметрической матрицей . Найдется ортогональное преобразование , определяемое ортогональной матрицей , которое приводит матрицу преобразования к диагональному виду. Эта матрица: =.

►Пусть имеем симметрическую матрицу порядка . Пусть в евклидовом пространстве задан ортонормированный базис =. Матрица определяет в базисе симметрическое преобразование . Согласно Теореме 10.9 в пространстве для любого симметрического преобразования всегда существует ортонормированный базис, составленный из собственных векторов этого преобразования: =. Пусть матрица перехода от базиса к базису – матрица , причём и – матрицы-столбцы. Это значит: =·. Известно, что матрица линейного преобразования при переходе к новому базису подобна матрице , то есть: =. ◄

Следствие: всякая действительная квадратичная форма некоторым ортогональным преобразованием может быть приведена к каноническому виду.

►Воспользуемся Теоремой 11.11: симметрическая матрица ортогональным преобразованием приводится к матрице диагонального вида: =. Перепишем последнее равенство в виде: =.

Так как матрица ортогональна, то, согласно Теореме 11.6: =. Тогда =. Но именно так преобразуется симметрическая матрица квадратичной формы преобразованием переменных: =. Действительно: f ===. ◄

Замечание: может существовать много различных ортогональных преобразований неизвестных, приводящих данную квадратичную форму к каноническому виду: неоднозначность заложена в неоднозначности построения собственных векторов и их ортогонализации!

Хотя выбор ортогональных преобразований, приводящих квадратичную форму к каноническому виду, определяется неоднозначно, сам этот канонический вид определяется однозначно. Это устанавливает следующая теорема.

Теорема: (11.12)

Каково бы ни было ортогональное преобразование , приводящее к каноническому виду квадратичную форму с матрицей , коэффициентами канонической записи будут характеристические корни матрицы , взятые с их кратностями.

►Пусть некоторым ортогональным преобразованием квадратичная форма приведена к каноническому виду:

f =++…+.

Если представить, что исходная запись квадратичной формы была представлена выражением:

–(++…+). (1)

Легко заметить, что матрицей квадратичной формы (1) является матрица . К форме (1) применим ортогональное преобразование, которое, как известно, оставляет инвариантной сумму квадратов неизвестных, причём такое, что получим запись квадратичной формы в виде:

++…+–(++…+). (2)

Квадратичной форме (1) соответствует определитель: , а квадратичной форме (2) – определитель: =…. (3)

Учитывая, что матрицы квадратичных форм (1) и (2), связаны равенством: =, а также равенство для определителей: ==·=, получаем равенство:

=…, (4)

из равенства (4) вытекает утверждение теоремы. ◄

Учитывая доказанные теоремы и следствия, можем определить общий алгоритм приведения квадратичной формы к каноническому виду.

Алгоритм приведения квадратичной формы к каноническому виду:

1) Для заданной симметрической матрицы квадратичной формы находим характеристические корни, то есть характеристические корни соответствующего линейного ортогонального преобразования .

2) С учётом кратности характеристических корней строим диагональную матрицу преобразованной квадратичной формы, а значит, и каноническую запись этой формы.

3) Находим собственные векторы симметрического преобразования. После ортогонализации и нормирования совокупности собственных векторов получаем базис . Связь исходного базиса с базисом определяется выражением: ==·.

4) Используя матрицу , можем записать выражение новых переменных квадратичной формы через старые переменные : =. Ясно, что одновременно: =

Используя представленный алгоритм, решим несколько примеров преобразования произвольной квадратичной формы к каноническому виду.

☺☺

Пример 12–13: Задана квадратичная форма:=. Найти её канонический вид, применяя ортогональное преобразование. Само преобразование не находить.

Решение:

1). Матрица квадратичной формы имеет вид: =– симметрическая. Составим её характеристический многочлен и найдём его корни:

==0 → ==4, =–2.

2) Характеристические корни ортогонального преобразования определяют матрицу этого преобразования в ортонормированном базисе: =.

3). Запишем квадратичную форму в каноническом виде:=.

Ответ: квадратичная формав каноническом виде:=.

Пример 12–14: Задана квадратичная форма: =. При­вести квадратичную форму к главным осям и определить соответствующее ортогональное преобразование.

Решение:

1). Составляем матрицу квадратичной формы: =.

2). Составляем характеристический многочлен: ==.

3). Используя характеристические корни, с учётом кратности, запишем квадратичную форму в каноническом виде: =.

4). Записываем систему уравнений для нахождения собственных векторов линейного преобразования, соответствующим найденным собственным значениям: (10.1)

5). Для собственного значения =1 система (10.1) принимает вид:

(10.2)

Легко заметить, что ранг системы (10.2) равен 1, то есть независимо только одно уравнение. Объявляя свободными неизвестными: ,,, получаем три независимых решения:

=(1, 1, 0, 0), =(1, 0, 1, 0), =(-1, 0, 0, 1). (10.3)

Применяя стандартный процесс ортогонализации векторов: ,,, получим систему попарно ортогональных векторов:

=(1, 1, 0, 0), =(, -, 1, 0), =(-, , , 1). (10.4)

6). Для собственного значения =–3 система (10.1) принимает вид:

(10.5)

Легко заметить, что ранг системы (10.5) равен 3, то есть независимы три уравнения. Объявляя свободной неизвестной: , получаем одно независимое решение:

=(-1, -1, -1, 1), (10.6)

Легко убедиться, что вектор ортогонален системе векторов: ,, .

7). Остаётся провести нормирование системы векторов ,, ,:

=, =, (10.7)

=, =.

8). Это значит, что заданная квадратичная форма приводится к главным осям ортогональным линейным преобразованием: =,

=, (10.8)

=.

=.

Ответ: квадратичная форма, приведённая к главным осям: =. Ортогональное преобразование переменных формы представлено (10.8).

Пример 12–15: Задана квадратичная форма: =. При­вести квадратичную форму к главным осям и определить соответствующее ортогональное преобразование.

Решение:

1). Матрица квадратичной формы имеет вид: =. Составим её характеристический многочлен и найдём его корни:

==0 → =3,=6, =9.

2). Запишем квадратичную форму в каноническом виде:=.

3). Остаётся найти ортогональное линейное преобразование, которое привело квадратичную форму к каноническому виду.

Записываем систему уравнений для нахождения собственных векторов линейного преобразования, соответствующих найденным собственным значениям: (A)

Для значения =3 система (A) принимает вид: (B)

Легко заметить, что независимы два уравнения. Пусть =–1, =2 → =2 → собственный вектор для собственного значения: =(2,2,–1).

Для значения =6 система (A) принимает вид: (С)

Легко заметить, что независимы два уравнения. Пусть =–1, =2 → =2 → собственный вектор для собственного значения: =(–1,2,2).

Для значения =9 система (A) принимает вид: (D)

Легко заметить, что независимы два уравнения. Пусть =–1, =2 → =2 → собственный вектор для собственного значения: =(2,–1,2).

Собственные векторы ,, независимы и ортогональны. После нормирования получим:

=(2,2,–1), =(–1,2,2), =(2,–1,2).

Это значит, что форма: = была приведена к каноническому виду: = ортогональным преобразованием:

=,=,=,

Ответ: квадратичная форма: = – канонический вид. Ортогональное преобразование: =··.

Пример 12–16: Задана квадратичная форма: =. При­вести квадратичную форму к главным осям и определить соответствующее ортогональное преобразование.

Решение:

1). Матрица квадратичной формы имеет вид: =. Составим её характеристический многочлен и найдём его корни:

==0 → =9, ==18.

2). Запишем квадратичную форму в каноническом виде:=.

3). Остаётся найти ортогональное линейное преобразование, которое привело квадратичную форму к каноническому виду.

Записываем систему уравнений для нахождения собственных векторов линейного преобразования, соответствующих найденным собственным значениям: (A)

Для значения =9 система (A) имеет вид:  , (B)

Легко заметить, что независимы два уравнения. Пусть =1, =2 → =2 → собственный вектор для собственного значения: =(1,2,2).

Для значения =18 система (A) имеет вид:  =. (С)

Легко заметить, что независимо одно уравнение. Пусть свободные неизвестные: и . Построим ФСР этой системы уравнений:

	a1	a2	a3
b2	-2	1	0
b3	-2	0	1

Собственные векторы ,, независимы, но не ортогональны. После применения процесса ортогонализации и нормирования получим:

=(1,2,2), = (–2,1,0), = (2,4,–5).

Это значит, что форма: = была приведена к каноническому виду: = ортогональным преобразованием:

=,=,=,

Ответ: квадратичная форма: = – канонический вид. Ортогональное преобразование: =·.

☻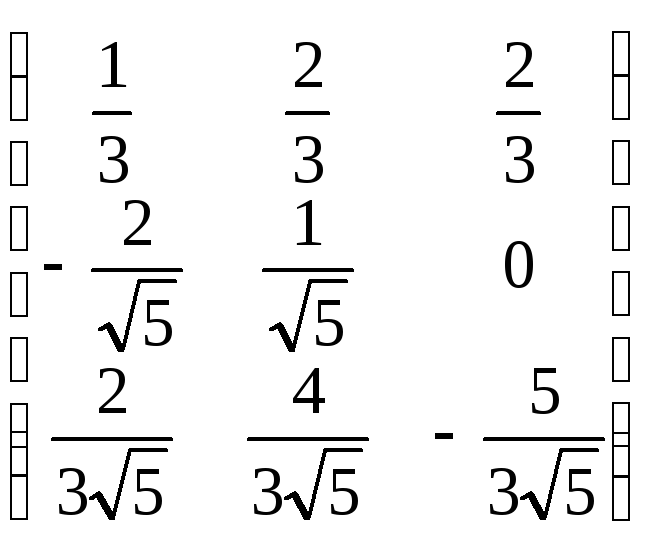