§ 7. Обобщающие примеры по теме: «Плоскость и прямая в пространстве».

Набор обобщающих Примеров соответствует требованиям «Семестрового плана» при изучении темы: «Плоскость и прямая в пространстве». Эти Примеры предназначены закрепить навыки применения общих алгоритмов решений, установленных в поясняющих Примерах.

☺ ☻ ☺

Пример 1–914: Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор= (5, 0,–3).

Решение:

1). Задача является простейшей при построении общего уравнения плоскости. Так как задан вектор нормали плоскости = и одна из принадлежащих ей точек , то общее уравнение плоскости имеет вид:

.

2). В нашем случае заданы: вектор нормали =(5, 0,–3), (0,0,0). Тогда можем записать общее уравнение плоскости :

, или .

Ответ: общее уравнение плоскости :.

Пример 2–915: Точка(2,–1,–1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости.

Решение:

1). Задача отличается от предыдущей тем, что вектор нормали плоскости формируется с участием точки, принадлежащей плоскости. По условию отрезок перпендикулярен плоскости . Это значит, можно принять: вектор . Вычисление вектора обычное: == (2,–1,–1); в качестве точки примем точку .

2). Используя полученные параметры, запишем общее уравнение плоскости :

, или .

Ответ: общее уравнение плоскости :.

Пример 3–918: Доказать, что уравнение плоскости, проходящей через точкупараллельно векторами, может быть представлено в виде:

Замечание: еще раз вспомним, что при решении задач аналитической геометрии важно применять (по возможности!) как «чисто аналитические» средства (не опираясь на детали геометрического смысла решений) так и, напротив, с максимальным привлечением возможностей геометрии. В связи с этим рассмотрим два варианта решений.

Решение:

Геометрические штрихи:

1). Обозначим плоскость с точкой как. По условию плоскостьпараллельна векторами. Векторыиможно было бы привести к точке(векторы,свободные!). Мы покажем эти векторы в плоскостяхи.

2). Из построений следует, что вектор , построенный для произвольной точки плоскости, должен быть таким, что векторы,,компланарны.

Для доказательства формулы, указанной в задании, применим способы: формально логический и максимально учитывающий геометрические особенности участвующих фигур.

Вариант-1 (формально алгебраический):

Известно, что условие компланарности векторов , , можно записать, используя смешанное произведение этих векторов:

. (S)

Если обозначить: =, где , то равенство: (S) есть общее уравнение плоскости, имеющей вектор нормалии проходящей через точку.

Вариант-2 (учитывает свойства геометрических фигур):

Составим векторные произведения: =и=; если векторыине параллельны, то при доказательстве будем использовать вектор, иначе.

1). Пусть: ==0. Так как вектор перпендикулярен плоскости , то . Тогда имеем: ===0, то есть смешанное произведение векторов , , равно нулю, а это и есть условие (S).

2). Пусть вектор =0 – это значит: ||, то есть эти векторы коллинеарны. В этом случае можно использовать вектор =0. Учитывая перпендикулярность векторов и , записать ·=·==0. Условие (S) и в этом случае выполняется.

Формально, алгебраически случаи 1) и 2) не различимы: в обоих случаях имеем . Но, геометрические последствия в случае 2) существенно другие: все коэффициенты в уравнении плоскости (S) равны нулю (так как ||). Это значит, что равенство (S) выполняется для любой точки пространства: . Парадокс?

Оказывается в случае 2) нам подойдёт любая плоскость, которая содержит точку и проходящую через неё прямую, параллельную вектору (или ). А как определить эту плоскость? Обращаемся к уравнению: пучок плоскостей!

Используя геометрические особенности рассматриваемого случая 2), построим уравнение пучка плоскостей:

A. Определим плоскостьтремя точкамии плоскостьточками:, причем:=+, а точкии– произвольные. Очевидно, линией пересечения плоскостейиявляется прямая линия.

B. Пусть имеем уравнения:и:. Воспользуемся полученным ранее уравнением пучка плоскостей:

: +=0,

или в форме: :+++=0.

Конкретные значения параметров и(их отношение!) определяют по дополнительной информации, выделяющей из пучка заданную плоскость. Так как по условию плоскостиипересекаются, то коэффициенты при переменныхне могут одновременно обратиться в нуль, и для любых пар значенийипредставленные уравнения определяет некоторую плоскость!

Вывод: использование только аналитических построений не всегда приводит к определенным геометрическим образам!

Ответ: Доказано!

Пример 4–924: Установить, какие из следующих пар уравнений определяют параллельные плоскости: 1):;:;

2) :;:;

3) :;:.

Решение:

Общее: Если плоскости и параллельны, то ||. Проверим это условие в каждом варианте.

1). Составим векторы: =(2,–3,5) и =(2,–3,5): || → ||.

2). Составим векторы: =(4, 2, –4) и =(2, 1,2) – не параллельны → и пересекаются.

3). Составим векторы: =(1, 0, –3) и =(2, 0, –6): || → ||.

Ответ: плоскости: 1) параллельны; 2) пересекаются; 3) параллельны.

Пример 5–943: Найти точки пересечения плоскости:с осями координат.

Решение:

Общее: рисунок не отражает фактическое расположение заданной плоскости: его назначение создать общий геометрический образ для решения задачи!

Воспользуемся общим способом решения задачи:

1). Учтем, что ось : =0, =0. Тогда из уравнения плоскости → =12.

2). Учтем, что ось : =0, =0. Тогда из уравнения плоскости → = –8.

3). Учтем, что ось : =0, =0. Тогда из уравнения плоскости → = –6.

Ответ: (12,0,0), (0, –8,0), (0,0, –6).

Пример 6–944: Дано уравнение плоскости:. Написать для нее уравнение в отрезках.

Решение:

1). Учтем формулы: =, =,= и составим уравнение: , которое называют уравнением в отрезках.

2). В нашем случае: =, =, = и тогда: .

Ответ: .

Пример 7–957-1: Дано уравнение плоскости:. Привести уравнение плоскостик нормальному виду.

Решение:

1). Если уравнение плоскости задано в общем виде: , то его можно «нормировать», то есть привести к нормальному виду: . Для этого: умножим общее уравнение на число : так, что получается нормальное уравнение. Это значит:

→; → (S)

2). Воспользуемся выражениями (S):

; так как D<0, то → – нормальное уравнение.

Ответ: уравнение:

Пример 8–965: Две грани куба лежат на плоскостях:и:. Вычислить объем этого куба.

Решение:

С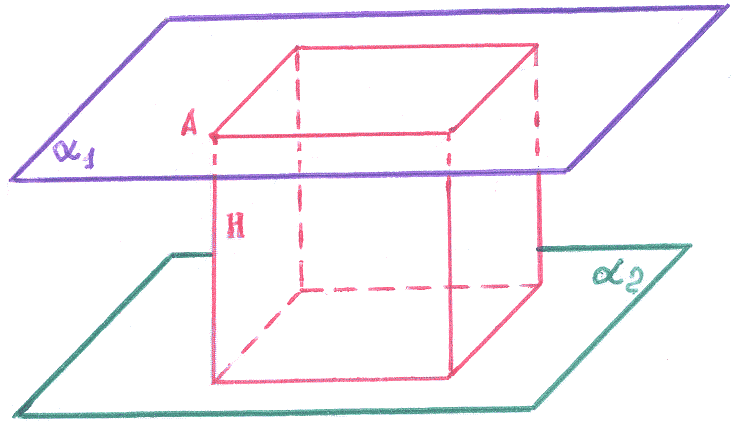хема решения задачи: 1) для вычисления объёма куба необходимо вычислить расстояние между его противоположными (параллельными) гранями; 2) учитывая определение расстояния между параллельными плоскостями, вычислим расстояние произвольной точки плоскости до плоскости .

1). Выделим в плоскости произвольную точку (0,0,1).

2). Нормализуем уравнение плоскости : .

3). Вычислим отклонение точки от плоскости : ==–2. Это значит, что длина ребра куба =2, а объём =8.

Ответ: =8 куб. ед.

Пример 9–985: Доказать, что прямая:пересекает ось.

Решение:

Общее: Линия пересечения заданных плоскостей состоит из общих точек плоскостей: обозначим как . Обозначим прямую, которую должна пересекать прямая , как . В нашем случае примем: =. Это значит, что на оси имеется общая точка плоскостей.

1). Найдём точку пересечения плоскости с осью . Так как на оси имеем значения: =0, =0, легко получаем: (0,–2,0).

2). Найдём точку пересечения плоскости с осью . Так как на оси имеем значения: =0, =0, легко получаем: (0,–2,0).

3). Так как =, то линия пересечения заданных плоскостей пересекает ось .

Ответ: Доказано.

Пример 10–1007: Составить каноническое уравнение прямой, проходящей через точку(2,0,–3) параллельно: 1) вектору=(2, –2,5); 2) прямой:; 3) оси; 4) оси; 5) оси.

Решение:

Каноническое уравнение прямой : , где – точка, принадлежащая прямой, – направляющий вектор прямой. Тогда заданные варианты записываем так:

1). ; 2). ; 3) ;

4). ; 5) .

Ответ: подробно в тексте.

Пример 11–1008: Составить каноническое уравнение прямой, проходящей через две данные точки: 1)(1,–2,1),(3,1,–1); 2)(3,–2,0),(1,0,–3); 3)(0,–2,3),(3,–2,1); 4)(1,2,–4),(–1,2,–4).

Решение:

Определим вектор – направляющий вектор прямой, и канонические уравнения прямой для заданных вариантов записываем так:

1). ; 2). ;

3) ; 4). .

Ответ: подробно в тексте.

☻

1. При помощи какого свойства векторов получают общее уравнение плоскости?

2. Как записывается уравнение плоскости, проходящей через заданную точку?

3. Что значит «уравнение плоскости в отрезках»?

4. Как получают каноническое уравнение прямой линии в пространстве?

5. Какой физический смысл имеет параметрическое задание уравнения прямой в пространстве?

6. Как получают уравнение прямой, проходящей через две заданные точки?

7. Что такое «отклонение» точки от заданной плоскости, как его вычисляют?

8. Как нормализовать общее уравнение плоскости?

9. Как определить угол между заданными прямыми линиями в пространстве?

10. Как записывают условия параллельности и перпендикулярности для двух прямых в пространстве?

11. Какие задачи в пространстве вызвали наибольший интерес (восторг!)?

Задачи для самоподготовки:

Пример 1–916: Даны точки(3,–1,2) и(4,–2,–1). Составить уравнение плоскости, проходящей через точкуперпендикулярно вектору.

Ответ: плоскость :.

Пример 2–917: Составить уравнение плоскости, проходящей через точку(3,4,–5), параллельно векторам=(3, 1,–1) и=(1, –2,1).

Ответ: плоскость :.

Пример 3–923: Определить координаты какого-нибудь нормального вектора каждой из следующих плоскостей. В каждом случае написать общее выражение координат произвольного нормального вектора: 1):; 2):; 3):; 4):; 5):; 6):.

Ответ: векторы: 1) =·(2, –1,–2); 2)=·(1, 5,–1); 3)=· (3,–2, 0);

4) = ·(0, 5, –3); 5) =·(1, 0, 0); 6) =·(0, 1, 0).

Пример 4–925: Установить, какие из следующих пар уравнений определяют перпендикулярные плоскости: 1):;:;

2) :;:;

3) :;:.

Ответ: плоскости: 1) перпендикулярны; 2) перпендикулярны; 3) не перпендикулярны.

Пример 5–945: Найти отрезки, отсекаемые плоскостью:от координатного угла.

Ответ: отсекаемые отрезки: на оси :=–4; на оси:= 3.

Пример 6–946: Вычислить площадь треугольника, отсекаемого от координатного углаплоскостью:.

Ответ: площадь треугольника: =240 кв.ед.

Пример 7–957-3,4: Даны плоскости:и:. Привести уравнения плоскостейик нормальному виду.

Ответ: уравнения плоскостей :и:.

Пример 8–966: На осинайти точку, отстоящую от плоскости:на расстояние= 4.

Ответ: точки: (0, –5, 0) и(0, 7, 0).

Пример 9–986: При каком значенииdпрямая:пересекает: 1)ось; 1)ось; 1)ось.

Ответ: 1): =–4, 2):=9, 3):=3.

Пример 10–1010: Составить параметрические уравнения прямой, проходящей через данные точки: 1)(3,–1,2),(2,1,1); 2)(1,1,–2),(3,–1,0); 3)(0,0,1),(0,1,–2).

Ответ: уравнения: 1) , 2), 3).

< * * * * * >