§ 3. Гиперболический параболоид.

К поверхностям 2-го порядка относится также гиперболический параболоид. Эта поверхность не может быть получена применением алгоритма использующего вращение некоторой линии относительно неподвижной оси.

Для построения гиперболического параболоида используется специальная модель. Эта модель включает в себя две параболы, располагающиеся в двух взаимно перпендикулярных плоскостях.

Пусть парабола I располагается в плоскости и неподвижна. Парабола II совершает сложное движение:

▫ её начальное положение совпадает с плоскостью , причём вершина параболы совпадает с началом координат: =(0,0,0);

▫ далее эта парабола совершает движение параллельный перенос, причём её вершина совершает траекторию, совпадающую с параболой I;

▫ рассматривается два различных начальных положения параболы II: один – ветви параболы вверх, второй – ветви вниз.

Запишем уравнения: для первой параболы I: – неизменно; для второй параболы II: – начальное положение, уравнение движения: Нетрудно видеть, что точка имеет координаты: . Так как необходимо отобразить закон движения точки : эта точка принадлежит параболе I, то должны постоянно выполняться соотношения: = и .

Из геометрических особенностей модели легко видеть, что подвижная парабола заметает некоторую поверхность. В таком случае уравнение поверхности, описываемой параболой II, имеет вид:

или→. (1)

Форма получаемой поверхности зависит от распределения знаков параметров . Возможны два случая:

1). Знаки величин p и q совпадают: параболы I и II располагаются по одну сторону от плоскости OXY. Примем: p = a² и q = b² . Тогда получаем уравнение известной поверхности:

→ эллиптический параболоид. (2)

2). Знаки величин p и q различны: параболы I и II располагаются по разные стороны от плоскости OXY. Пусть p = a² и q = -b² . Теперь получаем уравнение поверхности:

→гиперболический параболоид. (3)

Представить геометрическую форму поверхности, определяемой уравнением (3) нетрудно, если вспомнить кинематическую модель взаимодействия двух парабол, участвующих в движении.

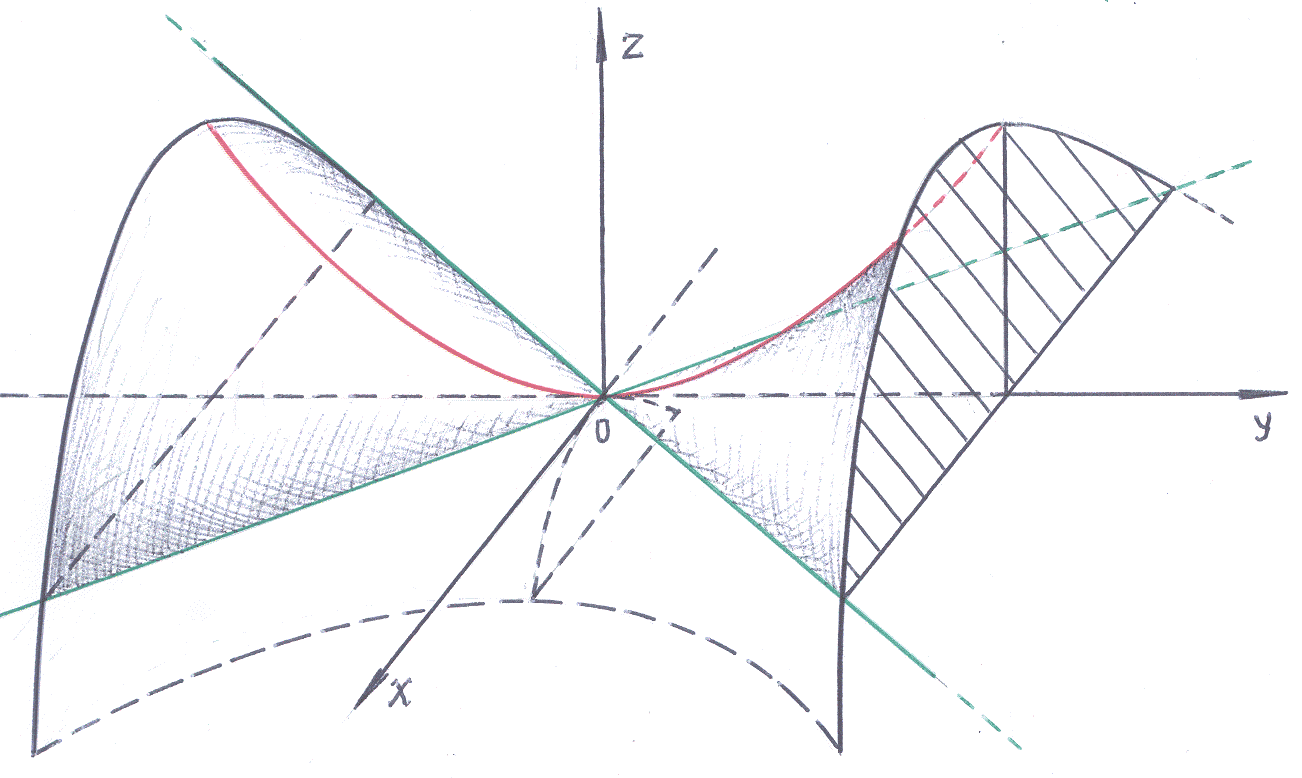
На рисунке красным цветом условно показана парабола I. Показана только окрестность поверхности у начала координат. Из-за того, что форма поверхности выразительно намекает на кавалерийское седло, окрестность эту часто называют – седло.

В физике, при исследованиях устойчивости процессов, вводят типы равновесия: устойчивое – лунка, выпуклостью вниз, неустойчивое – выпуклая вверх поверхность и промежуточное – седло. Равновесие третьего типа также относят к типу неустойчивого равновесия, причём только на красной линии (парабола I) возможно равновесие.

§ 4. Цилиндрические поверхности.

При рассмотрении поверхностей вращения мы определили простейший цилиндрическую поверхность – цилиндр вращения, то есть круговой цилиндр.

В элементарной геометрии цилиндр определён по аналогии с общим определением призмы. Оно достаточно сложное:

▫ пусть имеем в пространстве плоский многоугольник – обозначим как , и с ним совпадает многоугольник – обозначим как ;

▫ применим к многоугольнику движение параллельный перенос: точки перемещаются по траекториям, параллельным заданному направлению ;

▫ если остановить перенос многоугольника , то его плоскость параллельна плоскости ;

▫ поверхностью призмы называют: совокупность многоугольников , – основания призмы, а также параллелограммов , ,... – боковая поверхность призмы.

Воспользуемся элементарным определением призмы для построения более общего определения призмы и её поверхности, а именно, будем различать:

▫ неограниченная призма – это многогранное тело, ограниченное рёбрами ,,... и плоскостями между этими рёбрами;

▫ ограниченная призма – это многогранное тело, ограниченное рёбрами ,,... и параллелограммами , ,...; боковая поверхность этой призмы – совокупность параллелограммов , ,...; основания призмы – совокупность многоугольников ,.

Пусть имеем неограниченную призму: ,,... Пересечём эту призму произвольной плоскостью . В сечении получим многоугольник . Пересечём эту же призму другой плоскостью . В сечении получим многоугольник . В общем случае считаем, что плоскость не параллельна плоскости . Это значит, призма построена не параллельным переносом многоугольника .

Предложенное построение призмы включает не только прямые и наклонные призмы, но и любые усечённые.

В аналитической геометрии цилиндрические поверхности будем понимать настолько обобщённо, что неограниченный цилиндр включает неограниченную призму как частный случай: стоит лишь предположить, что многоугольник можно заменять произвольной линией, не обязательно замкнутой – направляющая цилиндра. Направление называют образующей цилиндра.

Из всего сказанного следует: для определения цилиндрической поверхности необходимо задать линию-направляющую и направление образующей.

Цилиндрические поверхности получают на основе плоских кривых 2-го порядка, служащих направляющими для образующих.

На начальном этапе изучения цилиндрических поверхностей примем упрощающие допущения:

▫ пусть направляющая цилиндрической поверхности всегда располагается в одной из координатных плоскостей;

▫ направление образующей совпадает с одной из осей координат, то есть перпендикулярна плоскости, в которой определена направляющая.

Принятые ограничения не приводят к потере общности, так как остаётся возможность за счёт выбора сечений плоскостями и строить произвольные геометрические фигуры: прямые, наклонные, усечённые цилиндры.

Эллиптический цилиндр.

Пусть в качестве направляющей цилиндра взяли эллипс : , расположенный в координатной плоскости , а направление образующей определяет ось . В этом случае уравнение цилиндра – это сама линия : эллиптический цилиндр.

Гиперболический цилиндр.

Пусть в качестве направляющей цилиндра взяли гиперболу : , расположенную в координатной плоскости , а направление образующей определяет ось . В этом случае уравнение цилиндра – это сама линия : гиперболический цилиндр.

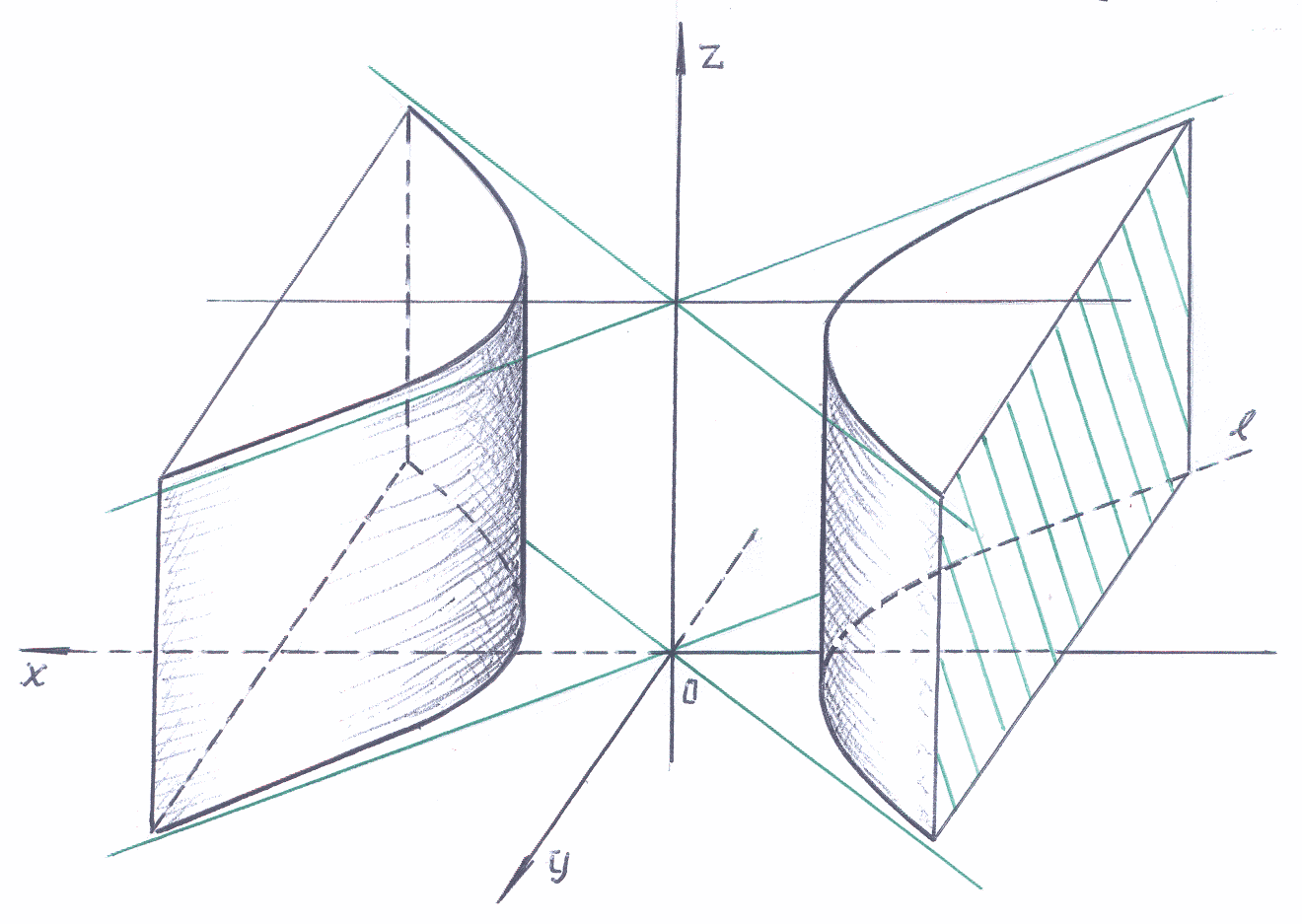
Параболический цилиндр.

Пусть в качестве направляющей цилиндра взяли гиперболу : , расположенную в координатной плоскости , а направление образующей определяет ось . В этом случае уравнение цилиндра – это сама линия : параболический цилиндр.

Замечание: учитывая общие правила построения уравнений цилиндрических поверхностей, а также представленные частные примеры эллиптического, гиперболического и параболического цилиндров, отметим: построение цилиндра для любой другой образующей, для принятых упрощающих условий, не должно вызвать никаких затруднений!

Рассмотрим теперь более общие условия построения уравнений цилиндрических поверхностей:

▫ направляющая цилиндрической поверхности располагается в произвольной плоскости пространства ;

▫ направление образующей в принятой системе координат произвольно.

Принятые условия изобразим на рисунке.

В соответствии с рисунком будем считать:

▫ направляющая цилиндрической поверхности располагается в произвольной плоскости пространства ;

▫ система координат получена из системы координат параллельным переносом;

▫ расположение направляющей в плоскости наиболее предпочтительное: для кривой 2-го порядка будем считать, что начало координат совпадает с центром симметрии рассматриваемой кривой;

▫ направление образующей произвольное (может быть задано любым из способов: вектором, прямой и др.).

В дальнейшем будем считать, что системы координат и совпадают. Это означает, что 1-й шаг общего алгоритма построения цилиндрических поверхностей, отражающий параллельный перенос: → , предварительно выполнен.

Напомним, как учитывается параллельный перенос в общем случае, рассмотрев простой пример.

☺☺

Пример 6–13: В системе координат задано уравнение направляющей цилиндра в виде: =0. Записать уравнение этой направляющей в системе .

Решение:

1). Обозначим произвольную точку : в системе как , и в системе как .

2). Запишем векторное равенство: =+. В координатной форме это можно записать в виде: =+. Или в виде: =–, или: =.

3). Запишем уравнение направляющей цилиндра в системе координат :

=0.

Ответ: преобразованное уравнение направляющей: =0.

☻

Итак, будем считать, что центр кривой, представляющей направляющую цилиндра, всегда располагается в начале координат системы в плоскости .

Рис. В. Базовый рисунок при построении цилиндра.

Сделаем ещё одно допущение, упрощающее заключительные шаги построения цилиндрической поверхности. Так как применением вращения системы координат нетрудно совместить направление оси системы координат с нормалью плоскости , а направления осей и с осями симметрии направляющей , то будем считать, что в качестве исходного положения направляющей имеем кривую, расположенную в плоскости , причём одна её ось симметрии совпадает с осью , а вторая с осью .

Замечание: так как выполнение операций параллельный перенос и вращение вокруг неподвижной оси операции достаточно простые, то принятые допущения не сужают применимость разрабатываемого алгоритма построения цилиндрической поверхности в самом общем случае!

Мы видели, что при построении цилиндрической поверхности в случае, когда направляющая располагается в плоскости , а образующая параллельна оси , достаточно определить только направляющую .

Так как цилиндрическая поверхность может быть однозначно определена заданием любой линии, получаемой в сечении этой поверхности произвольной плоскостью, то примем такой общий алгоритм решения задачи:

1^▫. Пусть направление образующей цилиндрической поверхности задано вектором . Спроектируем направляющую , заданную уравнением: =0, на плоскость, перпендикулярную направлению образующей , то есть на плоскость . В результате цилиндрическая поверхность будет задана в системе координат уравнением: =0.

2^▫. Применим вращение системы координат вокруг оси на угол : смысл угла вполне понятен из рисунка. В результате вращения система координат совместится с системой , а уравнение конической поверхности преобразуется в уравнение: =0.

3^▫. Применим вращение системы координат вокруг оси на угол : смысл угла вполне понятен из рисунка. В результате вращения система координат совместится с системой , а уравнение конической поверхности преобразуется в =0. Это и есть уравнение цилиндрической поверхности, у которой были заданы направляющая и образующая в системе координат .

Представленный ниже пример иллюстрирует реализацию записанного алгоритма и вычислительные трудности подобных задач.

☺☺

Пример 6–14: В системе координат задано уравнение направляющей цилиндра в виде: =9. Составить уравнение цилиндра, образующие которого параллельны вектору =(2,–3,4).

Решение:

1). Спроектируем направляющую цилиндра на плоскость, перпендикулярную . Известно, что такое преобразование заданную окружность превращает в эллипс, осями которого будут: большая =9, а малая =.

Этот рисунок иллюстрирует проектирование окружности, заданной в плоскости на координатную плоскость .

2). Результатом проектирования окружности является эллипс: =1, или . В нашем случае это: , где ==.

3). Итак, уравнение цилиндрической поверхности в системе координат получено. Так как по условию задачи мы должны иметь уравнение этого цилиндра в системе координат , то остаётся применить преобразование координат, переводящее систему координат в систему координат , заодно и уравнение цилиндра: в уравнение, выраженное через переменные .

4). Воспользуемся базовым рисунком, и запишем все необходимые для решения задачи тригонометрические значения:

==,==,==.

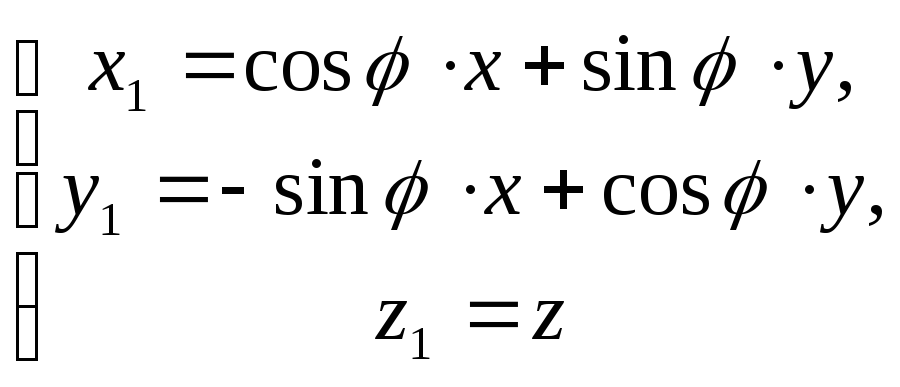5). Запишем формулы преобразования координат при переходе от системы к системе : (В)

6). Запишем формулы преобразования координат при переходе от системы к системе : (С)

7). Подставляя переменные из системы (В) в систему (С), а также учитывая значения используемых тригонометрических функций, запишем:

==.

==.

8). Остаётся подставить найденные значения и в уравнение направляющей цилиндра : в системе координат . Выполнив аккуратно все алгебраические преобразования, получаем уравнение конической поверхности в системе координат : =0.

Ответ: уравнение конуса: =0.

Пример 6–15: В системе координат задано уравнение направляющей цилиндра в виде: =9, =1. Составить уравнение цилиндра, образующие которого параллельны вектору =(2,–3,4).

Решение:

1). Нетрудно заметить, этот пример отличается от предыдущего только тем, что направляющую параллельно перенесли на 1 вверх.

2). Это значит, что в соотношениях (В) следует принять: =–1. Учитывая выражения системы (С), скорректируем запись для переменной :

=.

3). Изменение легко учитывается коррекцией конечной записи уравнения для цилиндра из предыдущего примера:

=0,

или =0,

Ответ: уравнение конуса: =0.

☻

Замечание: нетрудно заметить, что основная трудность при многократных преобразованиях систем координат в задачах с цилиндрическими поверхностями – этоаккуратностьивыносливостьв алгебраических марафонах: да здравствует система образования, принятая в нашей многострадальной стране!