235

АГ: Глава 6

Глава 6. Тела вращения. Общее уравнение поверхности второго порядка.

Изучение поверхностей второго порядка представляет интерес, прежде всего, тем, что они широко применяются в инженерной практике. Это определяется технологичностью этих геометрических фигур. Важно и то, что аналитические модели указанных фигур достаточно просты, и оптимизационные задачи при построении различных технических конструкций с использованием поверхностей второго порядка решаются достаточно просто.

Поверхности второго порядка также широко применяются для получения пространственных кривых.

В математическом анализе при изучении кратных, криволинейных, поверхностных интегралов также необходимы сведения из раздела аналитической геометрии: поверхности второго порядка.

Наиболее простой аналитической модельюгеометрической фигуры поверхность можно считать уравнение:

. (1)

Совокупность всех пар числовых значений , при которых получает действительное значение, называется областью определения переменной , заданной уравнением (1).

Пусть имеем прямоугольную систему координат . Рассмотрим в плоскости область , из которой можно произвольно выбирать точки . В каж­дой точке восставим перпендикуляр к плоскости и отложим на нём отрезок , равный соответствующему значению . Совокупность всех точек = образует не­ко­то­рую поверхность. Будем говорить: уравнение определяет в пространстве поверхность.

Определение: (6.1)

Поверхностью будем называть совокупность точек пространства, координаты которых удовлетворяют уравнению вида: .

Уравнение есть частный случай уравнения . В настоящей главе будет рассмотрен частный случай поверхностей – поверхности 2-го порядка.

Выделим возможные случаи, когда область определения :

▫ содержит бесчисленное множество точек;

▫ содержит конечное число точек (в частном случае одну точку);

▫ не содержит ни одной точки: в этом случае поверхность называют мнимой.

В зависимости от вида уравнения различают поверхности:

▫ алгебраические: в этом случае – многочлен - ой степени, или в результате определённого числа алгебраических преобразований может быть приведён к форме многочлена - ой степени;

▫ трансцендентные: в этом случае – любая, не приводимая к форме многочлен - ой степени, функция.

Рассмотрим случай, когда в пространстве задано уравнение: . Что это значит? Какой геометрический образ соответствует этому уравнению?

Учитывая выражение , можем считать, что на плоскости определена линия, причём переменные равноправны: можно считать независимой переменной , тогда ; или – независимая переменная, а . А какова роль ? Считают, что для любой пары чисел переменная может принимать любое значение!

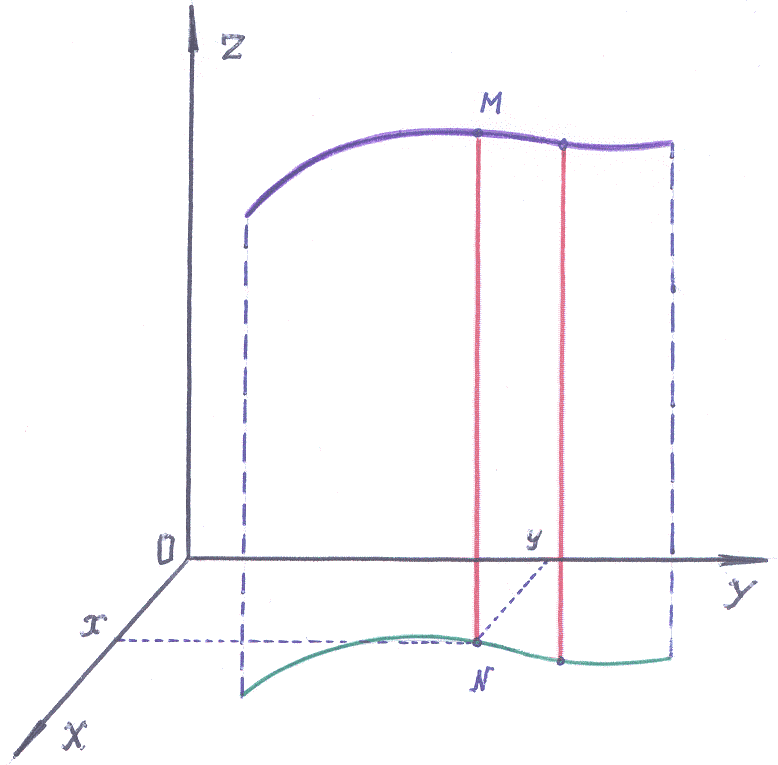Итак, в плоскости расположена линия . Пусть точка – одна из точек этой линии. В каж­дой точке восставим перпендикуляр к плоскости . На этом перпендикуляре отметим произвольную точку . Этой точке поставим в соответствие тройку чисел: – координаты точки . В таком случае будем говорить, что нами построена цилиндрическая поверхность.

В связи с рассмотренными, возможными видами уравнений: и возникают две задачи:

1). Дано уравнение с тремя неизвестными: . Необходимо исследовать форму поверхности, соответствующей этому уравнению.

2). Дана поверхность как геометрическое место точек, обладающих некоторым общим свойством. Необходимо составить уравнение этой поверхности.

☺☺

Пример 6–01: Задано геометрическое место точек, равноудалённых от данной точки – сфера. Найти уравнение сферы.

Решение:

1). Точка, относительно которой выделяются точки пространства, называется центром сферы. Обозначим её как . Расстояние от произвольной точки сферы до точки назовём радиусом сферы. Обозначим его как .

2). Определяющее свойство геометрического места точек сфера: =, или =:

= – уравнение сферы.

3). В частном случае, когда центр сферы совпадает с началом координат, уравнение сферы имеет простейший вид: = – каноническое уравнение сферы.

Ответ: уравнение общее: =, каноническое: =.

☻

При рассмотрении различных систем координат была определена специальная система координат: сферическая. Возникает вопрос: как её использовать при построении уравнения сферы?

В соответствии с определением сферы необходимо на луче, имеющем произвольное направление, выделить точку, находящуюся на расстоянии от начала координат (0,0,0). Для однозначного определения направления луча в пространстве выполним (в соответствии с рисунком) построение: из произвольной точки, принадлежащей сфере, опустим на плоскость перпендикуляр: его основание отметим как точку .

Точки определяют плоскость. Обозначим угол между плоскостью и как угол . Определим также угол между осью координат и лучом как угол .

В соответствии с аксиомами об измерении угла между двумя прямыми и двумя плоскостями направление луча однозначно определяется заданием величин углов: и .

В соответствии с аксиомами измерения длины отрезка положение точки на луче , то есть на сфере, также определится однозначно. Это значит, мы имеем систему координат для любой точки сферы.

Постоянными элементами, относительно которых определяется положе­ние любой точки сферы, являются полюс – точка , полярная ось – ось , полярная полуплоскость – плоскость , радиус сферы .

Обычно будем считать, что угол изменяется в диапазоне: , угол изменяется в диапазоне: , а расстояние точки до полюса O – постоянная величина.

Используя рисунок, нетрудно записать выражения для перехода от сферических координат к прямоугольным декартовым координатам:

1). От сферических координат к декартовым координатам: (2)

2). От декартовых координат к сферическим координатам:

, , , . (3)

Замечания: 1) из выражений (3) необходимо учитывать и выражение для косинуса, и выраже­ние для синуса, так как только так можно однозначно определить по­ложение луча, содержащего выделенную точку;

2) следует учесть также, для на­чала координат (=0) из выра­жений (3) углы опреде­лить не удаётся: нару­шается взаимно однозначное соответствие систем коорди­нат;

3) специальные системы координат часто применяют в физике; эффективно их при­меняют и в математическом анализе.

Уравнения (2) называют параметрическими уравнениями сферы. Обобщая это понятие, будем уравнения вида: (4)

называть параметрическими уравнениями поверхности, переменные называют параметрами поверхности.

Итак, мы определили в пространстве произвольную поверхность и её частный случай цилиндр. А как в пространстве задать линию?

Линию в пространстве можно определить как геометрическое место точек, принадлежащих одновременно двум поверхностям – линия пересечения поверхностей:

(5)

Если линию в пространстве рассматривать как траекторию движения точки, то удобно рассматривать координаты точки как некоторые функции вспомогательного параметра, в физике обычно в качестве параметра используют время:

, , – параметрические уравнения линии. (6)

Рассмотрим один из примеров получения параметрических уравнений линии, определяя свойства геометрического места точек через описание геометрических и кинематических характеристик.

☺☺

Пример 6–02: Отрезок длины вращается с постоянной угловой скоростью вокруг оси , сохраняя перпендикулярность к этой оси. Одновременно отрезок с постоянной скоростью перемещается вдоль оси в положительном направлении. Найти уравнение линии, описываемой концом отрезка .

Решение:

1). Так как отрезок при вращении сохраняет длину, то точка перемещается по поверхности цилиндра радиуса . Примем за начальное положение точки : =, =0, =0.

2). Используя формулы из тригонометрии, для заданных начальных условий, легко получаем: ,

3). Так как движение отрезка вдоль оси происходит с постоянной скоростью, то, учитывая начальное положение точки , для координаты получим: =·.

4). Оформляя полученные результаты в виде системы параметрических уравнений, имеем:

(6.1)

5). Система (6.1) представляет параметрические уравнения винтовой линии. По отношению к винтовой линии применяют понятие шаг винтовой линии: перемещение точки вдоль оси за один оборот вокруг этой оси. Один оборот соответствует углу 2. Это значит, что =2. Отсюда определяем время одного оборота: =. После чего легко вычисляем шаг винтовой линии: =.

Ответ: уравнение линии: – параметрические уравнения винтовой линии.

☻