§ 2. Общие свойства кривых второго порядка.

Директрисы кривых второго порядка. Все кривые 2-го порядка имеют директрису: прямая, по отношению к которой эллипс, гипербола и парабола имеют особые свойства. Использование директрисы в случае параболы мы видели в самом определении параболы.

При получении канонических уравнений эллипса, гиперболы и параболы было установлено понятие эксцентриситета – , причём:

а). < 1 → для эллипса; б). = 1 → для параболы; в). > 1 → для гиперболы.

Общее определение. Кривой второго порядка называют геометрическое место точек плоскости, обладающих свойством: расстояние от точки до точки , называемой фокусом, равно расстоянию точки до прямой , называемой директрисой, умноженному на некоторое число – эксцентриситет.

Замечание: Определение кривых 2-го порядка с использованием директрисы не позволяет принять =0, хотя раньше такое значение эксцентриситета выделяло частный случай эллипса – окружность!

Из общего определения кривых второго порядка с использованием директрисы и эксцентриситета следует: директриса и кривая второго порядка не могут пересекаться!

О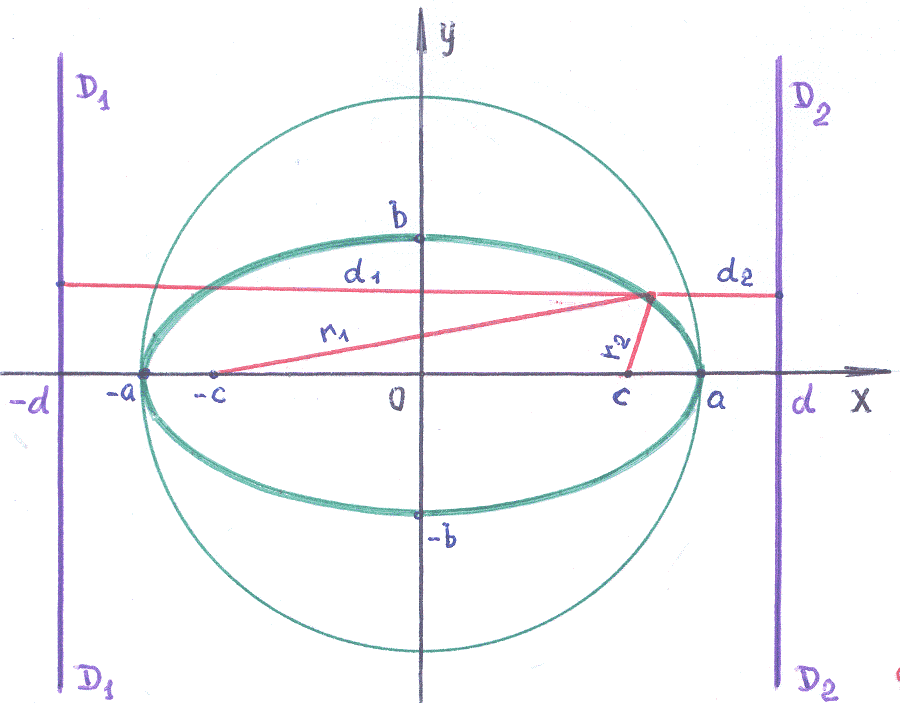пределим директрису для эллипса.

При рассмотрении канонического уравнения эллипса было установлено: кривая симметрична относительно осей и . Это означает, что эллипс должен иметь две, симметрично расположенные относительно оси , директрисы. Обозначим эти директрисы, как и .

В соответствии с определением, для левой директрисы имеем: =·. Но, для эллипса: = и =. Легко видеть, что в этом случае: . Это значит, что и уравнение левой директрисы: .

Для правой директрисы: = и =. Используя условие: =·, получаем такое же значение параметра: и уравнение правой директрисы: .

Если учесть, что для эллипса <1, то . Это подтверждает предположение, что кривая и директриса не пересекаются!

Определим директрису для гиперболы.

П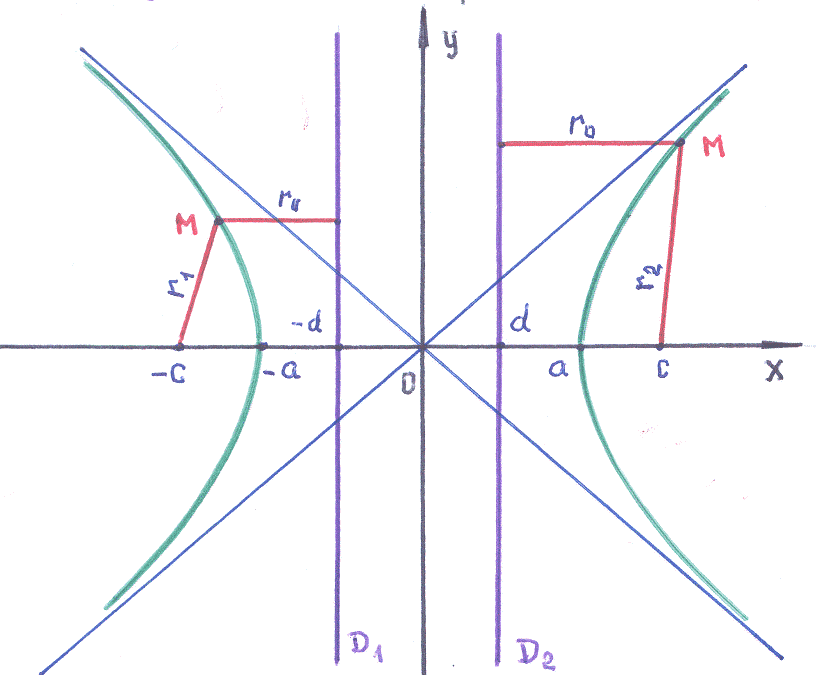ри рассмотрении канонического уравнения гиперболы было установлено: кривая симметрична относительно осей и . Это означает, что гипербола должна иметь две, симметрично расположенные относительно оси , директрисы. Обозначим эти директрисы, как и .

В соответствии с определением, для левой директрисы имеем: =·. Но, для левой ветви гиперболы было получено: =, а =. Легко видеть, что в этом случае: . Это значит, что и уравнение левой директрисы: .

Для правой директрисы: = и =. Используя условие: =·, получаем такое же значение параметра: и уравнение правой директрисы: .

Если учесть, что для гиперболы >1, то . Это подтверждает предположение, что кривая и директриса не пересекаются!

☺☺

Пример 5–09: Дан эллипс: . Определить его полуоси, фокусы, эксцентриситет и директрисы.

Решение:

1). Приведём заданное уравнение эллипса к канонической форме: .

2). Тогда: =5, =3, и можно вычислить: =4, ==, после чего: ==.

Ответ: полуоси: =5, =3, фокусы: (–4,0) и (4,0), =, директрисы: =.

Пример 5–10: Составить уравнение гиперболы, если её фокусы лежат на оси симметрично относительно начала координат и заданы:

1) точки (6,–1) и (–8,2), лежащие на гиперболе;

2) точка (–3, ) и уравнения директрис: x=.

Решение:

1). Воспользуемся уравнением гиперболы: и учтём, что точки и лежат на кривой. Для точки : , для точки : . Решая полученную систему уравнений, получаем: ,. Уравнение гиперболы: .

2). Воспользуемся уравнением гиперболы и учтём, что точка лежит на гиперболе: . Учитывая: =, из уравнения директрисы получаем: =, откуда: =.

3). Далее воспользуемся выражением для гиперболы: , или . Если подставить значения и в уравнение: , то получим уравнение относительно : , из которого следует =3 и =.

4). Для =3 вычисляем: =4 и =5. Тогда уравнение гиперболы: .

5). Если =, то: = и =. В этом случае гипербола: .

Ответ: в случае 1) ; в случае 2) , или .

☻

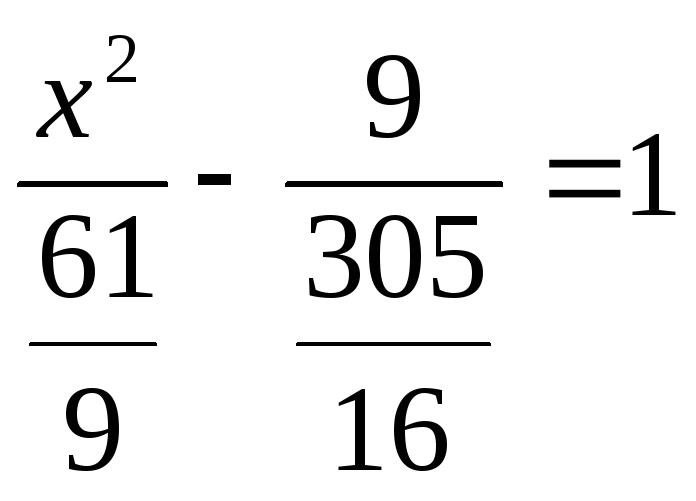Диаметры кривых второго порядка. Продолжим исследование кривых второго порядка, используя общее для этих кривых уравнение: . Из этого уравнения получаем:

Окружность: при ==1, =0, =–; эллипс: при =, =, =0, =–1.

Гипербола: при =, =–, =0, =–1; парабола: при =0, =1, =– p, =0.

Уравнение будем использовать для решения вопросов о диаметрах и касательных для эллипса, гиперболы и параболы.

Если кривую 2-го порядка пересекать прямыми, параллельными :, то получим хорды с угловым коэффициентом . Если на каждой хорде выделить середину, то (оказывается!) все эти средние точки лежат на одной прямой . Эту прямую называют диаметром кривой второго порядка, сопряжённым хордам направления k.

Обозначим концы хорд: и , а точка – середина хорды. Тогда, воспользовавшись формулами для вычисления координат середины отрезка, получим:

=, =. (19)

Так как точки и принадлежат кривой, то, используя общее уравнение, можем записать: и . Составим разность последних равенств: . (20)

Рассмотрим два случая:

1). Пусть 0. Разделим равенство (20) на 2: . Учитывая, что – угловой коэффициент прямой, получаем: . Если параметр 0, то последнее равенство есть прямая. Если =0, но 0, то равенство – тоже есть прямая, именно диаметр кривой второго порядка.

2). Пусть =0: это значит, что хорды параллельны оси . В этом случае 0, и из уравнения (20) следует: =0 – ось .

Применим полученные результаты к окружности, эллипсу, гиперболе и параболе, используя их канонические уравнения.

О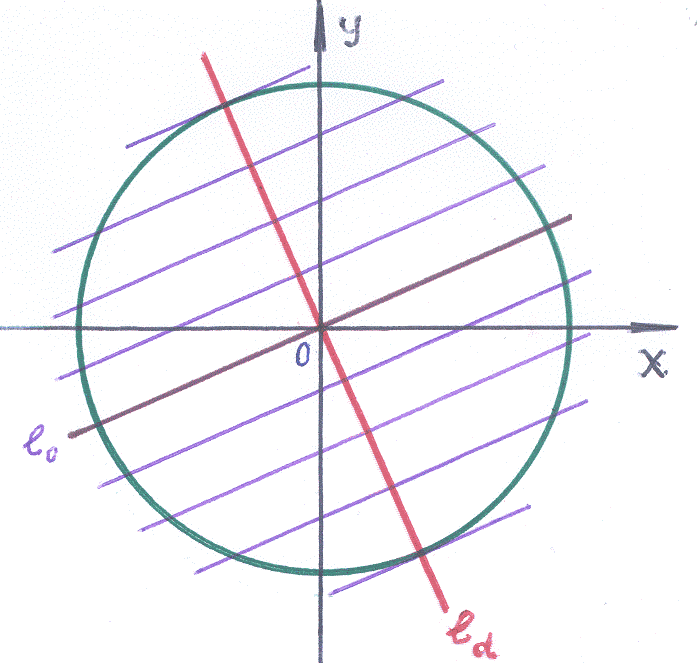пределим диаметры для окружности.

Пусть определяет направления хорд окружности. Учитывая, для окружности коэффициенты общего уравнения кривой второго порядка: ==1, =0, =–, уравнение диаметра окружности принимает вид: , или ==. Так как произведение: =–1, то у окружности хорды и соответствующий им диаметр взаимно перпендикулярны. Отметим также, что диаметр окружности как геометрическое место середин параллельных хорд проходит через начало координат.

Полученный для окружности результат можно было предвидеть, так как в элементарной геометрии было доказано: диаметр окружности, проходящий через середину хорды, ей перпендикулярен!

Определим диаметры для эллипса.

Учитывая, что эллипс – это сжатая окружность, из геометрических соображений можем предположить, что все диаметры эллипса проходят через начало координат .

Пусть определяет направления хорд эллипса. Учитывая, для эллипса коэффициенты общего уравнения кривой второго порядка: =, =, =0, =–1, уравнение диаметра эллипса принимает вид: , или ==. Так как произведение: =– симметрично относительно угловых коэффициентов и , то направления хорд и диаметров взаимно обратимы: если направление хорд определено угловым коэффициентом , то направление диаметров определяется угловым коэффициентом , и наоборот!

Два диаметра, угловые коэффициенты связаны соотношением: =–, называются сопряжёнными.

Нетрудно заметить: если один из сопряжённых диаметров эллипса располагаются в 1-й и 3-й четвертях, то другой будет располагаться во 2-й и в 4-й четвертях.

Если значение углового коэффициента одного из сопряжённых диаметров увеличивается, то есть диаметр вращается против часовой стрелки, то второй вращается в том же направлении. Это совпадает с картиной вращения сопряжённых диаметров окружности.

Сопряжённые диаметры эллипса не могут совпасть: =, так как невозможно равенство: . Если →0, то →. В этом случае сопряжённые диаметры совпадут с осями симметрии эллипса и будут взаимно перпендикулярными.

Определим диаметры для гиперболы.

Пусть определяет направления хорд гиперболы. Учитывая, для гиперболы коэффициенты общего уравнения кривой второго порядка: =, =–, =0, =–1, уравнение диаметра гиперболы принимает вид: , или ==, откуда: =. Так как равенство симметрично относительно угловых коэффициентов и , то направления хорд и диаметров взаимно обратимы: если направление хорд определено угловым коэффициентом , то направление диаметров определяется угловым коэффициентом , и наоборот! Видим также, что угловые коэффициенты и одного знака.

Два диаметра, угловые коэффициенты связаны соотношением: =, называются сопряжёнными. Оба диаметра проходят в одной и той же четверти, причём если увеличивается, то должен уменьшаться. Это значит, что при изменении угловых коэффициентов сопряжённых диаметров гиперболы эти диаметры вращаются в противоположных направлениях.

Так как =, то при значениях = и =. Это значит, что при приближении диаметра к асимптоте сопряжённый диаметр приближается к той же асимптоте.

Если →0, то →. В этом случае получаем взаимно перпендикулярные сопряжённые диаметры, совпадающие с осями гиперболы.

Определим диаметры для параболы.

Пусть определяет направления хорд параболы. Учитывая, для параболы коэффициенты общего уравнения кривой второго порядка: =0, =1, =– p, =0, уравнение диаметра параболы принимает вид: , или = – прямая, параллельная оси . Это значит, что все диаметры параболы параллельны оси .

Если диаметр и хорды перпендикулярны, то диаметр совпадает с осью .

Вывод: общность кривых второго порядка при решении задачи о диаметрах проявляется в том, что все они имеют диаметры и для их нахождения используют одно и то же алгебраическое выражение.

☺☺

Пример 5–11: Дана параллельная ортогональная проекция окружности и её диаметра на некоторую плоскость. Как построить проекцию перпендикулярного диаметра этой окружности?

Р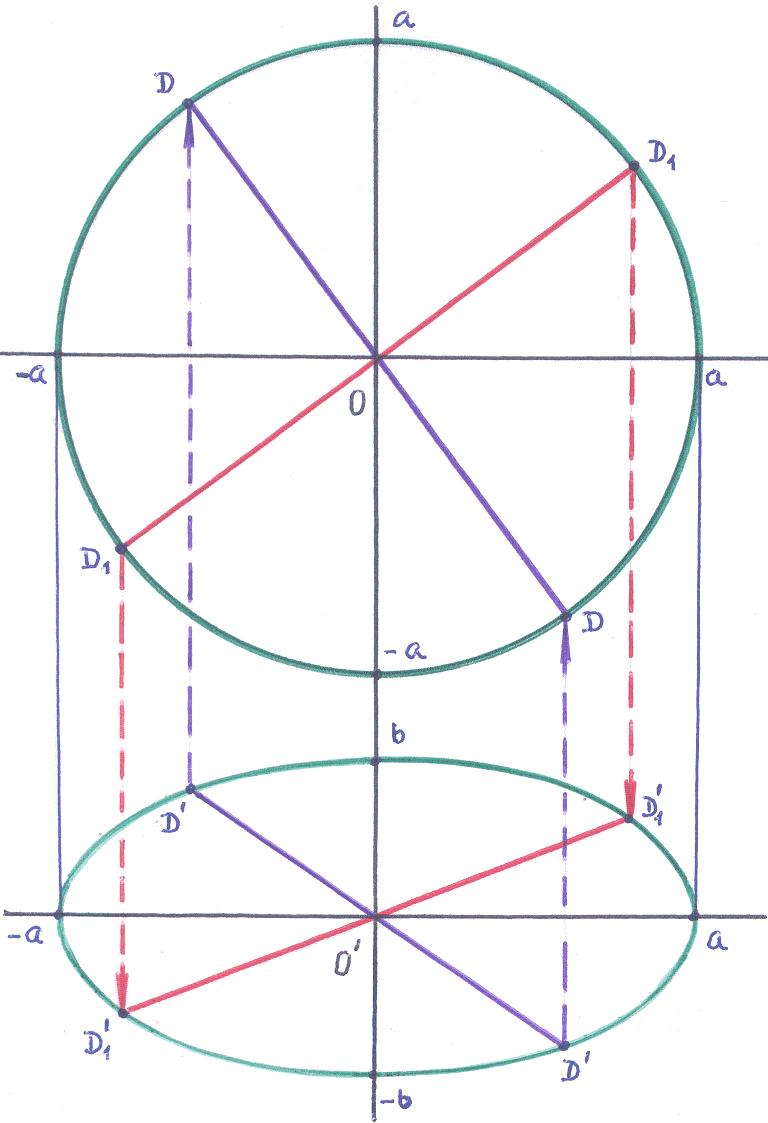ешение:

1). При определении уравнений эллипса рассмотрен геометрический способ построения эллипса. Для нас сейчас важно то, что ортогональное параллельное проектирование превращает окружность в эллипс. Отмечалось также, что это равносильно сжатию окружности с коэффициентом сжатия: =.

2). По условию мы имеем эллипс. Это значит, что мы имеем диаметр окружности: =2. Так как проекция окружности ортогональная, то можем отметить центр окружности: на перпендикуляре, идущем из центра эллипса, и начертить окружность.

3). Отметим на эллипсе один из его диаметров : он проходит через центр эллипса. Нетрудно отметить на окружности диаметр , который является проекцией отмеченного диаметра эллипса.

4). У окружности отметим сопряжённый диаметр : он перпендикулярен диаметру . Отобразим диаметр на эллипс. Получен диаметр , сопряжённый диаметру: . Это и есть проекция перпендикулярного диаметра окружности.

Ответ: указано в тексте и на рисунке.

Замечание: рассмотренный пример интересен тем, что для нахождения сопряжённых диаметров используются только геометрические средства.

Пример 5–12: Дан эллипс: . Найти уравнения двух сопряжённых диаметров этого эллипса, один из которых проходит через точку (4,2).

Решение:

1). Учтём, что все диаметры эллипса проходят через начало координат: . Для диаметра, проходящего через точку , вычисляем: =.

2). Воспользуемся выражением: == = – для угловых коэффициентов сопряжённых диаметров эллипса. Так как =, то необходимо =–1.

3). В таком случае: если один диаметр имеет уравнение =, то другой: =–.

Ответ: один диаметр имеет уравнение =, другой: =–.

Пример 5–13: Составить уравнение хорды эллипса , проходящей через точку (1,-2) и делящейся ею пополам.

Решение:

1). Учтём, что все диаметры эллипса проходят через начало координат: . Для диаметра, проходящего через точку , вычисляем: =–2. Этот диаметр сопряжён искомой хорде.

2). Воспользуемся условием: == –. Это значит, что угловой коэффициент искомой хорды =.

3). Уравнение хорды, проходящей через точку и имеющей угловой коэффициент , можно записать в виде: , или .

Ответ: уравнение хорды: .

Пример 5–14: Составить уравнение диаметра гиперболы для хорды, определяемой прямой .

Решение:

1). Так как хорда имеет направление =2, то сопряжённый ей диаметр имеет угловой коэффициент ==.

2). Так как диаметр гиперболы проходит через начало координат, то его уравнение: =, или .

Ответ: уравнение диаметра: .

Пример 5–15: Составить уравнения сопряжённых диаметров гиперболы , угол между которыми равен .

Решение:

1). Воспользуемся выражением: ==.

2). Так как =1 =, то из системы уравнений: получим два решения: =–, =–3, или =3, =. Так как диаметры проходят через начало координат, пары сопряжённых диаметров: а) =, =–3; б) =3, =.

Ответ: уравнения сопряжённых диаметров: а) =, =–3; б) =3, =.

Пример 5–16: Дана парабола: . Через точку (–1,1) провести такую хорду, которая в этой точке делилась бы пополам.

Решение:

1). Так как хорда проходит через точку , то её уравнение запишем как: .

2). Из уравнения параболы: =–4. Так как точка есть середина хорды, то диаметр должен через неё проходить! Из уравнения диаметра: = получаем: , откуда =–4.

3). Уравнение искомой хорды принимает вид: .

Ответ: уравнение хорды: .

☻

Касательные к кривым второго порядка. Продолжим исследование кривых второго порядка, используя общее для этих кривых уравнение:

. (21)

Из уравнения (21), используя канонические уравнения кривых второго порядка, получаем:

Окружность: при ==1, =0, =–; эллипс: при =, =, =0, =–1.

Гипербола: при =, =–, =0, =–1; парабола: при =0, =1, =– p, =0.

Уравнение (21) неявно может определять либо функцию , либо . Для определения касательной к кривой или кривой можно было бы воспользоваться понятием производной. Мы поступим иначе: воспользуемся определением касательной рассмотрением предельного перехода по отношению к секущей.

Обозначим концы секущей: точки и . Так как точки и принадлежат кривой, то, используя уравнение (20), можем записать:

, .

Вычитая из первого равенства второе, получим выражение:

. (21)

Рассмотрим два случая:

1). Пусть точка не является вершиной линии второго порядка, расположенной на оси , то есть . Учитывая, что угловой коэффициент секущей: =, из равенства (21) получим: =. Предельное положение секущей при неограниченном приближении точки к точке определяется выражением:

==. (22)

2). Пусть теперь точка является вершиной линии второго порядка и располагается на оси . В этом случае =0 и . Разделим равенство (21) на разность: . В этом случае получим: . (23)

Так как для всех кривых второго порядка: , то =0. Это значит, что касательная к линии второго порядка в вершине, лежащей на оси , параллельна оси .

Общие результаты применим для каждой из кривых второго порядка.

Эллипс. Так как для эллипса в общем уравнении: A=, B=, C=0, то выражение для углового коэффициента касательной (22) принимает вид: =–.

Уравнение касательной в точке запишем, используя уравнение :

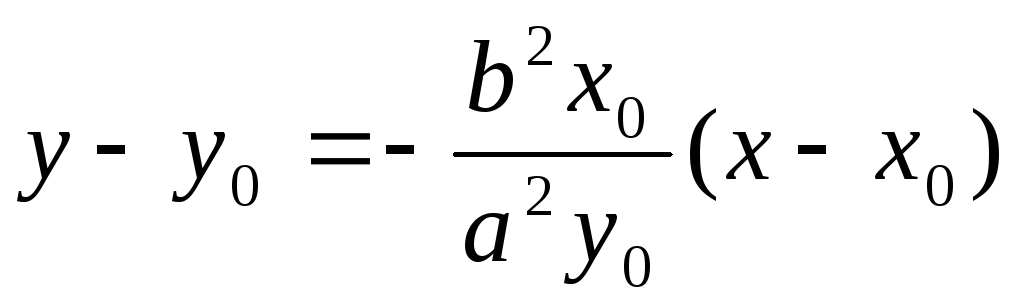или =.

Так как точка принадлежит эллипсу, последнее равенство можно упростить, воспользовавшись тождеством: =1. Окончательно имеем уравнение касательной к эллипсу:

: =1. (24)

Так как окружность есть частный случай эллипса при значениях , то уравнение касательной для окружности имеет вид:

=1. (25)

Свойство касательных эллипса: касательные к эллипсу составляют равные углы с фокальными радиусами, проведёнными в точку касания. Докажем это геометрически изумительное свойство: лучи света, испущенные из одного фокуса эллипса, сбираются (все!) в другом фокусе (пусть линия эллипса идеально отражающая)!

Для доказательства свойства нам потребуется рассмотреть треугольники и , а именно доказать, что они подобны.

Для нахождения отрезков и нормализуем уравнение касательной: , то есть уравнение: или . Для этого (вспомним!) необходимо умножить уравнение на множитель со знаком , если , и со знаком , если . В нашем случае принимаем знак , а величина множителя: . Тогда нормированное уравнение касательной: . Учитывая: и , найдём отклонения этих точек от касательной :

= и =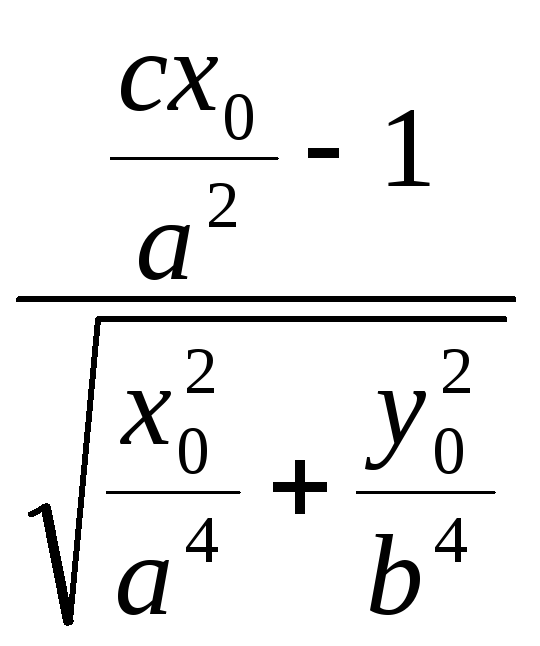, причём: , <0.

Для доказательства подобия треугольников и составим отношение:

===== → треугольники подобны.

Из подобия треугольников и следует равенство углов: и . Свойство доказано.

Если вращать эллипс вокруг его большой оси, то получится эллиптическая поверхность (это подробно рассматривается в Главе 6!). Если сделать эту поверхность изнутри зеркальной, то (вспомним раздел физики – оптику!) лучи, испускаемые источником, помещённым в одном из фокусов, будут собираться в другом фокусе.

☺☺

Пример 5–17: Даны две одинаковые зубчатые шестерни эллиптической формы. Одна из них насажена на ведущий вал (передаёт вращающий момент), а вторая на ведомый (такая конструкция называется редуктором). Вычертить механизм зубчатой передачи и проанализировать кинематику её движения.

Решение:

1). В соответствии с рисунком будем считать, что ведущий вал зубчатого зацепления помещён в фокус нижней шестерёнки, а ведомый вал закреплён в фокусе верхней. Для работы зубчатой передачи необходимо, чтобы расстояние было неизменным. Это значит, что выполняется равенство: =.

2). Из условия: = следует, что отрезки и принадлежат одной прямой. Тогда = и =. Из этого следует, что одновременно: = и отрезки и также принадлежат одной прямой.

3). Из полученных в пункте 2) результатов имеем: прямая есть общая касательная находящихся в зацеплении шестерёнок.

4). Теперь не представляет большого труда вычертить механизм зубчатого зацепления. Вычерчивание верхнего эллипса (шестерёнки) выполняем сжатием окружности радиуса . На нижней дуге эллипса выбираем точку : произвольно, но не посередине дуги (для красоты!). На прямой: , отмечаем точку . Аналогично строим точку . Середина отрезка определяет центр нижнего эллипса (и вспомогательной окружности!). Вычерчиваем нижний эллипс. Рисунок готов!

5). Учтём, что вектор скорости точки направлен по общей касательной эллипсов, а плечи этого вектора относительно оси вращения и относительно оси вращения постоянно изменяются. Это значит, что при постоянной угловой скорости ведущей шестерёнки ведомая шестерёнка будет вращаться с переменной угловой скоростью. Это свойство редуктора с эллиптическими шестерёнками используют в конструкциях разных станков, например строгальных!

Ответ: в тексте обосновано построение чертежа и проанализированы кинематические особенности эллиптического зубчатого зацепления (редуктора).

☻

Найдём условия того, что прямая : касается эллипса , то есть совпадает с касательной эллипса : = в точке .

Известно, что две прямые и совпадают, если ==. В нашем случае это условие принимает вид: , откуда = и =. Так как точка принадлежит , то выполняется равенство: , или:

. (26)

Итак, мы имеем необходимое условие (26) касания заданной прямой заданного эллипса. Будет ли это условие достаточным? Пусть условие (26) выполняется. Перепишем его в виде:

.

Последнее означает, что точка: =, = принадлежит эллипсу. Подставим координаты точки в уравнение касательной эллипса, то есть в уравнение: =0. Получаем: . Это значит, если условие (26) выполняется, то прямая есть касательная эллипса. Таким образом, условие (26) есть необходимое и достаточное условие того, что касается эллипса.

☺☺

Пример 5–18: Найти уравнения касательных к эллипсу , параллельных прямой :. Найти расстояние между касательными.

Решение:

1). Уравнение касательной должно иметь вид : =, причём за счёт выбора соответствующего значения параметра можно добиться совпадения: =. Если воспользоваться условием (26): , то для данного примера получим равенство: , откуда значение параметра =24.

2). Как и следовало ожидать (из геометрических соображений!), у эллипса нашлось две касательные, параллельные заданному направлению. Одна : и вторая : .

3). Найдём расстояние от точки (0,0) до касательной . Для этого воспользуемся отклонением: =. Из этого следует: =. Расстояние между касательными равно 2= .

Ответ: касательные : и : , расстояние 2=.

Замечание: рассмотренный пример можно было решить традиционным способом: найти производную неявно заданной функции и, приравняв её заданному прямой угловому коэффициенту, из полученного равенства вычислить координаты точки касания ; затем из условия принадлежности касательной вычислить параметр ! Здорово?

☻

Гипербола. Так как для гиперболы в общем уравнении: A=, B=–, C=0, то выражение для углового коэффициента касательной (22) принимает вид: =.

Уравнение касательной в точке запишем, используя уравнение :

или =.

Уравнение касательной в точке запишем, используя уравнение :

Так как точка принадлежит гиперболе, последнее равенство можно упростить, воспользовавшись тождеством: =1. Окончательно имеем уравнение касательной к гиперболе: : =1. (27)

Свойство касательных гиперболы: касательные к гиперболе составляют равные углы с фокальными радиусами, проведёнными в точку касания.

Для доказательства свойства нам потребуется рассмотреть треугольники и , а именно доказать, что они подобны.

Для нахождения отрезков и нормализуем уравнение касательной: , то есть уравнение: или . Для этого (вспомним!) необходимо умножить уравнение на множитель со знаком , если , и со знаком , если . В нашем случае принимаем знак , а величина множителя: . Тогда нормированное уравнение касательной: . Учитывая: и , найдём отклонения этих точек от касательной :

= и =, причём: .

Условие: отражает тот факт, что фокусы гиперболы располагаются по разные стороны касательной, то есть находятся в разных полуплоскостях.

Докажем подобие треугольников и для случая, когда точка принадлежит правой ветви гиперболы (используем симметрию кривой!). Тогда можем записать:

===== → треугольники подобны.

Из подобия треугольников и следует равенство углов: и . Свойство доказано.

Если вращать гиперболу вокруг её действительной оси, то получится гиперболическая поверхность – гиперболоид (это подробно рассматривается в Главе 6!). Если сделать эту поверхность изнутри зеркальной, то (вспомним раздел физики – оптику!) лучи, испускаемые источником, помещённым в одном из фокусов, будем наблюдать так (по направлению ), будто их излучает другой фокус (мнимое изображение первого фокуса!). Имеет место расходящийся пучок лучей!

Замечание: полученный для гиперболоида результат превращает грозное оружие инженера Гарина – гиперболоид инженера Гарина в безобидную игрушку!

Найдём условия того, что прямая : касается гиперболы , то есть совпадает с касательной гиперболы : = в точке .

Известно, что две прямые и совпадают, если ==. В нашем случае это условие принимает вид: , откуда = и =. Так как точка принадлежит , то выполняется равенство: , или:

. (27)

Итак, мы имеем необходимое условие (27) касания заданной прямой заданной гиперболы. Будет ли это условие достаточным? Пусть условие (27) выполняется. Перепишем его в виде:

.

Последнее означает, что точка: =, = принадлежит гиперболе. Подставим координаты точки в уравнение касательной гиперболы, то есть в уравнение: =0. Получаем: . Это значит, если условие (27) выполняется, то прямая есть касательная гиперболы. Таким образом, условие (27) есть необходимое и достаточное условие того, что касается гиперболы.

Замечание: легко заметить, что условие (27) невозможно, если ; этому условию геометрически соответствуют все случаи, когда угловой коэффициент прямой попадает в диапазон, определяемый асимптотами гиперболы: .

☺☺

Пример 5–19: Найти уравнения касательных к гиперболе , параллельных прямой : .

Решение:

1). Уравнение касательной должно иметь вид : =, причём за счёт выбора соответствующего значения параметра можно добиться совпадения прямой с касательной . Проверим выполнимость условия (27): . Угловой коэффициент прямой равен > → касательная существует, и условие (27) выполняется.

2). Воспользуемся условием: . В данном примере: =. Значение параметра =32.

3). Как и следовало ожидать (из геометрических соображений!), у гиперболы нашлось две касательные, параллельные заданному направлению. Одна : и вторая : .

Ответ: касательные одна : и вторая : .

Замечание: важно не пропустить проверку углового коэффициента прямой : возможно не потребуется находить касательную!

☻

Парабола. Так как для гиперболы в общем уравнении: A=0, B=1, C=–p, то выражение для углового коэффициента касательной (22) принимает вид: =.

Уравнение касательной в точке запишем, используя уравнение :

или .

Так как точка принадлежит параболе, последнее равенство можно упростить, воспользовавшись тождеством: . Окончательно имеем уравнение касательной к параболе : , или . (28)

Свойство касательных параболы: касательные к параболе составляют равные углы с фокальным радиусом параболы и прямой, параллельной оси параболы, и проходящей через точку касания параболы. В соответствии с рисунком это значит, что угол равен углу между касательной и прямой , параллельной оси .

Для доказательства свойства нам потребуется рассмотреть треугольник и доказать, что он равнобедренный.

Обозначим: . Учитывая уравнение касательной (28) получаем: =–. В то же время у параболы: =+. Вычислим также: =+=+. Доказано, что треугольник равнобедренный. Из этого следует, что угол ==. Но углы и равны как углы с параллельными сторонами. Из этого следует равенство углов ==. Свойство доказано!

Найдём условия того, что прямая : касается параболы , то есть совпадает с касательной параболы : = в точке .

Известно, что две прямые и совпадают, если ==. В нашем случае это условие принимает вид: , откуда = и =. Так как точка принадлежит , то выполняется равенство: , или:

. (29)

Итак, мы имеем необходимое условие (29) касания заданной прямой заданной параболы. Будет ли это условие достаточным? Пусть условие (29) выполняется. Перепишем его в виде: .

Последнее означает, что точка: =, = принадлежит параболе. Подставим координаты точки в уравнение касательной параболы, то есть в уравнение: . Получаем: , или. Это значит, если условие (29) выполняется, то прямая есть касательная гиперболы. Таким образом, условие (29) есть необходимое и достаточное условие того, что касается гиперболы.

Замечание: легко заметить, что условие (29) невозможно при значении , если и имеют разные знаки; это геометрически невозможно, когда парабола расположена справа от оси , а точка касания оказалась слева от неё.

Отметим оптические свойства параболы: лучи света, исходящие из фокуса параболы, после зеркального отражения от параболы образуют пучок, параллельный оси параболы (это учитывают при создании прожекторов и теле- и радиоантенн)!

Замечание: Это значит, что у инженера Гарина был не гиперболоид (как пошутил Алексей Толстой), а параболоид!

☺☺

Пример 5–20: Найти уравнение касательной к параболе , параллельной прямой : .

Решение:

1). Уравнение касательной должно иметь вид : , или , причём за счёт выбора соответствующего значения параметра можно добиться совпадения прямой с касательной .

2). Воспользуемся условием: . В данном примере: . Значение параметра =4. Знаки и совпадают!

3). Как и следовало ожидать (из геометрических соображений!), у параболы одна касательная, параллельная заданному направлению. Одна : .

Ответ: касательная одна : , или .

Рассмотрим несколько примеров, в которых обобщается использование свойств кривых второго порядка.

☻

Пример 5–21: Составить уравнение касательной к эллипсу: , перпендикулярной прямой :.

Решение:

1). Имея , легко записать уравнение касательной эллипса, перпендикулярной , в виде : =, причём за счёт выбора соответствующего значения параметра можно добиться совпадения: =. Если воспользоваться условием (26): , то для данного примера получим равенство: , откуда значение параметра =10.

2). Запишем уравнения касательных, перпендикулярных заданному направлению. Одна : и вторая : .

Ответ: касательные : и : .

Пример 5–22: На эллипсе: найти точку , ближайшую к прямой : и вычислить расстояние от точки M₀ до этой прямой.

Решение:

1). Учтём свойство эллипса по отношению к его касательным: его верхняя половина располагается под касательной, а нижняя над касательной. Заметим также, что рисунок не отражает окончательные результаты решения задачи: взаимное расположение всех геометрических фигур на самом деле может оказаться другим. Рисунок мы рассматриваем как эскиз образа исходных данных задачи.

2). Так как касательные: и должны быть параллельны прямой , то общим уравнением для них может быть запись: =, причём за счёт выбора соответствующего значения параметра можно добиться совпадения: с и . Если воспользоваться условием (26): , то для данного примера получим равенство: , откуда значение параметра =24. Для верхней касательной имеем :, или , для нижней касательной, соответственно : .

3). Полученные результаты позволяют уточнить взаимное расположение , , и эллипса. Так как прямая пересекает ось в точке (0; 11.5), то ближе к прямой располагается множество точек касательной . Так как прямая пересекает ось в точке (0; 12), то она располагается выше прямой . Точка определяется из полученных ранее выражений с учётом окончательной записи : ===–5, ===2.

4). Нормализуя заданное уравнение, получаем :. Для нахождения расстояния между параллельными прямыми: и воспользуемся точкой (0,12), принадлежащей , а не точкой . Для выделенной точки отклонение от : ==–.

5). Тогда можем записать: ==.

Ответ: точка: (–5,2); расстояние: =.

Пример 5–23: На гиперболе: найти точку , ближайшую к прямой : и вычислить расстояние от точки до этой прямой.

Решение:

1). Учтём свойство гиперболы по отношению к её касательным: её верхняя половина располагается под касательной, а нижняя над касательной. Заметим также, что рисунок не отражает окончательные результаты решения задачи: взаимное расположение всех геометрических фигур на самом деле может оказаться другим. Рисунок мы рассматриваем как эскиз образа исходных данных задачи.

2). Из условия следует, что угловые коэффициенты асимптот гиперболы: k=. Угловой коэффициент прямой равен =. Проверим выполнимость условия (27): . Угловой коэффициент прямой равен > → касательная существует, и условие (27) выполняется.

3). Так как касательные: и должны быть параллельны прямой , то общим уравнением для них может быть запись: =, причём за счёт выбора соответствующего значения параметра можно добиться совпадения: с и . Воспользуемся условием: . В данном примере: =. Значение параметра =12. Это значит :, : .

4). Так как прямая пересекает ось в точке , ближе к ней располагается прямая . Это значит, по условию задачи нам нужна точка . Вычислим её координаты: ===–6, ===3.

5). Нормализуя заданное уравнение, получаем :=0. Для нахождения расстояния между параллельными прямыми: и воспользуемся точкой (–4,0), принадлежащей , а не точкой . Для выделенной точки отклонение от : =, или =–.

6). Тогда можем записать: ==.

Ответ: точка: (–6,3); расстояние: =.

Пример 5–24: На параболе: найти точку , ближайшую к прямой и вычислить расстояние от точки до этой прямой.

Решение:

1). Учтём свойство параболы по отношению к её касательным: её верхняя половина располагается под касательной, а нижняя над касательной. Заметим также, что рисунок не отражает окончательные результаты решения задачи: взаимное расположение всех геометрических фигур на самом деле может оказаться другим. Рисунок мы рассматриваем как эскиз образа исходных данных задачи. Понятно, что точка должна лежать на касательной гиперболы, параллельной заданной прямой.

2). Из условия следует, что угловой коэффициент касательной должен быть: =–. Это значит, что точка касания располагается на нижней ветви параболы.

3). Уравнение касательной должно иметь вид : , или , причём за счёт выбора соответствующего значения параметра можно добиться совпадения прямой с касательной .

4). Воспользуемся условием: . В данном примере: . Значение параметра =36. Тогда уравнение касательной :

4). Вычислим координаты точки касания: ===9 и ===–24.

5). Нормализуя заданное уравнение, получаем :=0. Для нахождения расстояния между параллельными прямыми: и воспользуемся точкой (–9,0), принадлежащей , а не точкой . Для выделенной точки отклонение от : ==–10.

6). Тогда можем записать: ==10.

Ответ: точка: (9,–24); расстояние: =10.

☻