187 Аг: Глава 5-1

Глава 5. Кривые второго порядка. Приведение общего уравнения кривой второго порядка к каноническому виду.

При изучении векторов, прямых и отрезков прямых, прежде всего, использовалось двумерное пространство. Только после получения достаточного количества результатов и наработки определённого опыта их использования в этом пространстве мы перешли в трёхмерное пространство.

В случае кривых второго порядка такая последовательность использования пространств тем более оправдана. Это определяется не только сложностью объекта изучения, но и тем, что в элементарной геометрии (то есть в школе) используется только окружность, причём без исследования её аналитических свойств.

Отметим также, что все кривые (плоские кривые!) мы будем рассматривать как множество точек, обладающих некоторым общим свойством. Именно назначенное свойство точек будет определять исходное аналитическое выражение кривой.

Заметим также, что после получения аналитического выражения (уравнения) кривой применяются средства математического анализа и аналитической геометрии для исследования свойств полученной кривой. В этом смысле возможности аналитической геометрии должны проявиться ещё более выразительно и эффективно.

Чем вызван интерес к кривым второго порядка? – Прежде всего, тем, что они широко применяются в инженерной практике: кривые второго порядка технологичны. Кроме того, эти кривые часто проявляются в физике. Так материальная точка в поле тяготения Земли, в общем случае, движется по параболе. Спутник некоторой планеты, независимо от истории его происхождения, движется по эллиптической орбите. Много других примеров!..

Важно и то, что аналитические модели указанных фигур достаточно просты, и оптимизационные задачи при построении различных технических конструкций с использованием кривых второго порядка решаются достаточно просто.

§ 1. Кривые второго порядка: окружность, эллипс, гипербола, парабола.

Известно, что линиями первого порядка на плоскости являются прямые. Алгебраически, в общем случае, эти линии представляются в виде выражения: , где – параметры, – переменные.

Линии второго порядка, в общем случае, представляются в виде выражения:

. (1)

Мы увидим, что выражение (1) определяет (в зависимости от конкретного набора коэффициентов ) кривые второго порядка: окружность, эллипс, гиперболу, параболу или пару прямых. Прежде, чем рассматривать общую запись (1), изучим отдельно названные кривые по их простейшим алгебраическим выражениям, основанным на определенных (простейших) их свойствах.

Окружность: геометрическое место точек плоскости, равноудаленных от заданной точки плоскости, называемой центром окружности, Расстояние от точки окружности до её центра называется радиусом окружности. Радиусом называют также любой отрезок, соединяющий точку окружности с её центром.

Следует отметить, что уточнение определения окружности: радиусом называют также любой отрезок, соединяющий точку окружности с её центром, очень важно! Это значит, что для выделения на плоскости точек окружности не обязательно применять циркуль.

Для выделения на плоскости произвольной точки окружности достаточно провести из центра окружности луч и отложить на этом луче от точки отрезок длиной – радиус. Именно такое толкование окружности (не как линии, а как множества точек плоскости) применим для получения аналитической модели (уравнения) окружности.

Пусть точка – произвольная точка плоскости. Из определения окружности следует, что точка будет принадлежать окружности только в том случае, если отрезок есть радиус окружности, то есть: =. Запишем вектор: = Используя определение длины отрезка , можем записать: , или в виде:

→ нормальное уравнение. (2)

Если центр окружности находится в начале координат (0,0), то уравнение (2) принимает простейший вид:

→ каноническое уравнение. (3)

Пусть выражение (1) имеет частный вид (коэффициенты при квадратах переменных одинаковы!): . Из этого уравнения (используя тождественное преобразование: выделение полного квадрата) нетрудно получить выражение:

.

Так как все участвующие в записи общего вида параметры произвольные числа, то число может принимать произвольные значения. В зависимости от величины Е могут реализоваться такие случаи:

1). > 0 , то есть → окружность: .

2). = 0 → , выполняется для одной точки (x₀,y₀) .

3). < 0 , то есть → – мнимая окружность.

☺☺

Пример 5–01: Доказать, что заданием трёх точек, не лежащих на одной прямой, окружность определяется однозначно, то есть однозначно определяются параметры уравнения (3).

Решение:

1). Задача равносильна задаче о нахождении окружности, описанной около треугольника.

2). Известно, что через одну точку можно провести бесчисленное множество окружностей. Для этого достаточно из точки в любом направлении провести луч, отметить на нем произвольную точку и радиусом = определить окружность:

.

3). В элементарной геометрии показано, что через две точки и можно провести бесчисленное множество окружностей. Для этого достаточно построить к отрезку срединный перпендикуляр, отметить на нём произвольную точку и радиусом = определить окружность: .

4). Если заданы три точки , и , не лежащие на одной прямой, то они определяют только одну окружность. Для этого достаточно вспомнить способ построения описанной около треугольника окружности: это пересечение срединных перпендикуляров сторон треугольника: точка пересечения единственна, вычисление радиуса не представляет труда: =, где – стороны треугольника, – площадь треугольника.

5). Используя результаты элементарной геометрии, можем утверждать, что три точки, не лежащие на одной прямой, определяют окружность однозначно.

Ответ: доказано: три точки, не лежащие на одной прямой, определяют окружность однозначно.

Пример 5–02: Заданы три точки: (1,0), (0,1), (1,2). Найти уравнение окружности, проходящей через три заданные точки.

Решение:

1). Так как точки ,, не лежат на одной прямой (легко проверить!), то окружность существует и единственна. Из условия принадлежности точек окружности запишем:

: , :, :.

2). Вычитая из уравнения уравнение и из уравнения уравнение , получим два нелинейных уравнения для неизвестных параметров . В элементарной алгебре этот тип систем достаточно подробно изучается! В нашем случае имеем:

– → =1, – → =1.

3). Подставляя полученные значения параметров и в уравнение , получаем =1. Остаётся записать уравнение окружности: .

Замечание: рассмотренный пример прост, но схему вычислений параметров отражает достаточно полно и поможет решать задачу в самом общем случае.

Ответ: уравнение окружности: .

☻

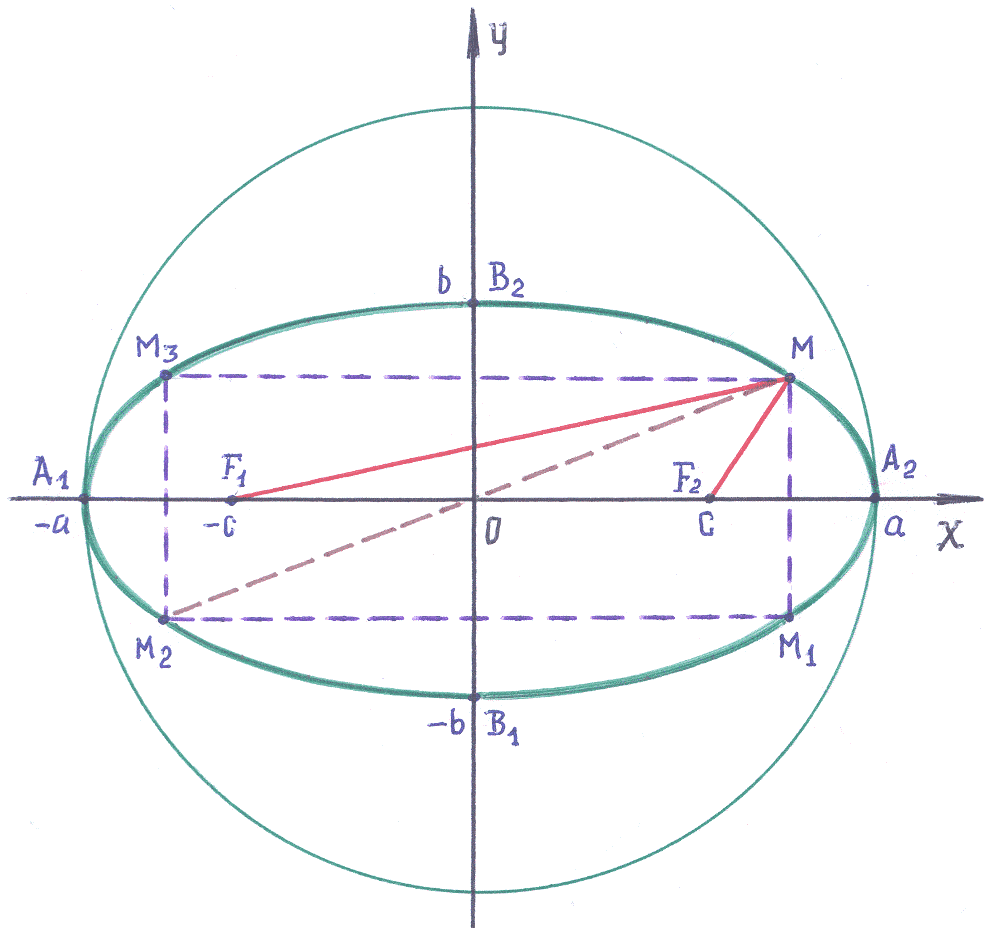
Эллипс: геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Если произвольную точку плоскости обозначить , то множество точек эллипс состоит только из точек, наделённых особым совокупным свойст­вом трёх точек, две из которых неподвижны, а третья – переменная.

Принимая обозначения участвующих в определении величин в соответствии с рисунком, обратим внимание на условие: +=2>2. Для треугольника записанное неравенство есть неравенство треугольника. При условии +=2 треугольник превращается в отрезок , а множество точек эллипс есть этот же отрезок.

Отметим также особенность записи: +=2. Коэффициент 2 принят только, исходя из удобства алгебраических преобразований и записи конечных выражений! Для дальнейшего применения введём также обозначение : далее проявится геометрический смысл этого выражения.

Используя выражение для вычисления длины отрезка, запишем длины отрезков и : =, =.

По определению эллипса получаем алгебраическое свойство множества точек, составляющих эллипс:

. (4)

Так как предполагается получить уравнения нескольких (разных!) кривых 2-го порядка, то будет полезным детально следовать по шагам преобразований аксиоматического (то есть, по определению!) выражения (4).

Прежде всего, изолируем один из корней в выражении (4) и возведём полученное равенство в квадрат (преобразование, не являющееся тождественным):

,

откуда получаем: . (5)

Последнее ещё раз возводим в квадрат и применяем тождественные преобразования к полученному равенству:

, или , (6)

При условии, что > . Применение этого условия показывает, что: . Это значит, что обозначение: непротиворечиво! Разделив равенство (5) на , получаем уравнение: – каноническое уравнение эллипса. (7)

Используя выражения (5) и (4), применяя обозначение: , запишем соотношения для вычисления расстояний и :

=, =, (8)

параметр эллипса – эксцентриситет. Учитывая: >, заметим, что .

Заметим, что переход от выражения (4) к выражению (7) осуществлён с нарушением тождественности преобразований: дважды применялось возведение в квадрат! Это требует дополнительного исследования уравнения (7): не случилось ли так, что кроме точек удовлетворяющих свойству (4), выражение (7) удовлетворяется ещё какими-то точками.

Пусть имеется точка , удовлетворяющая (7). Это значит, что верно:

→ проверим: +=+=2.

Вычислим: ===. Так как =, то получаем верное выражение: =. Аналогично получаем верное выражение: =. Это значит, точка , удовлетворяющая уравнению (7) принадлежит множеству точек эллипс! Доказано: условие (4) и уравнение (7) выделяют на плоскости только точки, принадлежащие эллипсу!

Принятое в определении эллипса свойство входящих в него точек позволяет нарисовать линию-эллипс, не имея уравнения для эллипса!

Придумка: Эллипс можно начертить, используя простейшие приспособления. Пусть решили начертить эллипс на полянке в лесу. Забиваем в точках F₁ и F₂ колышки, закрепляем на них концы шнура, длина которого больше отрезка F₁F₂. Натягиваем шнур (обе ветви r₁,r₂ натянуты), взявшись за его произвольную точку М, и забиваем колышек в вершине угла F₁МF₂. Если точу М смещать вдоль шнура и для каждого её нового положения (обе ветви r₁,r₂ натянуты) забивать колышек, на полянке появится чертёж правильного эллипса!

Имея определяющее эллипс уравнение (7), можно, используя средства математического анализа, приступить к исследованию свойств эллипса (для удобства наблюдения исследуемых свойств имеем подробный рисунок эллипса и его элементов!):

1). Первое, что легко выделяется из уравнения: и . Точки ,,, называют вершинами эллипса. Отрезок оси – большая ось эллипса; отрезок оси – малая ось эллипса.

2). График кривой симметричен относительно осей , и начала координат: это определяется чётностью степеней при переменных в уравнении (7).

3). Рассмотрим частные случаи эллипса, определяемого уравнением (7). Если =, то уравнение (7) превращается в уравнение для окружности: . В таком случае =0 и эксцентриситет: =0.

Если =0, то =. Так как делить на 0 нельзя, то возвращаемся к промежуточному выражению: , из которого получаем только =0. В этом случае множество точек эллипс превращается в отрезок . Это не допускается по определению эллипса, как отмечалось раньше.

4). Эллипс – результат параллельного ортогонального проектирования.

Результат параллельного проектирования окружности легко наблюдается вокруг нас: стоит лишь заняться рассматриванием круга под разными углами зрения (вращая круг вокруг его диаметра). Цилиндр при рассматривании его сбоку – всего лишь прямоугольник. А если посмотреть на него сверху? Теперь видим круг. А если захочется рассматривать цилиндр так, чтобы видеть и боковую поверхность и одно из оснований? Теперь всё исказилось! – так мы называем в наших ощущениях наблюдаемую картинку. В геометрии это явление определяют как результат проектирования геометрической фигуры на некоторую плоскость.

Когда говорится о параллельном ортогональном проектировании, то имеют в виду два условия:

а) геометрическая фигура проектируется на плоскость, а не на произвольную поверхность;

б) из каждой точки геометрической фигуры на плоскость проектирования опускается перпендикуляр (известно, что все они параллельны): его основание отмечает точку-проекцию исходной фигуры.

Из рисунка нетрудно заметить связь координат точек исходной геометрической фигуры (она расположена в плоскости в системе координат ) и координат фигуры-проекции (расположена в плоскости в системе координат ):

→ . (9)

Если применить преобразование (9) к геометрической фигуре окружность, то легко заметить, что в результате такого преобразования получаем эллипс:

окружность: → , или – эллипс. (10)

Построение эллипса при помощи чертёжных приборов

5). Эллипс – результат сжатия окружности: . Наблюдение результата ортогонального параллельного проектирования подсказывает практический способ построения эллипса с заданными параметрами и , то есть с заданными осями:

Пусть требуется построить эллипс с заданными параметрами и . Для построения такого эллипса выполняет следующие действия:

а) строим окружность радиуса в прямоугольной системе координат;

б) принимаем коэффициент сжатия окружности =;

в) применяем коэффициент сжатия к ординатам произвольных точек, не меняя их абсцисс: → реализуем процесс, показанный в преобразовании (10).

☺☺

Пример 5–03: Пусть требуется построить эллипс с заданными параметрами =4 и =2.

Решение:

а) строим окружность радиуса =4 с центром в начале прямоугольной системы координат ;

б) принимаем коэффициент сжатия окружности ==;

в) далее применяем линейку и прямоугольный треугольник: двигаем треугольник вдоль линейки так, чтобы деление [4] всё время оставалось на оси ;

г) используем ординаты: 1; 2; 3; 4 точек окружности и, двигая треугольник вдоль линейки, отмечаем на плоскости точки с ординатами: ; 1; ; 2;

д) в результате выполнения построений по пункту г) для каждой четверти эллипса получаем по пять точек, которые легко соединить при помощи лекала: эллипс (симпатичный!) построен.

Замечание: значения параметров =4 и =2 и ординат: 1; 2; 3; 4 выбраны так, чтобы каждый раз легко видеть середины выделяемых отрезков.

Ответ: эллипс: – построен.

☻

5). Эллипс – результат сжатия окружности: . Наблюдение результата ортогонального параллельного проектирования подсказывает практический способ построения эллипса с заданными параметрами и , то есть с заданными осями:

6). Параметрические уравнения эллипса. Имея опыт построения параметрических уравнений прямой, напрашивается вопрос: не будет ли это связано с некоторым движением точки на плоскости в системе координат ?

Наиболее удобной моделью для получения параметрических уравнений эллипса считают отрезок , который скользит своими концами и по осям и , соответственно.

При движении отрезка точка (на отрезке закреплена), принадлежащая отрезку, описывает некоторую линию. Найдём её уравнение, введя параметр – угол отрезка с осью координат . Для этого достаточно записать значения координат точки :

(11)

Утверждать, что уравнения (11) есть эллипс, можно только после того, как убедимся, что точка принадлежит уже известному нам уравнению эллипса: .

Подставим координаты точки в каноническое уравнение эллипса:

→ – тождество!

Итак, уравнения (11) представляют эллипс, а именно его параметрические уравнения. Применяя отрезки , отражающие конкретные значения параметров и , можно получить траектории движения точки в зависимости от значения параметра . Если параметр есть время, то получаем закон движения точки по эллиптической орбите.

Неожиданный результат получается, если точку размещать на продолжении отрезка , сохраняя кинематику движения отрезка: отрезок скользит своими концами и по осям и , соответственно. Какую траекторию описывает точка в этом случае?

Найдём уравнение движения точки , используя параметр – угол отрезка с осью координат . Для этого достаточно записать значения координат точки :

(11)

Положив ==, получаем параметрические уравнения, совпадающие с уравнениями (10).

Итак, уравнения (11) представляют эллипс, а именно его параметрические уравнения. Меняя положение точки на прямой , можно получить эллипс с заданными полуосями, причём =, =.

Если точку сделать рисующей, то полученное устройство можно назвать эллиптическим циркулем.

Используя обратимость действия эллиптического циркуля, Леонардо да Винчи предложил кинематическую схему токарного станка для обтачивания валов, имеющих в поперечном сечении эллипс.

Конструкция указанного станка обеспечивает неподвижность точек , а крестовина вместе с прикреплённым к ней патроном приводится в движение. В этом случае деталь, закреплённая в патроне, обтачивается резцом, закреплённым в точке , по эллипсу.

Применяют и другие механизмы, преобразующие криволинейное движение в прямолинейное. Пусть точка движется по прямой , а точка движется по траектории, определяемой заданным эллипсом. В таком случае точка будет двигаться по прямой .

Механизмы, осуществляющие преобразование эллиптического движения в прямолинейное, называют эллиптическими коромыслами. Такие механизмы применяют в строгальных и шлифовальных станках.

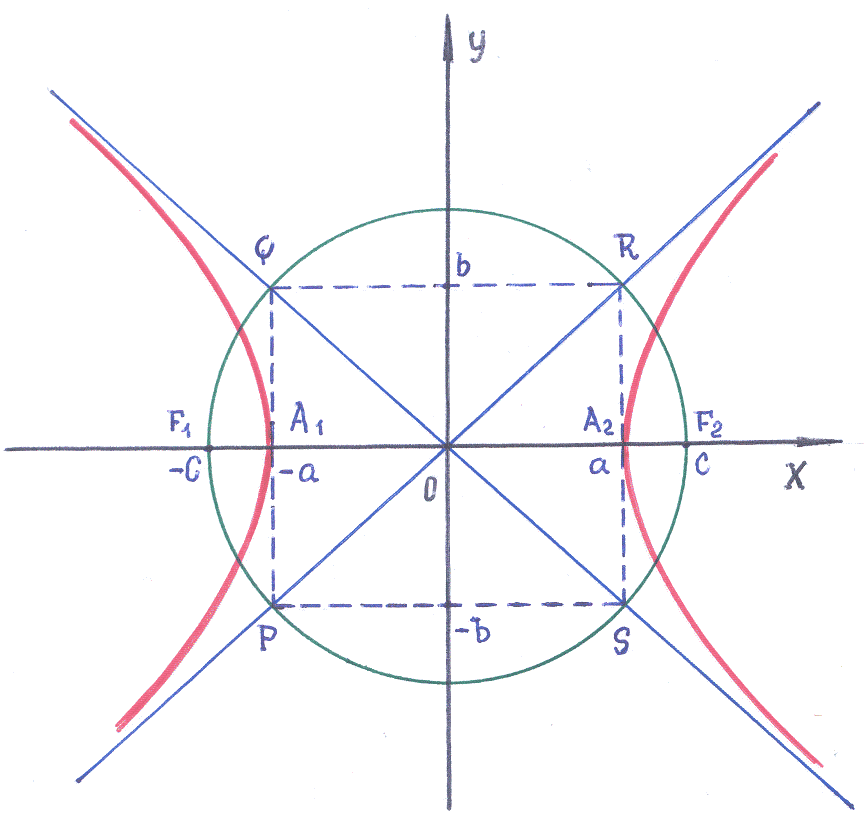
Гипербола: геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами:

Принимая обозначения участвующих в определении величин в соответствии с рисунком, обратим внимание на условие: |–|<2. Для треугольника записанное неравенство есть неравенство треугольника: каждая сторона треугольника больше разности двух других сторон.

Выделим некоторые частные случаи значений параметра . При условии |–|=2 множество точек гиперболы содержит только точки оси : . Если |–|=0, то треугольник становится равнобедренным и множество точек гиперболы – это числовая ось , то есть прямая.

Для удобства примем: |–|=2, причём из определения следует: <. Коэффициент 2 принят только, исходя из удобства алгебраических преобразований и записи конечных выражений! Для дальнейшего применения введём также обозначение : далее проявится геометрический смысл этого выражения.

Используя известные выражения для расстояний и , в соответствии с определением гиперболы запишем:

. (12)

Изолируем один из корней в выражении (12) и возведём полученное равенство в квадрат:

,

откуда получаем: . (13)

Последнее ещё раз возводим в квадрат и применяем тождественные преобразования к полученному равенству:

, или , (14)

При условии, что < . Применение этого условия показывает, что: . Это значит, что обозначение: непротиворечиво! Разделив равенство (14) на , получаем уравнение: – каноническое уравнение гиперболы. (15)

Используя выражения (13) и (12), применяя обозначение: >1, запишем соотношения для вычисления расстояний и : =, =, (16)

параметр гиперболы – эксцентриситет.

Из уравнения (15) следует, что . Это значит, что на интервале нет точек гиперболы. Если , реализуется левая ветвь гиперболы. Если , реализуется правая ветвь гиперболы. Учитывая, что ,>0, рассмотрим возможные случаи:

I. Для значений: получаем: – левая ветвь → (–) =–2.

II. Для значений: получаем: – правая ветвь → (–) =2.

Так как уравнение (15) было получено с нарушением тождественности преобразований: дважды применялось возведение в квадрат, то требуется дополнительного исследования уравнения (15). Пусть имеется точка , удовлетворяющая (15). Это значит, что верно:

→ проверим: =|–|=2.

Вычислим : ===. Это значит, что =, что соответствует записи для левой и правой ветвей гиперболы. Аналогично получаем верное выражение для расстояния =, что соответствует записи для левой и правой ветвей гиперболы. Это значит, точка , удовлетворяющая уравнению (15), принадлежит множеству точек гипербола! Доказано: условие (12) и уравнение (15) выделяют на плоскости только точки, принадлежащие гиперболе!

Принятое в определении гиперболы свойство входящих в него точек позволяет нарисовать линию-гиперболу, не имея уравнения для гиперболы!

Придумка: Гиперболу можно начертить, используя простейшие приспособления. Пусть решили начертить гиперболу на песчаном берегу озера. Забиваем в точках (фокусах) F₁ и F₂ колышки, закрепляем на них концы шнура, произвольной длины, причём на шнуре отмечается точка P такая, что разность длин PF₁ и PF₂ равна заданной величине 2a, меньшей, чем расстояние F₁F₂. Пусть шнур используется по схеме, изображённой на рисунке F₁ M P M F₂. Пусть Вася удерживает шнур за точку P, а Петя, имея в точке М перпендикулярный к песчаной поверхности штырь, рисует на песке непрерывную линию (обе ветви F₁M, F₂M натянуты). Эта линия будет гиперболой!

Имея определяющее гиперболу уравнение (15), можно, используя средства математического анализа, приступить к исследованию свойств гиперболы (для удобства наблюдения исследуемых свойств имеем подробный рисунок гиперболы и её элементов!):

1). Первое, что легко выделяется из уравнения гиперболы: область определения и область значений: . Точки , называют вершинами гиперболы. Ось – действительная ось гиперболы, ось – мнимая ось гиперболы.

2). График кривой симметричен относительно осей , и начала координат: это определяется чётностью степеней при переменных в уравнении (15).

3). Если задано уравнение гиперболы, то определены параметры: и . Используя циркуль, легко отмечают на оси точки фокусов гиперболы.

4). Гипербола имеет асимптоты: ==. В математическом анализе показано, что для нахождения асимптот необходимо вычислить пределы:

;

.

Построение графика гиперболы не представляет особого труда: учитывая симметрию графика относительно осей координат, достаточно построить только четверть кривой в первой четверти плоскости . На рисунке легко прочитываются все затронутые свойства гиперболы:

Парабола: геометрическое место точек плоскости, для каждой из которых расстояние до данной точки плоскости, называемой фокусом, равно расстоянию до данной прямой, называемой директрисой.

В соответствии с определением параболы, отметим на плоскости точку – фокус и прямую – директрису:

Используя принятые на рисунке обозначения, запишем в соответствии принятым определением параболы: → → . (17)

Получено простейшее уравнение параболы:

→ каноническое уравнение параболы. (18)

Определяющее свойство параболы равносильно свойству: – эксцентриситет параболы.

Принятое в определении параболы свойство входящих в него точек позволяет нарисовать линию-параболу, не имея уравнения для параболы!

Придумка: Параболу можно начертить, используя простейшие приспособления. Пусть решили начертить параболу на листе ватмана. Для удобства закрепим по линии директрисы DD длинную линейку. Воспользуемся достаточно большим прямоугольным треугольником, у которого длинный катет будет всё время параллелен оси OX, а меньший при этом скользит вдоль линейки DD. Прикрепим нить одним концом к вершине острого угла треугольника, а другим – к точке F. Если точу М снабдить пишущим инструментом и всё время обеспечивать натяжение нити и движение точки M вдоль длинного катета (см. рисунок), то на листе ватмана будет вычерчиваться кривая линия – парабола!

Так как уравнение (18) было получено с нарушением тождественности преобразований: применялось возведение в квадрат, то требуется дополнительного исследования уравнения (18). Пусть имеется точка , удовлетворяющая (18). Это значит, что верно:

→ проверим: ==.

Вычислим: ===. Это значит, точка , удовлетворяющая уравнению (18), принадлежит множеству точек парабола! Доказано: условие и уравнение (18) выделяют на плоскости только точки, принадлежащие параболе!

Используя уравнение параболы (18), отметим основные свойства графика параболы:

1). Так как переменная входит в уравнение во второй степени, то график симметричен относительно оси – ось параболы. Точку называют вершиной параболы.

2). Из уравнения параболы следует также, что в случае, когда , график параболы располагается справа от оси , то есть в той же полуплоскости, что и фокус . При значении слева от оси .

3). Если поменять ролями переменные и , то есть воспользоваться записью: , то получим известную их школьной алгебры параболу: . Отметим преимущества записи уравнения параболы в виде : явно показано положение фокуса параболы .

☺☺

Пример 5–04: Найти координаты центра и радиус окружности: .

Решение:

1). Применим выделение полного квадрата по каждой переменной: .

2). Это значит: координаты центра окружности: (4,–3), радиус =3.

Ответ: координаты центра окружности: (4,–3), радиус =3.

Пример 5–05: Составить уравнение эллипса, большая ось которого совпадает с осью и равна 10, а расстояние между фокусами равно 8.

Решение:

1). Пусть уравнение эллипса имеет вид: . Так как 2=8, 2=10, то =4, =5.

2). Так как есть большая полуось, то = 9. Уравнение эллипса: .

Ответ: .

Пример 5–06: Имеем эллипс: . Определить, какие из точек: (4,–3), (2,2), = лежат внутри эллипса, вне эллипса и на эллипсе.

Решение:

1). Из уравнения эллипса имеем: =5, =3. Вычисляем: =4. Воспользуемся формулами для вычисления расстояний точки до фокусов эллипса: =, =.

3). Для точки : ==, ==3. Так как +=+3 >2a , то точка лежит вне эллипса.

4). Для точки : ==, ==. Так как +=+ >2a, то точка лежит вне эллипса.

5). Для точки : ==, ==. Так как +=10 =2a, то точка принадлежит эллипсу.

Ответ: точка принадлежит эллипсу; точки и лежат вне эллипса.

Пример 5–07: Составить уравнение гиперболы, вершины которой находятся в фокусах эллипса: , а фокусы в вершинах того же эллипса.

Решение:

1). На рисунке обозначены фокусы и вершины эллипса. В соответствии с условием задачи будем считать для гиперболы: фокус =, вершина =.

2). Из уравнения эллипса в соответствии с принятыми обозначениями: =4, =3. Используя для эллипса: Вычисляем для фокуса эллипса: =.

3). Используя условие, для гиперболы имеем: =, =4. Используя для гиперболы выражение: , вычисляем: =3 и записываем: – уравнение гиперболы.

4). Интересно параллельно аналитическому решению задачи выполнить построение чертежа. Так, имея большую ось эллипса, строим окружность радиуса . Применяя коэффициент сжатия этой окружности ==, легко строим эллипс. Проводя через фокус эллипса перпендикуляр к оси , отмечаем на окружности точки , , которые определяют асимптоты гиперболы. Применяя лекало, легко построить гиперболу, уравнение которой было получено в пункте 3) решения.

Ответ: уравнение гиперболы: .

Пример 5–08: Осевое сечение отражателя автомобильной фары имеет форму параболы. Пусть глубина фары 10 см, а её диаметр 20 см. Каково положение фокуса этой параболы?

Решение:

1). Уравнение параболы: . Рассматривая сечение фары в плоскости , отметим точку фары: (10, 10). Тогда имеем: , откуда =5.

2). Для параболы фокус определяется выражением: , у нас: .

Ответ: .

☻