1. Применительно к сигналам можно говорить об их классификации.

1. По способу представления сигналы можно описывать с помощью формульной одномерной модели (например: U(t)=U₀cos(t)) или с помощью многомерной векторной модели (например: система напряжений на клеммах многополюсника U(t)={U₁(t), U₂(t)… U_n(t)}).

2. По возможности точного предсказания в любой момент времени электрические сигналы можно разделить на детерменированные (определенные) и случайные. Детерменированные сигналы можно точно определить в любой момент времени и следовательно их можно задать формулой, алгоритмом или таблицей. Случайные сигналы не могут быть точно описаны в любой момент времени. К ним относятся помехи и шумы. Такие сигналы описываются с помощью математического аппарата теории вероятности.

2.1. В рамках детерминированных сигналов вводят понятие импульсных сигналов или импульсов, – т.е. колебаний, которые существуют в пределах конечного отрезка времени.

Различают видеоимпульсы и радиоимпульсы. Примеры видео и радиоимпульсов показаны на рис.1.1. Если U₀(t) – видеоимпульс, то соответствующий ему радиоимпульс имеет вид: U(t)= U₀(t)cos(t+), где  и  произвольны.

2.2. По способу представления в детерминированном виде различают сигналы аналоговые, дискретные и цифровые. Аналоговый сигнал можно представить в виде непрерывной функции. Дискретный сигнал отличается от аналогового тем, что является частью (счетным множеством) аналогового сигнала. Примеры аналогового и дискретного сигналов показаны на рис. 1.2.

U

t

Задается непрерывной функцией

Счетное множество точек аналогового сигнала

а)

а)- аналоговый б)- дискретный

Рис.1.2 Примеры сигналов

Квантование, т.е. дискретизация аналоговых сигналов реализуется электронными устройствами по времени при переменной амплитуде и по амплитуде при переменной длительности рис.1.3.

Рис.1.3 Квантование аналогового сигнала а)- аналоговый; б)- по времени; в)-по амплитуде

Таким образом, любая телекоммуникационная система обрабатывает цифровые, аналоговые, смешанные (цифровые и аналоговые) или дискретные сигналы. Всякая телекоммуникационная система содержит приемник, передатчик и устройства обработки сигнала рис.1.4.

Рис.1.4. Структурная схема телекоммуникационной системы

1. Аналоговый приемно-передающий блок.

2. Цифровой приемно-передающий блок.

3. Аналого-цифровой приемно-передающий блок.

4. Цифро-аналоговой приемно-передающий блок.

Для цифровых передающих систем вводят понятие объем информации, определяемое выражением: (1.1) или ,

где –объем информации (размерность бит или байт), – вероятность нахождения устройства в j состоянии. Пример1.1.

Пусть задан двоичный код. Вероятность нахождения устройства в состоянии 0 или 1 равны 50%, следовательно, . Какой объем информации будет передан, если требуется передать 12 разрядное слово?

Используя соотношение (1.1) легко получить: .

Для систем не двоичного счисления вводят понятие полного объема информации H:

(1.2) Для двоичных систем счисления H совпадает с I.

Чтобы характеризовать передачу информации по линии, вводят понятие скорости передачи информации R: [бит/сек=бот] (1.3) где H - полный объем информации; T – время, которое требуется для передачи полной посылки. В случае двоичной системы счисления H=I и следовательно .

максимальная скорость передачи информации по каналу можно рассчитать, используя следующее соотношение:

(1.4)

где – полоса пропускания канала [Гц], – отношение сигнала к шуму.

Тогда, если , то вероятность ошибок стремится к нулю.

Пример 1.4.

Предположим, что надо передать 12 разрядное двоичное слово через систему связи с полосой пропускания 1 МГц за 1мс, при условии, что отношение сигнал шум . Возможна ли передача информации без ошибок?

Рассчитаем скорость передачи информации по каналу, используя соотношение (1.4):

[бит/с] Рассчитаем R из соотношения (1.3): [бит/с] Так как , то передача информации возможна без ошибок.

2 Сигнал называется периодическим, если значения сигнала, изменяющегося во времени, повторяются через равные промежутки времени, называемые периодом Т. Простейший тип периодических сигналов – это гармонические сигналы, которые описываются выражением

или где - амплитуда сигнала, - фаза сигнала, -начальная фаза сигнала, - угловая частота сигнала.

В радиотехнике и электротехнике большое значение придается гармоническим сигналам. Это обусловлено следующими причинами:

1. Гармонические сигналы инвариантны (неизменны) относительно преобразований осуществляемых стационарными линейными электрическими цепями (т.е. сигнал на выходе также является гармоническим и отличается только амплитудой и фазой).

2. Техника генерирования гармонических сигналов относительно проста.

Если какой-то сигнал можно представить в виде суммы гармонических колебаний с разными частотами, то в этом случае говорят, что осуществлено его спектральное разложение.

Практически любой электрический сигнал можно представить в спектральном виде. Для этого надо воспользоваться его разложением в ряд Фурье, т.е. представить функцию, описывающую сигнал, в виде сходящегося тригонометрического ряда.

Итак, если на отрезке задан ортонормированный базис, образованный гармоническими функциями с кратными частотами:

; ; ; ; (2.1)

и так далее, то любую периодическую функцию n = 1,2...

можно представить в спектральном виде: , ( 2 .2) где - коэффициенты ряда Фурье;  - базис ортонормированных функций (2 1).

Ряд ( 2.2 ) называется рядом Фурье и для него имеется единственное решение. Используя выражения (2.1)  и (2.2) можно для S(t) записать: , ( 2.3)

где коэффициенты определяются по формулам Эйлера-Фурье:

, , (2.3а)

- основная частота.

Отыскание ряда Фурье для сложного гармонического сигнала, называется гармоническим или спектральным анализом. Составляющие этого ряда - циклические частоты, которые равны и т.д., называются соответственно первой (основной), второй, третьей и т.д. гармониками сложного сигнала.

Каждая гармоника ряда Фурье характеризуется амплитудой A_m и начальной фазой _m, и для коэффициентов разложения (2.3а) можно записать: a_m=A_mcos_m, b_m=A_msin_m.

Откуда , где .

Тогда единственное решение (2.3) представляется в более удобном виде

( 2.4 )

3 Найти спектральное преобразование последовательности прямоугольных импульсов с параметрами (см. рис.2.1а) четными относительно , - период сигнала, - длительность импульса, - амплитуда импульса. Отношение называется скважность импульсов.

Из (2.3а),  имеем: ;

Используя выражение (2.3) для представления спектрального разложения сигнала, получим:

График такого спектрального разложения, для двух крайних случаев, когда и , показан на рис.2.1б.

Рис.2.1 Спектральное преобразование последовательности прямоугольных импульсов:

а - вид и параметры прямоугольных импульсов, б - спектральное преобразование

4 Спектральное разложение периодического сигнала можно получить, используя в качестве базиса ортонормированных функций экспоненты с мнимым показателем, т.е.

; ; ; ; , где k = 0, 1, 2...

Тогда ряд Фурье принимает вид: , (2.5) где , C_n - коэффициенты ряда Фурье. Разложение (2.5) иногда представляют в более удобном виде

, (2.5а) где

Выражения (2.5) и (2.5а) являются разложением ряда Фурье в комплексной форме.

Так как n принимает значения от - до +, то из (2.5а) видно, что спектр сигнала содержит компоненты как с положительными, так и с отрицательными частотами. Обычно их объединяют в пары, т.е. по формуле Эйлера

=

Отрицательной частоте соответствует вектор напряжения (см.рис.2.2) из разложения (2.5), вращающийся по часовой стрелки, а положительной частоте - вектор вращающийся против часовой стрелки.

5 Пусть - одиночный импульсный сигнал. Чтобы найти его спектральное разложение надо мысленно дополнить его такими же сигналами периодически следующими через T. Тогда используя спектральное разложение в комплексной форме можно записать:

с коэффициентами разложения: Чтобы вернуться к одиночному импульсу надо период устремить в бесконечность , тогда частоты и будут сколь угодно близки друг к другу и их можно заменить на текущую частоту ( 2.6) Тогда коэффициенты ряда Фурье образуют комплексно-сопряженные пары и , и каждой паре соответствует гармоническое колебание вида:  =  или осуществляя предельный переход, т.е. когда мало отличается от , получим

Рассмотрим бесконечно малый интервал . В рамках этого интервала будет содержаться N пар спектральных составляющих (так как ₁=2/T) с коэффициентами разложения Сn (2.6 ), представляющими собой комплексную амплитуду соответствующего единичного гармонического колебания, т.е. (2.7) Так как в рамках интервала  таких колебаний будет N, то полную комплексную эквивалентную амплитуду получим, домножив (2.7) на 2 и N, т.к. спектр сигнала содержит комплексно сопряженные пары. ; (2. 8 )

Выражение (2.8) называется спектральной плотностью сигнала . С учетом вышесказанного (2.8) принимает вид ( 2.9)

С точки зрения физического смысла спектральную плотность можно представить как коэффициент пропорциональности между длиной малого интервала частот и отвечающей ему амплитудой гармонического сигнала с частотой лежащей внутри .

Пример 2.2. Найти спектральную плотность прямоугольного импульса изображенного на рис.2.3а.

Используя соотношение (2.8) имеем:

Пусть , тогда

График нормированной спектральной плотности представлен на рис.2.3б.

6 Раздел математики - теория вероятности, исследует случайные процессы. Отличительной чертой случайного процесса является то, что его значения (например: напряжение или ток) нельзя заранее предсказать. Поэтому, когда говорят о конкретной величине какого-нибудь случайного процесса (например: напряжение на зажимах разогретого до температуры резистора), то подразумевают его статистическую характеристику. В теории вероятностей введены понятия:

- функции распределения случайной величины , т.е. вероятность того, что случайная величина из множества примет значение, равное или меньшее чем . Для функции распределения справедливы два предельных равенства:

(3.1)

- производная от функции распределения - есть плотность вероятности: . (3.2)

Плотность вероятности удовлетворяет условию нормировки,

т.е. (3.3)

Для случайных величин из множества введены понятия:

• Математическое ожидание ( m ) - среднее значение, которое может принимать случайная величина 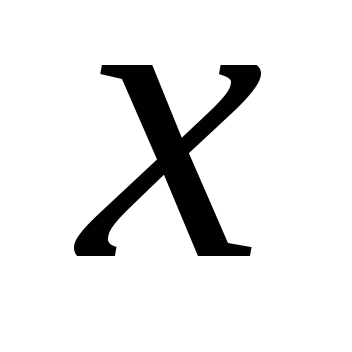: (3.4)

• Дисперсия или среднеквадратичное отклонение , которое характеризует меру разброса результатов испытаний относительно математического ожидания. (3.5)

Пример 1 Равномерное распределение.

Пусть случайная величина может принимать значения из интервала , причем вероятности попадания в любые внутренние интервалы равны.

Функцию распределения находят путем интегрирования плотности вероятности.

График плотности вероятности и функции распределения показан на рис.3.1.Математическое ожидание:

Дисперсия:

Пример 2 : Плотность вероятности Гауссового распределения (рис.3.2), , содержит два параметра . и . График данной функции представляет собой колоколообразную кривую с максимумом в точке .