dsd1-10 / dsd-01=Компоненты ИС / Staroselskiy OLD / 03.bipolary / 4

78

4.Частотные и импульсные свойства коэффициентов передачи тока  и  (нормальный режим)

4.1. Частотные свойства коэффициента передачи эмиттерного тока

Нестационарное биполярное уравнение непрерывности потока неосновных носителей в базе:

. (4.1.1)

Пусть , где — постоянная составляющая эмиттерного тока, — комплексная амплитуда малого гармонический сигнал. Тогда:

.

; (4.1.2) . (4.1.3)

После подстановки (4.1.2,3) уравнение (4.1.1) распадается на 2 уравнения:

одно — стационарное для (решалось ранее), второе — нестационарное для комплексной амплитуды малой гармонической составляющей :

, или , (4.1.4)

где — комплексная диффузионная длина электронов.

Уравнение (4.1.4) в точности совпадает со стационарным уравнением непрерывности с заменой ; граничные условия те же. Поэтому его решение то же, что и решение стационарного уравнения с заменой .

Для стационарного режима коэффициент переноса:

, где .

С учетом , , для малой гармонической составляющей:

.

Вынося множитель , получим:

.

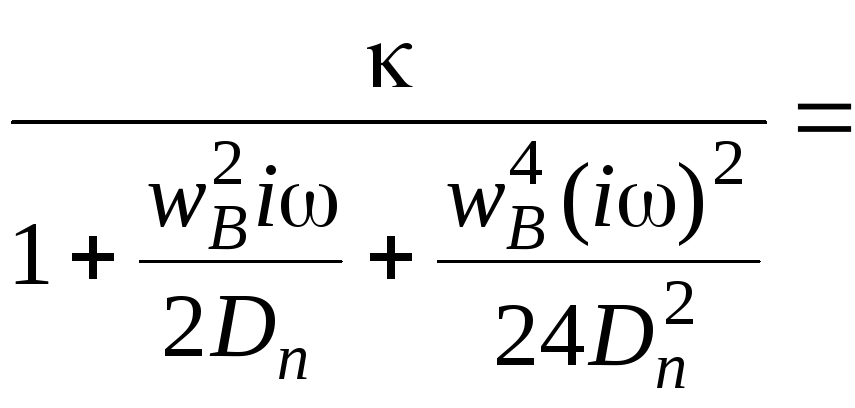
Коэффициент передачи эмиттерного тока

.

До частот эффективность эмиттера практически не зависит от частоты: . При этом:

, (4.1.5)

где — постоянная времени коэффициента передачи

эмиттерного тока, .

На частотах : . (4.1.5а)

Более точная аппроксимация: . (4.1.5б)

. — амплитудно-частотная характеристика (АЧХ);

— фазо-частотная характеристика.

Из (1а): ; .

_ — верхняя граничная частота коэффициента : .

Из (4.1.5а): ; (4.1.6а)

из (4.1.5.б): . (4.1.6б)

4.2. Импульсные свойства коэффициента передачи эмиттерного тока

Частотным характеристикам (4.1.5а,б) соответствуют переходные характеристики

(4.2.1а)

(4.2.1б)

г

1

t/ _

0 0,2 1 2

(t) / 

0

де , — диффузионная задержка.

Е

(1а)

(1б)

сли барьерные емкости , и эмиттерный ток изменяется скачком на в момент , то

.

4.3. Частотные и импульсные свойства

коэффициента усиления базового тока

. Подставляя из (1а), получим:

;

, где . ;

Использование (1б) вместо (1а) практически не изменяет результатов.

При : ; ; .

4.4. Диффузионные емкости в транзисторе

Диффузионные емкости отражают накопление зарядов избыточных носителей в электронейтральных областях базы, коллектора и эмиттера. Их введение приближенно учитывает зависимость коэффициентов передачи тока от частоты.

Диф. емкость эмиттера:

;

  

.

  

Здесь , — время пролета дырок через эмиттер, — время жизни дырок в эмиттере, — дифференциальное сопротивление эмиттерного перехода, — инжектируемая составляющая тока эмиттера (в модели Эберса-Молла — ток диода D₁).

.

Учитывая, что и  0, получим:

. (4.4.1)

По аналогии:

, (4.4.2)

где ,

— инверсное время пролета электронов через базу, — время пролета дырок через коллектор (от базы до подложки, — время жизни дырок в коллекторе, .

На эквивалентной схеме транзистора диффузионные емкости (как и барьерные) включены параллельно диодам, моделирующим р-п переходы.

Введение диффузионных емкостей эквивалентно приближенному учету частотной зависимости коэффициентов . Постоянная времени заряда диффузионной емкости эмиттера через сопротивление — равна постоянной времени коэффициента передачи эмиттерного тока .

Основные результаты

1). Частотная зависимость коэффициента передачи эмиттерного тока определяется соотношением , где .

2). Переходная характеристика коэффициента передачи эмиттерного тока определяется соотношением .

3) При включении транзистора по схеме ОЭ выигрыш в усилении тока равен проигрышу в быстродействии.

4). Накопление избыточных носителей в электронейтральных областях может быть учтено введением диффузионных емкостей эмиттера и коллектора. Произведение диффузионной емкости эмиттерана дифференциальное сопротивление эмиттерного перехода равно потоянной времени .