
dsd1-10 / dsd-06=Kruglov+АИС / LECTIONS / 7_Дискретиз+ТеорияZ
.doc
СПЕКТРЫ ДИСКРЕТИЗИРОВАННЫХ ВО ВРЕМЕНИ СИГНАЛОВ
П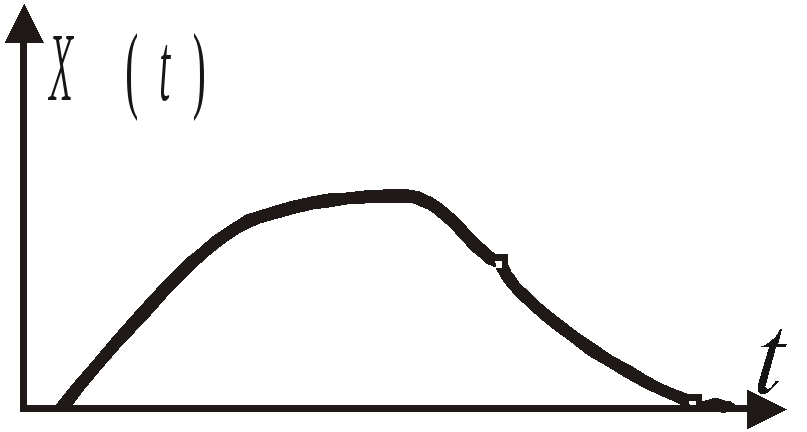 оскольку
концепция Переключаемых Конденсаторов
ПК) содержит дискретизацию во времени,
необходимо учитывать эффекты, являющиеся
следствием дискретизации.
оскольку
концепция Переключаемых Конденсаторов
ПК) содержит дискретизацию во времени,
необходимо учитывать эффекты, являющиеся
следствием дискретизации.
Пусть имеем непрерывный во времени сигнал X(t) (Рис. 3.5.), подаваемый на дискретно – аналоговую систему, на входе которой стоит дискретизатор, представляющий на выходе системы сигнал в дискретном во времени виде с промежутком времени Т (период) между дискретами (Рис.3.6.).
Д
Рис.3.5.
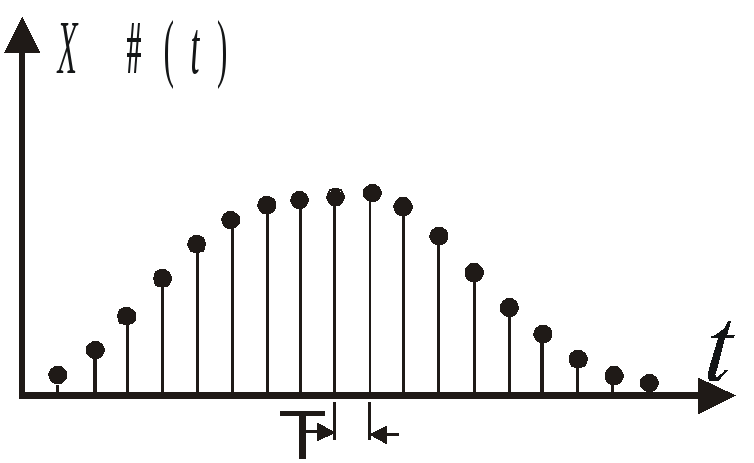
Непрерывный во времени сигнал X(t) Рис.3.6.
Дискретизированный во времени сигнал
X#(t)![]() можно
представить в виде произведения
можно
представить в виде произведения
![]() на
некую функцию
на
некую функцию
![]() ,оставляющую
у
,оставляющую
у
![]() значения только в
значения только в
моменты
![]() ,
где n – целое
,
где n – целое
число:
![]() .
.
Периодичность
функции
![]() однозначно
характеризуется возможностью разложения
ее в ряд Фурье:
однозначно
характеризуется возможностью разложения
ее в ряд Фурье:
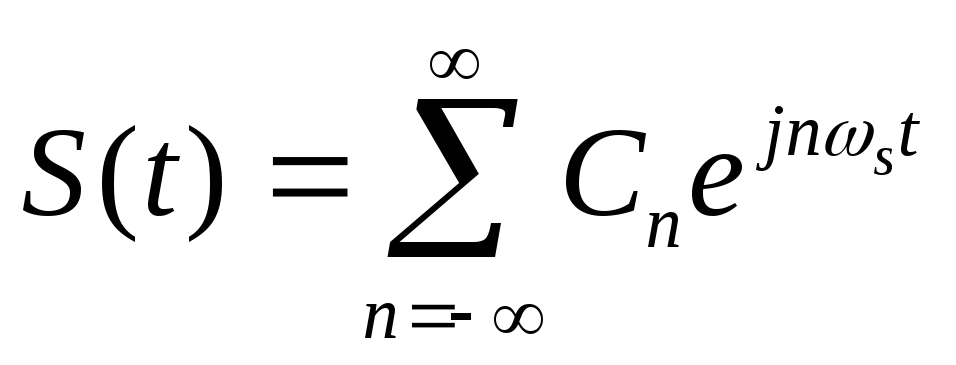
 ,
где
,
где
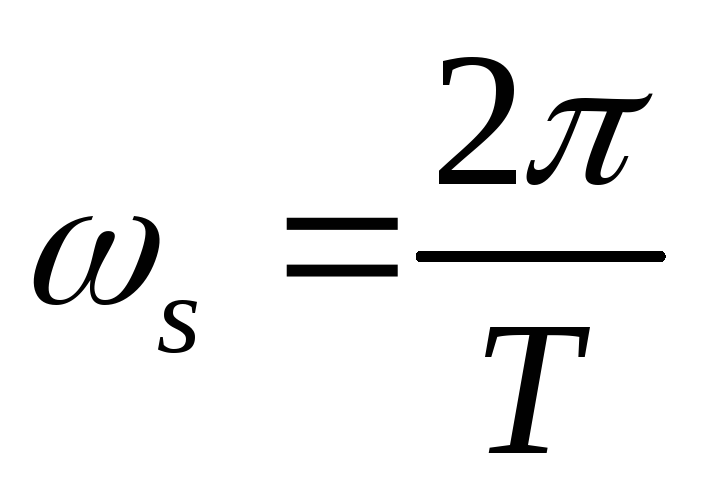 .
.
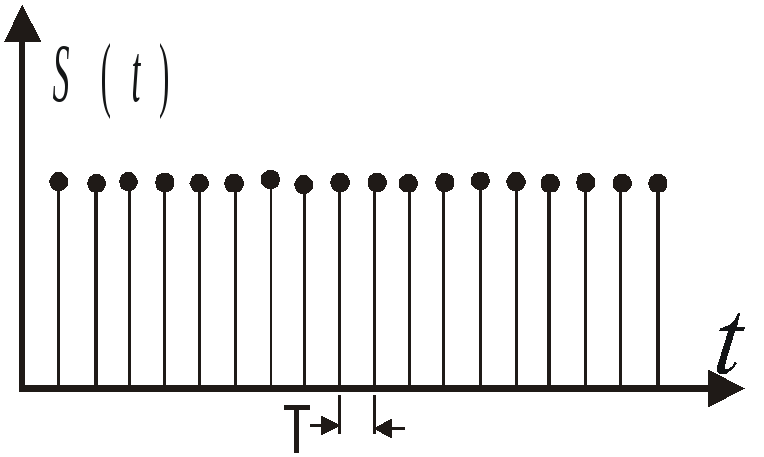
Рис.3.7.
Дискретизирующая функция
Итак:
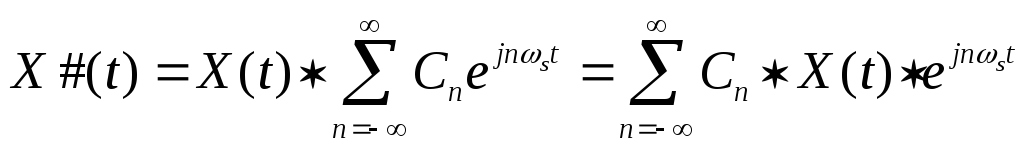
Определим
спектр сигнала
![]() ,
для чего произведем его Фурье –
преобразование:
,
для чего произведем его Фурье –
преобразование:
П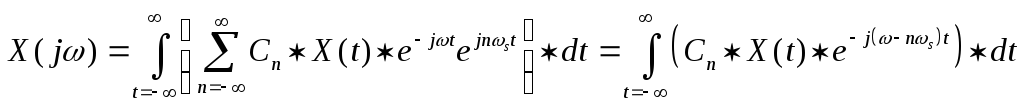 оскольку
оскольку
![]() не зависит от n, умножим
на эту величину каждый член ряда:
не зависит от n, умножим
на эту величину каждый член ряда:
С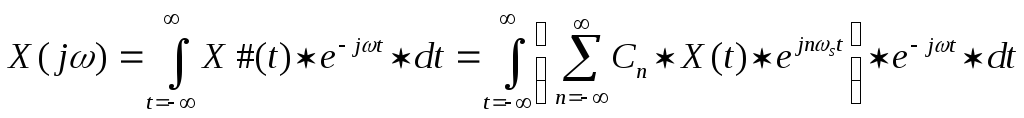 омножитель
омножитель
![]() задает зависимость результата от
частоты. Очевидно, что результат зависит
от значения
задает зависимость результата от
частоты. Очевидно, что результат зависит
от значения
![]() ,
которое принимает одни и те же значения
при частотах
,
которое принимает одни и те же значения
при частотах
![]() ,
периодически изменяющихся с периодом
,
периодически изменяющихся с периодом
![]() . Другими словами, спектральная
характеристика дискретизированного
во времени сигнала
. Другими словами, спектральная
характеристика дискретизированного
во времени сигнала
![]() имеет периодический вид.
имеет периодический вид.
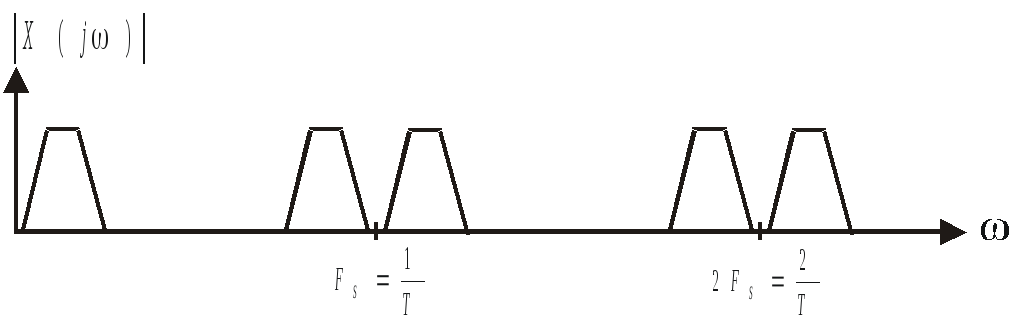
Рис.3.8.
Спектральная характеристика
дискретизированного во времени сигнала
ДИСКРЕТИЗАЦИЯ И Z – ПРЕОБРАЗОВАНИЕ
Излагая введение в Z – преобразование, будем следовать монографии […].
Р Рис.3.9.
Дискретизирующая схема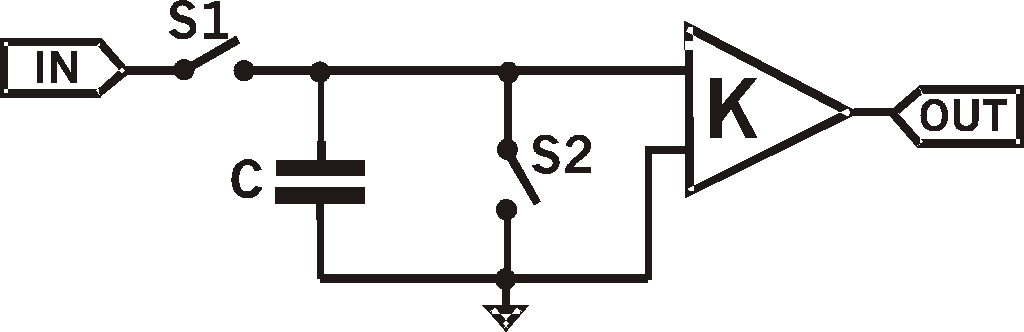
![]() в моменты Т, 2Т, 3Т, … . Это значение
в моменты Т, 2Т, 3Т, … . Это значение
![]() сигнала
держится в течение времени
сигнала
держится в течение времени
![]() ,
и затем ключ S2 мгновенно
разряжает конденсатор до нуля (см.
Рис.3.10). На выходе дискретизатора
находится буфер с коэффициентом усиления
К.
,
и затем ключ S2 мгновенно
разряжает конденсатор до нуля (см.
Рис.3.10). На выходе дискретизатора
находится буфер с коэффициентом усиления
К.
О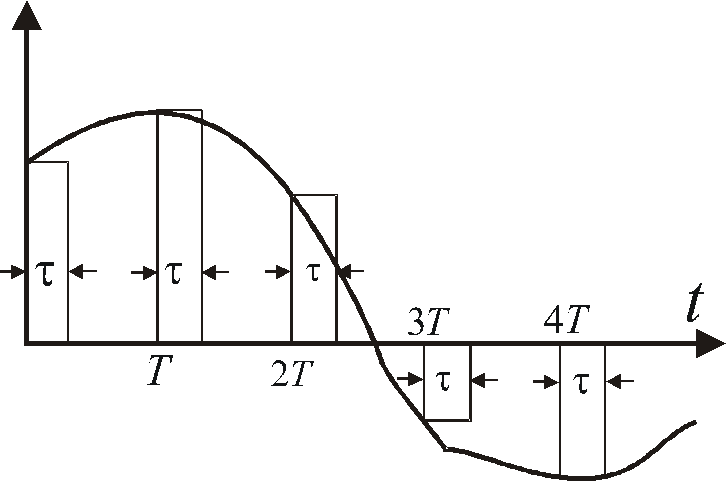 пределим
ступенчатую функцию
пределим
ступенчатую функцию
![]() .
Пусть
.
Пусть
![]() при
при
![]() и
и
![]() при
при
![]() .
Тогда, согласно Рис.3.10, n
– й отсчет функции
.
Тогда, согласно Рис.3.10, n
– й отсчет функции
![]() можно представить в виде:
можно представить в виде:
Рис.3.10.
Дискретизированный эквивалент
непрерывной функции
![]()
![]()
.
Предполагая
![]() при
при
![]() ,
дискретизированный эквивалент
,
дискретизированный эквивалент
![]() этой функции можно записать:
этой функции можно записать:
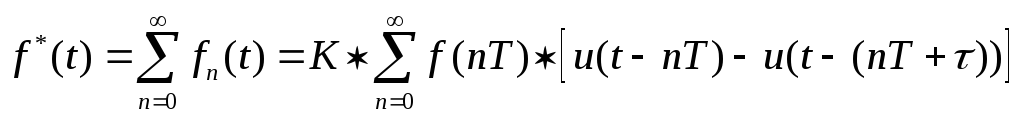 (3.11)
(3.11)
Произведем
для
![]() преобразование
Лапласа и найдем изображение
преобразование
Лапласа и найдем изображение
![]() .
Учитывая что
.
Учитывая что
![]() ,
а также
,
а также
![]() ,
получаем:
,
получаем:
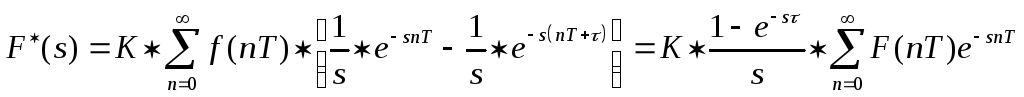
(3.12)
Пусть
ширины
![]() импульсов,
представляющих функцию
импульсов,
представляющих функцию
![]() ,
очень малы, тогда в (3.12) можно записать:
,
очень малы, тогда в (3.12) можно записать:
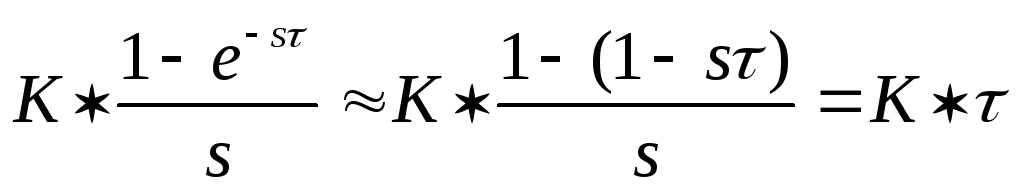 .
(3.13)
.
(3.13)
Для
выражения для
![]() положим
положим
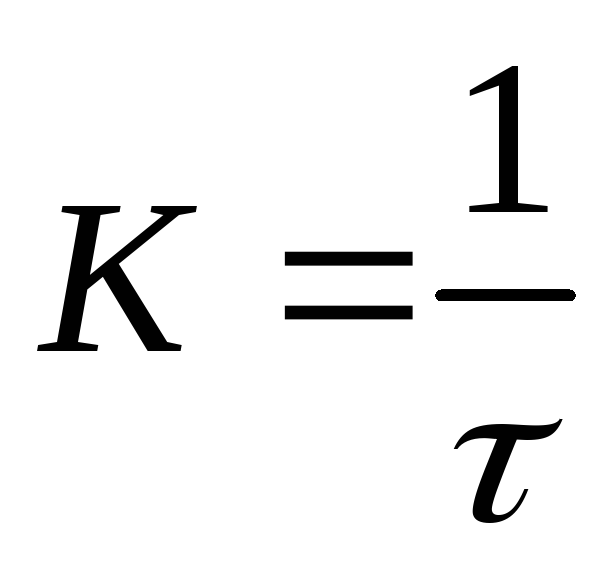 .
Итак, не амплитуда, а площадь каждого
импульса функции
.
Итак, не амплитуда, а площадь каждого
импульса функции
![]() равна
равна
![]() ,
и выражение (3.12) записывается в виде:
,
и выражение (3.12) записывается в виде:
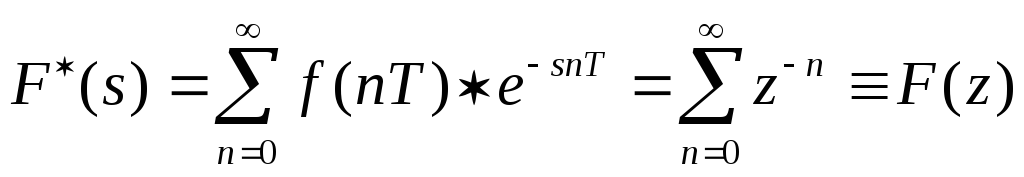 , (3.14)
, (3.14)
где
![]() .
.
Выражение
(3.14) называется Z –
преобразованием дискретных выборок
![]() функции
функции
![]() .
.
Поскольку
Z – преобразование является
таким же интегральным преобразованием,
как и преобразование Лапласа, все
свойства Z – преобразования
повторяют свойства преобразования
Лапласа, но с учетом (3.14), т.е.
![]() .
.
Определим два важных дискретных сигнала – две последовательности.
-
последовательность «единичный импульс»
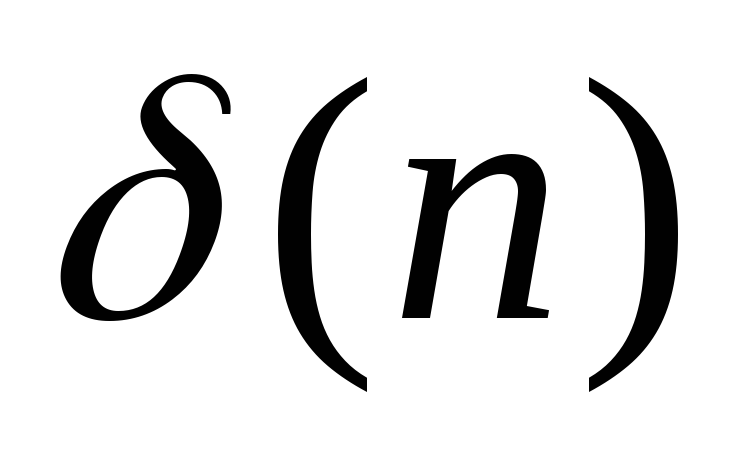 ,
определяемая следующим образом:
,
определяемая следующим образом:
![]() при
при
![]() и
и
![]() при
при
![]() (3.15)
(3.15)
Непрерывный
сигнал
![]() ,
подвергнутый дискретизации и представленный
мгновенными выборками в моменты времени
0, Т, 2T, 3T,
… nT, … можно выразить
через последовательность «единичный
импульс» следующим образом:
,
подвергнутый дискретизации и представленный
мгновенными выборками в моменты времени
0, Т, 2T, 3T,
… nT, … можно выразить
через последовательность «единичный
импульс» следующим образом:
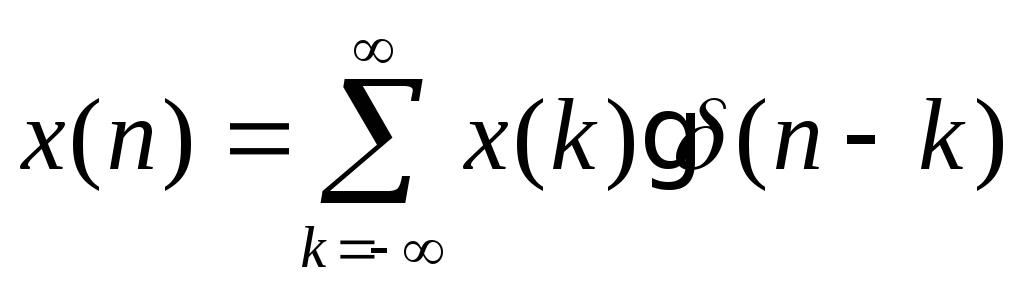 (3.16)
(3.16)
-
последовательность «единичный скачок»
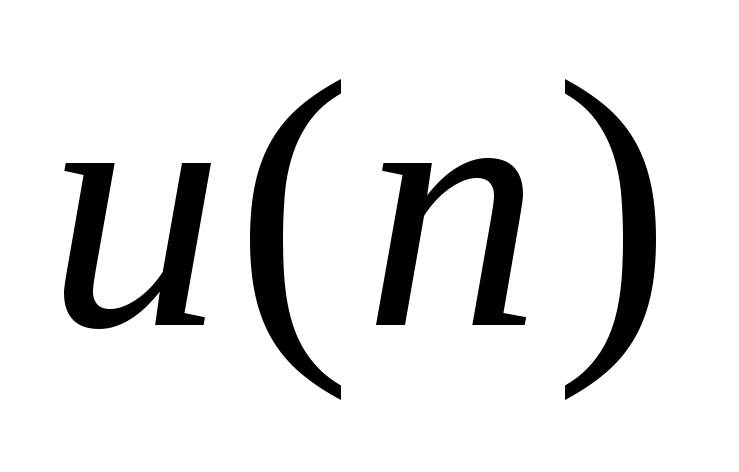 ,
определяемая следующим образом:
,
определяемая следующим образом:
![]() при
при
![]() и
и
![]() при
при
![]() (3.17)
(3.17)
Из определений (3.15) и (3.17) можно показать, что последовательности единичный импульс и единичный скачок связаны соотношениями:
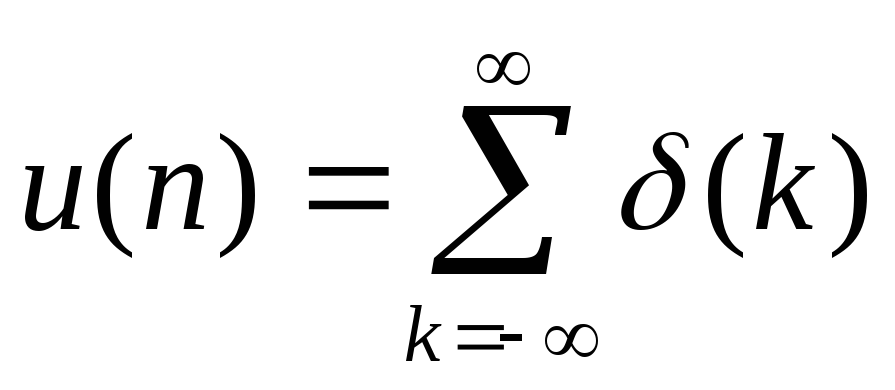 (3.18а)
(3.18а)
![]() (3.18б).
(3.18б).
Пусть
![]() - отклик линейной системы при всех
нулевых начальных условиях на единичный
импульс
- отклик линейной системы при всех
нулевых начальных условиях на единичный
импульс
![]() .
Тогда последовательность
.
Тогда последовательность
![]() является откликом на
является откликом на
![]() .
Из линейности системы и входной
последовательности (3.16) выходная
последовательность задается выражением:
.
Из линейности системы и входной
последовательности (3.16) выходная
последовательность задается выражением:
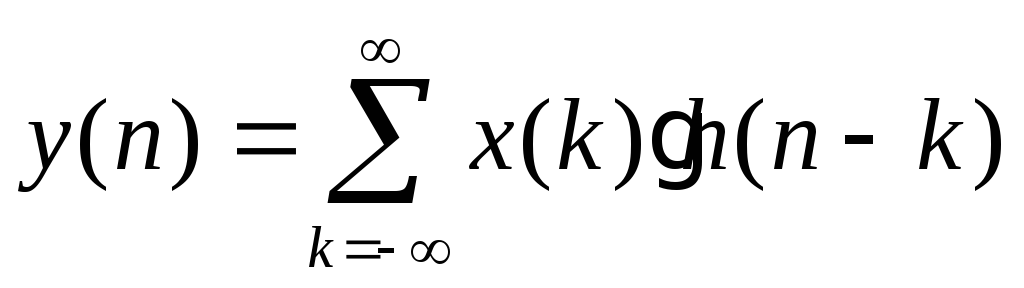 (3.19а)
(3.19а)
Это
означает, что линейная дискретная во
времени система характеризуется
ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКОЙ
![]() ,
т.е. выходной последовательностью при
единичном импульсе на входе и нулевых
начальных условиях. В уравнении (3.19а)
можно заменить переменную, результат
при этом не изменится:
,
т.е. выходной последовательностью при
единичном импульсе на входе и нулевых
начальных условиях. В уравнении (3.19а)
можно заменить переменную, результат
при этом не изменится:
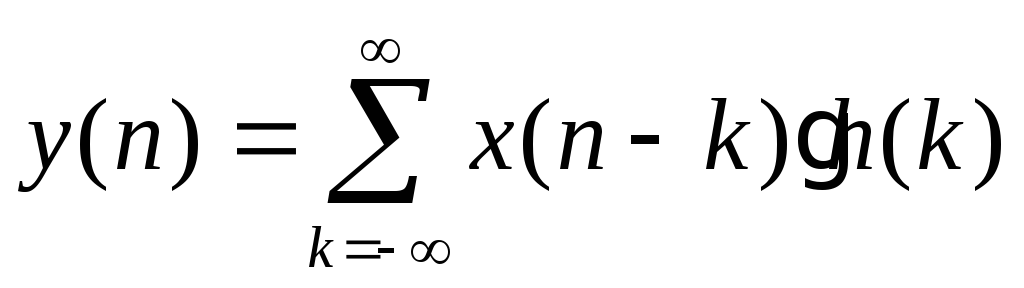 (3.19б)
(3.19б)
Оба
уравнения (3.19а) и (3.19б) обозначают СВЕРТКУ
двух последовательностей
![]() и
и
![]() .
.
Линейная
система называется УСТОЙЧИВОЙ, если
импульсная характеристика
![]() удовлетворяет условию:
удовлетворяет условию:
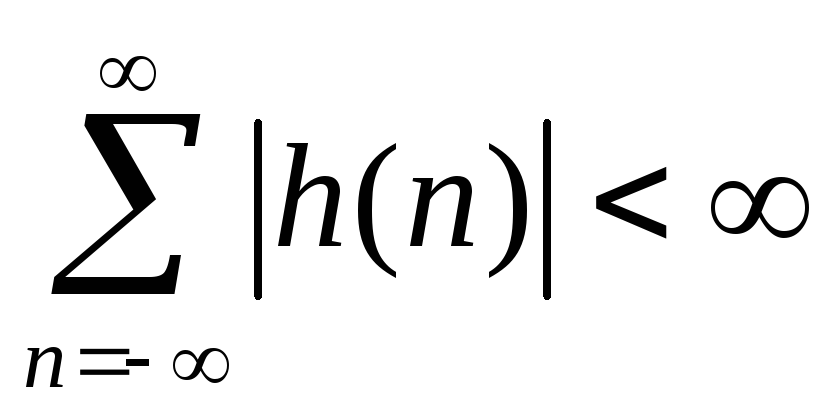 (3.20) и
ФИЗИЧЕСКИ РЕАЛИЗУЕМОЙ, если
(3.20) и
ФИЗИЧЕСКИ РЕАЛИЗУЕМОЙ, если
![]() для
для
![]() .
(3.21)
.
(3.21)
