Отчет к упражнению 1

Составить уравнение плоскости (в отрезках), отсекающей на осях 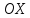и отрезки, соответственно равные 5 и 7, и проходящей через точку .

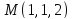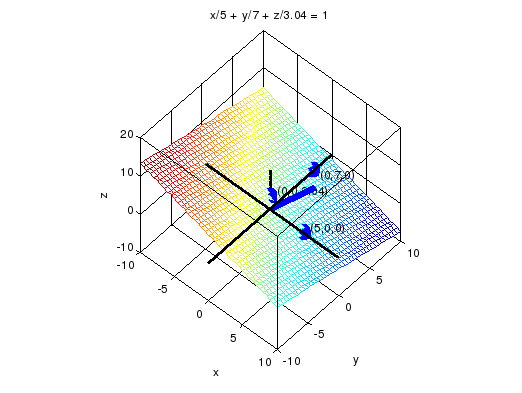
Построить плоскость. Построить нормальный вектор.

В координатном пространстве построить черным цветом толщиной два пункта оси x,y и z, на которых в местах пересечений с плоскостью вывести круговые маркеры синего цвета и обозначить координаты точек пересечения плоскости с осями координат. Вывести обозначение осей и заголовок координатного пространства, в котором написать уравнение плоскости в отрезках.

Так как 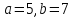, то получаем уравнение плоскости в отрезках:

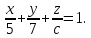
Так как точка М=(1;1;2) принадлежит этой плоскости, то можно подставить ее координ

аты в полученное уравнение:

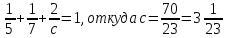
Теперь уравнение плоскости в отрезках имеет вид:

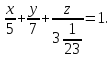
clear all;close all;clc;

a=5;b=7;c=70/23;

x=-10:0.5:10;y=-10:0.5:10;

[X,Y]=meshgrid(x,y);

Z=(1-X/a-Y/b)*c;

hold on;

mesh(X,Y,Z);

plot3(5,0,0,'ob','MarkerSize',8,'LineWidth',4);

text(5,1,0,'(5,0,0)');

plot3(0,7,0,'ob','MarkerSize',8,'LineWidth',4);

text(1,7,0,'(0,7,0)');

plot3(0,0,3.04,'ob','MarkerSize',8,'LineWidth',4);

text(1,0,6,'(0,0,3.04)');

xlabel('x'),ylabel('y'),zlabel('z');

title('x/5 + y/7 + z/3.04 = 1');

box on,axis equal, axis square, grid on

line([0;20/a],[0;20/b],[0;20/c],'LineWidth',4)%строим нормальный вектор

line([-10 0 0;10 0 0],[ 0 -10 0;0 10 0],[ 0 0 -10;0 0 10], 'LineWidth',2, 'Color', 'black' )

view(42,52);

Отчет к упражнению 2

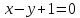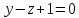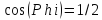Найти с помощью МАТЛАБ угол Phi между плоскостями и . (Угол между плоскостями – это угол между их нормальными векторами. Ответ. ). Построить линию, являющуюся пересечением двух плоскостей, заданных общими уравнениями.(То есть построить обе плоскости). Построить нормальные векторы к плоскостям из точки М принадлежащей обеим плоскостям. Найти направляющий вектор прямой, построить его из начала координат и из точки М. Составить каноническое уравнение прямой и вывести его в названии к графику.

clear all;close all;clc;

n1=[1,-1,0];n2=[0,1,-1];

abs(sum(n1.*n2))/(sqrt(sum(n1.^2))*sqrt(sum(n2.^2)))

ans =

0.5000

clear all;close all;clc;

%построим первую плоскость

x=-20:0.5:20;z=-20:0.5:20;

[X,Z]=meshgrid(x,z);

Y=X+1;

hold on;

plot3(X,Y,Z);

box on;axis equal;axis square;grid on;

%построим вторую плоскость

Y=Z-1;

plot3(X,Y,Z);

%очевидно, что точка М=(-1,0,1) принадлежит обеим плоскостям

plot3(-1,0,1,'om','MarkerSize',8,'lineWidth',4);

text(0,0,1,'M=(-1,0,1)');

%найдем и построим нормальные векторы

n1=20*[1,-1,0];n2=20*[0,1,-1];

line([-1;-1+n1(1)],[0;n1(2)],[1;1+n1(3)],'lineWidth',4);

line([-1;-1+n2(1)],[0;n2(2)],[1;1+n2(3)],'lineWidth',4);

%найдем и построим направляющий вектор

q=cross(n1/20,n2/20)

q =

1 1 1

q=10*q;

line([0;q(1)],[0;q(2)],[0;q(3)],'Color','green','lineWidth',4);

line([-1;-1+q(1)],[0;q(2)],[1;1+q(3)],'Color','red','lineWidth',4);

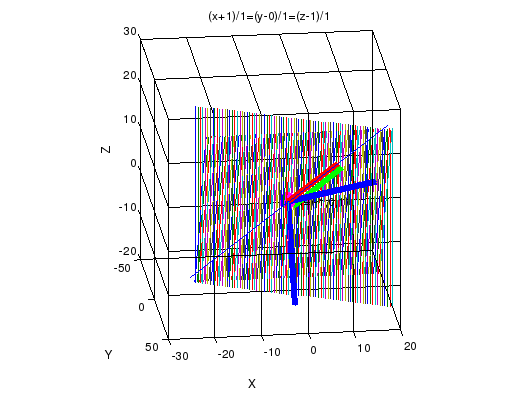
%каноническое уравнение прямой имеет вид (x+1)/1=(y-0)/1=(z-1)/1,

%построим линию пересечения

line([-21;19],[-20;20],[-19;21]);

xlabel('X'),ylabel('Y'),zlabel('Z');

title('(x+1)/1=(y-0)/1=(z-1)/1');