
1 семестр_1 / МА / МП-12_Николаев_Олег_Практ_10 / МП-12_Николаев_Олег_Практ_10
.docxОтчет к упражнению 1
Вычислить
значения первых пяти производных функции
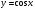 в точке 1, результат записать в текстовый
файл в виде таблицы: первый столбец –
номер производной, второй – значение.
Сделать заголовок и шапку таблицы.
в точке 1, результат записать в текстовый
файл в виде таблицы: первый столбец –
номер производной, второй – значение.
Сделать заголовок и шапку таблицы.
[F, mes]=fopen('t1.txt','w');
fprintf(F,'ТАБЛИЦА ЗНАЧЕНИЙ ПРОИЗВОДНЫХ ФУНКЦИИ cos x \r\n');
fprintf(F,' _________________ \r\n');
fprintf(F,'| i | cos 1 (i) |\r\n');
fprintf(F,' _________________ \r\n');
syms x;
f='cos(x)';
for i=1:1:5
v=subs(diff(f,x,i),x,1);
fprintf(F,'| %d | %7.4f |\r\n',i,v);
end
fclose(F);
ТАБЛИЦА ЗНАЧЕНИЙ ПРОИЗВОДНЫХ ФУНКЦИИ cos x
_________________
| i | cos 1 (i) |
_________________
| 1 | -0.8415 |
| 2 | -0.5403 |
| 3 | 0.8415 |
| 4 | 0.5403 |
| 5 | -0.8415 |
Отчет к упражнению 2
Создать массив ячеек: первая ячейка – значение аргумента, вторая – количество производных, третья - вектор значений функции и её производных в точке из упражнения 2.
m{1}=1;
m{2}=5;
m{3}=[0.5403 -0.8415 -0.5403 0.8415 0.5403 -0.8415];
celldisp(m)
m{1} =
1
m{2} =
5
m{3} =
0.5403 -0.8415 -0.5403 0.8415 0.5403 -0.8415
cellplot(m)

Отчет к упражнению 3
Создать
М-функцию, зависящую от функции, точки,
и числа
 - количества производных, выходным
аргументом которой является вектор
длины
- количества производных, выходным
аргументом которой является вектор
длины
 первый элемент которого – значение
функции в точке, остальные – значения
производных. Проверить работу М-функции
для функций
первый элемент которого – значение
функции в точке, остальные – значения
производных. Проверить работу М-функции
для функций
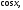

 в точке
в точке
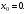
function v=calcdiff(fname,x0,n)
syms x;
for i=0:1:n
v(i+1)=subs(diff(fname,x,i),x,x0);
end
end
calcdiff('cos(x)',0,5)
ans =
1 0 -1 0 1 0
calcdiff('sin(x)',0,5)
ans =
0 1 0 -1 0 1
calcdiff('log(1+x)',0,5)
ans =
0 1 -1 2 -6 24
Отчет к упражнению 4
Создать
М-функцию, входным аргументом которой
является массив, в первой ячейке которого
записана
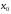 - точка, в окрестности которой происходит
разложение по формуле Тейлора, во второй
число
- точка, в окрестности которой происходит
разложение по формуле Тейлора, во второй
число
 - порядок, до которого происходит
разложение, в третьей – вектор длины
- порядок, до которого происходит
разложение, в третьей – вектор длины
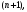 составленный из значений функции и
производных в точке
составленный из значений функции и
производных в точке
 Выходной аргумент – многочлен Тейлора.
Выходной аргумент – многочлен Тейлора.
function f=tay(m)
syms x;
f=sym('0');
for i=0:1:m{2}
f=f+m{3}(i+1).*(x-m{1})^i/factorial(i);
end
end
Для
следующих функций в указанной точке
 построить многочлены Тейлора порядка
построить многочлены Тейлора порядка
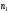 ,
,
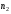 ,
,
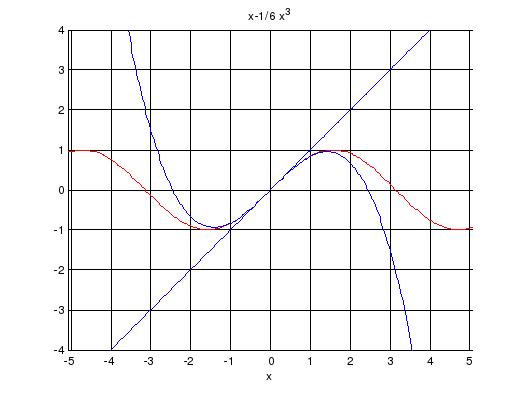
 в одном графическом окне построить
графики функции и многочленов Тейлора:
в одном графическом окне построить
графики функции и многочленов Тейлора:
а)

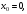

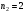 ,
,
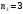 ;
;
grid on;hold on;
syms x;
x0=0;
n1=1;n2=2;n3=3;
f=sin(x);
set(ezplot(f),'Color','r');
f1=tay({x0,n1,calcdiff(f,x0,n1)})
ezplot(f1);
f2=tay({x0,n2,calcdiff(f,x0,n2)})
ezplot(f2);
f3=tay({x0,n3,calcdiff(f,x0,n3)})
ezplot(f3);
axis([-4 4 -4 4]);axis equal;
f1 =
x
f2 =
x
f3 =
x-1/6*x^3
б)
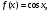
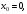
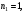
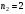 ,
,
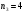 ;
;
grid on;hold on;
syms x;
x0=0;
n1=1;n2=2;n3=4;
f=cos(x);
set(ezplot(f),'Color','r');
f1=tay({x0,n1,calcdiff(f,x0,n1)})
ezplot(f1);
f2=tay({x0,n2,calcdiff(f,x0,n2)})
ezplot(f2);
f3=tay({x0,n3,calcdiff(f,x0,n3)})
ezplot(f3);
axis([-4 4 -4 4]);axis equal;
f1 =
1
f2 =
1-1/2*x^2
f3 =
1-1/2*x^2+1/24*x^4

в)
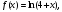

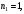
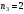 ,
,
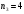 .
.
grid on;hold on;
syms x;
x0=1;
n1=1;n2=2;n3=4;
f=log(4+x);
set(ezplot(f),'Color','r');
f1=tay({x0,n1,calcdiff(f,x0,n1)})
ezplot(f1);
f2=tay({x0,n2,calcdiff(f,x0,n2)})
ezplot(f2);
f3=tay({x0,n3,calcdiff(f,x0,n3)})
ezplot(f3);
axis([-4 4 -4 4]);axis equal;
f1 =
31737720286200319/22517998136852480+1/5*x
f2 =
31737720286200319/22517998136852480+1/5*x-1/50*(x-1)^2
f3 =
31737720286200319/22517998136852480+1/5*x-1/50*(x-1)^2+1/375*(x-1)^3-1/2500*(x-1)^4
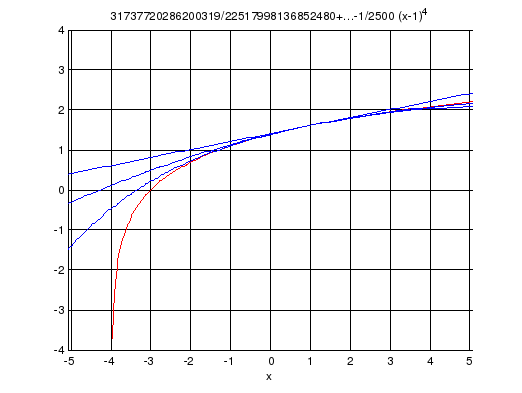
Отчет к упражнению C1
Для
указанной функции в точке
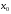 построить многочлены Тейлора порядка
построить многочлены Тейлора порядка
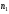 и
и
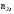 в одном графическом окне построить
графики функции и многочленов Тейлора:
в одном графическом окне построить
графики функции и многочленов Тейлора:
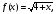

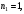
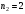 ,
,
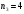 .
.
grid on;hold on;
syms x;
x0=0;
n1=1;n2=2;n3=4;
f=sqrt(4+x);
set(ezplot(f),'Color','r');
f1=tay({x0,n1,calcdiff(f,x0,n1)})
ezplot(f1);
f2=tay({x0,n2,calcdiff(f,x0,n2)})
ezplot(f2);
f3=tay({x0,n3,calcdiff(f,x0,n3)})
ezplot(f3);
axis([-4 4 -4 4]);axis equal;
f1 =
2+1/4*x
f2 =
2+1/4*x-1/64*x^2
f3 =
2+1/4*x-1/64*x^2+1/512*x^3-5/16384*x^4

Отчет к упражнению C2
Воспользуйтесь help, чтобы познакомиться с встроенной функцией taylor. Используя эту функцию, найдите:
а)
многочлены Тейлора 7-го порядка в точке
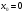 для функций
для функций
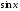 ,
,
 ,
,
 ,
,
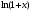 ,
,
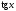 ;
;
syms x;
taylor(sin(x),0,8)
ans =
x-1/6*x^3+1/120*x^5-1/5040*x^7
taylor(cos(x),0,8)
ans =
1-1/2*x^2+1/24*x^4-1/720*x^6
taylor(exp(x),0,8)
ans =
1+x+1/2*x^2+1/6*x^3+1/24*x^4+1/120*x^5+1/720*x^6+1/5040*x^7
taylor(log(1+x),0,8)
ans =
x-1/2*x^2+1/3*x^3-1/4*x^4+1/5*x^5-1/6*x^6+1/7*x^7
taylor(tan(x),0,8)
ans =
x+1/3*x^3+2/15*x^5+17/315*x^7
б)
многочлены Тейлора 5-го порядка в точке
 для функций
для функций
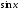 ,
,
 .
.
syms x;
taylor(sin(x),pi/2,6)
ans =
1-1/2*(x-1/2*pi)^2+1/24*(x-1/2*pi)^4
taylor(cos(x),pi/2,6)
ans =
-x+1/2*pi+1/6*(x-1/2*pi)^3-1/120*(x-1/2*pi)^5
