3). Рассмотренная ситуация подсказывает будущему инженеру: в ответственных случаях желательно получить решение несколькими возможными способами!

Пример 3–100: Решить дифференциальное уравнение: –=0, предварительно убедившись, что оно является уравнением в полных дифференциалах.

Решение:

1). Проверим выполнение условия: =. У нас: = и = → заданное уравнение есть уравнение в полных дифференциалах.

2). Вычислим интеграл: ===+.

3). Вычислим производную: =– и запишем условие: =–. Для заданного уравнения: =++=.

4). Вычислим интеграл: ===.

5). Запишем решение: =+=. У нас: +=.

Ответ: += – общее решение.

Пример 4–102: Решить дифференциальное уравнение: , предварительно убедившись, что оно является уравнением в полных дифференциалах.

Решение:

1). Проверим выполнение условия: =. У нас: = и = → заданное уравнение есть уравнение в полных дифференциалах.

2). Вычислим интеграл: ===.

3). Вычислим производную: = и запишем условие: =–. Для заданного уравнения: =.

4). Вычислим интеграл: ==0.

5). Запишем решение: =+=. У нас: =.

Ответ: = – общее решение.

Пример 5–104: Решить дифференциальное уравнение: , предварительно убедившись, что оно является уравнением в полных дифференциалах.

Решение:

1). Проверим выполнение условия: =. У нас: = и = → заданное уравнение есть уравнение в полных дифференциалах.

2). Вычислим интеграл: ===.

3). Вычислим производную: = и запишем условие: =–. Для заданного уравнения: ==.

4). Вычислим интеграл: ===.

5). Запишем решение: =+=. У нас: +=.

Ответ: += – общее решение.

Пример 6–149: Решить дифференциальное уравнение: , предварительно убедившись, что оно является уравнением в полных дифференциалах.

Решение:

1). Проверим выполнение условия: =. У нас: = и = → заданное уравнение есть уравнение в полных дифференциалах.

2). Вычислим интеграл: ===.

3). Вычислим производную: = и запишем условие: =–. Для заданного уравнения: ==.

4). Вычислим интеграл: ===.

5). Запишем решение: =+=. У нас: +=. Воспользовались свойством произвольной постоянной величины .

Ответ: += – общее решение.

Пример 7–154: Решить дифференциальное уравнение: , предварительно убедившись, что оно является уравнением в полных дифференциалах.

Решение:

1). Проверим выполнение условия: =. У нас: = и = → заданное уравнение есть уравнение в полных дифференциалах.

2). Вычислим интеграл: ===.

3). Вычислим производную: = и запишем условие: =–. Для заданного уравнения: ==.

4). Вычислим интеграл: ===.

5). Запишем решение: =+=. У нас: =. Воспользовались свойством произвольной постоянной величины .

Ответ: = – общее решение.

Пример 8–171: Найти уравнение кривой, проходящей через точку , если для любого отрезка [1,x] площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, на 2 больше отношения абсциссы концевой точки к ординате .

Решение:

1) Так как вычисление площади требует применения интеграла, то в соответствии с условием задачи запишем равенство: =+2. Как решают такие уравнения, мы не знаем: изучаем дифференциальные уравнения и, вдруг, в равенстве появился интеграл!.. Для перехода к известным образам продифференцируем равенство с интегралом по переменной . Получаем: . (1)

2) Так как по условию , уравнение (1) можно записать в виде: . (2)

3). Уравнение (2) есть уравнение Бернулли в стандартной форме для значения, при этом имеем: = и =.

2). Применим подстановку: = и перепишем (1) как: , то есть: , или , где =, =.

3). Далее применяем стандартный алгоритм решения линейного уравнения: , записанного в стандартной форме, приняв .

4). Вычисляем интеграл: == и записываем выражение: ==.

5). Вычисляем: =+=+ =+.

6). Запишем общее решение уравнения: =∙, или =. По условию: кривая проходит через точку , получим частное решение: =.

Ответ: =– общее решение; частное решение: =.

Пример 8–187: Скорость охлаждения тела пропорциональна разности температур тела и окружающей среды (закон Ньютона). Найти зависимость температуры от времени , если тело, нагретое до градусов, внесено в помещение, температура которого постоянна и равна градусам.

Решение:

Замечание: рисунок «мотивирует» решение за­да­чи, а также «намекает», что охлаждение тела происходит за счет «молекулярного взаимодействия» тела и среды: подвеска тела к потолку на тонкой нити с минимальной теплопроводностью.

1). Из условия задачи следует дифференциальное урав­не­ние: . (1)

2). Уравнение (1) – ДУ с разделяющимися переменными. Его интегрирование не представляет труда: . (2)

3). Учитывая начальные условия, из уравнения (2) получаем: – закон охлаждение тела в заданных условиях.

Ответ: – общее решение уравнения. Частное решение: .

☻

Вопросы для самопроверки:

1. Как определяют ДУ в полных дифференциалах?

2. Как определить, что данное уравнение есть ДУ в полных дифференциалах?

3. Каков «стандартный алгоритм» решения ДУ в полных дифференциалах?

4. Что такое «интегрирующий множитель уравнения»?

5. Привести пример применения ДУ для решения задачи из геометрии.

6. Привести пример применения ДУ для решения задачи из физики.

Задачи для самоподготовки:

Пример C5–1: Решить дифференциальное уравнение: , пред­варительно убедившись, что оно является уравнением в полных дифференциалах.

Ответ: += – общее решение ДУ.

Пример C5–2: Решить дифференциальное уравнение: +=0, пред­варительно убедившись, что оно является уравнением в полных дифференциалах.

Ответ: += – общее решение ДУ.

Пример C5–3: Решить ДУ: +=0, пред­варительно убедившись, что оно является уравнением в полных дифференциалах

Ответ: = – общее решение ДУ.

Пример C5–4: Решить дифференциальное уравнение: +=0, пред­варительно убедившись, что оно является уравнением в полных дифференциалах.

Ответ: = – общее решение ДУ.

Пример C5–5: Решить ДУ: +=0, пред­варительно убедившись, что оно является уравнением в полных дифференциалах.

Ответ: = – общее решение ДУ.

Пример C5–6: Решить дифференциальное уравнение: –=0, пред­варительно убедившись, что оно является уравнением в полных дифференциалах

Ответ: – частное решение.

Пример C5–7: Найти уравнение кривой, проходящей через точку (1,2), если произведение абсциссы точки касания на абсциссу точки пересечения нормали с осью равно удвоенному квадрату расстояния от начала координат до точки касания.

Ответ: Случай-1: ; Случай-2: – частные решения ДУ.

Пример C5–8: Через сколько времени температура тела, нагретого до 100⁰C, понизится до 25⁰C, если температура помещения равна 20⁰C и за первые 10 мин тело охладилось до 60⁰C?

Ответ: t ≈ 40 мин.

•• ☻☻ ••

ЗАНЯТИЕ 6. Уравнения первого порядка, не разрешенные относительно производной.

Ауд.

Л-2, Гл. 10

№ 114, 116, 118, 120, 122,124.

6

☺ ☻ ☺

Если Дифференциальное уравнение 1-порядка записано в виде: , то говорят, что это уравнение – неразрешённое относительно !..

Рассмотренные ранее типы уравнений: уравнения с разделяющимися переменными, линейные, однородные... достаточно просто можно было разрешить относительно . Теперь мы рассмотрим такие уравнения, которые:

• достаточно сложно приводятся к форме записи уравнения ;

• принципиально не могут быть приведены к форме записи уравнения .

Мы рассмотрим только некоторые из типов уравнений, неразрешённых относительно производной , а именно:

1. Левая часть уравнения есть многочлен n-ой степени относительно символа : , (1)

где – функции от переменных: (в частном случае постоянные).

В высшей алгебре доказано, что многочлен левой части уравнения (1) в любом случае может быть преобразован в произведение простейших множителей:

. (2)

Из записи (2) следует уравнений 1-го порядка: , . Решение каждого такого уравнения даст функцию , являющуюся решением уравнения (1).

Замечание: На самом деле, начиная с многочлена 3-й степени, процесс разложения многочлена в произведение простейших скобок весьма трудоёмкий!..

2. Уравнение, разрешенное относительно y и не содержащее x: . Для решения таких уравнений разработан специальный способ – поиск решения в параметрической форме:

• Примем: =, то есть . Перепишем исходное уравнение: . Так как есть некоторая функция переменной , то и .

• Имея: , запишем . В то же время . Учитывая оба выражения для дифференциала , нетрудно записать: = – уравнение с разделяющимися переменными.

• Учтём решение , то есть . Принимая , можем записать: =, интегрированием которого получаем: =.

• Составим систему: – это параметрическое решение уравнения .

3. Уравнение, разрешенное относительно x и не содержащее y: . Для решения таких уравнений разработан специальный способ – поиск решения в параметрической форме:

• Примем: =, то есть . Перепишем исходное уравнение: .

• Имея: , запишем . В то же время . Учитывая оба выражения для дифференциала , нетрудно записать: = – уравнение с разделяющимися переменными.

• Интегрируя уравнение: = получаем: =.

• Составим систему: – это параметрическое решение уравнения .

4. Уравнение, разрешенное относительно y и содержащее x: . Для решения таких уравнений применяют специальный способ – поиск решения в параметрической форме:

• Примем: =, то есть . Перепишем исходное уравнение: . Так как есть некоторая функция переменной , то и .

• Воспользуемся формулой дифференцирования сложной функции по переменной , именно: =. Заменяя =, получим: =.

• Составим систему: – из этой системы находят решение в явном или параметрическом виде.

Замечание: Рассмотренные в этом Занятии примеры вполне иллюстрируют особенности решения подобных задач!..

5. Уравнение Лагранжа: . Для решения таких уравнений разработан специальный способ – поиск решения в параметрической форме:

• Примем: =, то есть . Перепишем исходное уравнение: .

• Дифференцируем по переменной : . Учитывая =, запишем: .

• Выделим решение . Может быть получено несколько решений:, каждое из которых дополнительно анализируют после получения общего решения!

• Теперь . Учитывая =, перепишем: в виде линейного уравнения: –=. Пусть его решение: .

• Составим систему: – общий интеграл уравнения Лагранжа.

••• ≡ •••

Пример 1–114: Найти общее решение уравнения: в параметрической форме.

Решение:

Замечание: Заданное уравнение представляется многочленом 3-го порядка и разложение его в произведение скобок выполняется трудоёмко!..

1). Форма записи уравнения имеет вид: . Это специальная форма уравнения, неразрешённого относительно . Для решения таких уравнений разработан специальный способ – поиск решения в параметрической форме.

2). Примем: =, то есть . Перепишем исходное уравнение: . Так как есть некоторая функция переменной , то и .

3). Имея: , запишем , где =. В то же время . Учитывая оба выражения для дифференциала , нетрудно записать: =. В нашем случае: = – уравнение с разделяющимися переменными!

4). Учтём решение , то есть . Принимая , можем записать: =, которое легко интегрируется: =, то есть =.

5). Составим систему: , или – это параметрическое решение.

Замечание: Можно было бы попробовать выразить из системы решение в виде: . В нашем случае лучше не пробовать!..

Ответ: – общее решение в параметрической форме. Решение – особое.

Замечание: Решение называют особым, если оно не может быть получено из общего решения ни при каком значении произвольной постоянной!..

Пример 2–116: Найти общее решение уравнения: в параметрической форме.

Решение:

1). Форма записи уравнения имеет вид: . Примем: =, то есть . Перепишем исходное уравнение: =. Так как есть некоторая функция переменной , то и .

2). Имея: , запишем , где =. В то же время . Учитывая оба выражения для дифференциала , нетрудно записать: =. В нашем случае: = – уравнение с разделяющимися переменными!

3). Учтём решение , то есть . Принимая , можем записать: =, которое легко интегрируется: =, то есть =.

4). Составим систему: , или – это параметрическое решение.

Замечание: Можно было бы попробовать выразить из системы решение в виде: . В нашем случае лучше не пробовать: не получится!..

Ответ: – общее решение в параметрической форме.

Пример 3–118: Найти общее решение уравнения: в параметрической форме.

Решение:

1). Форма записи уравнения имеет вид: . Примем: =, то есть . Перепишем исходное уравнение: =.

2). Имея: , запишем , где =. В то же время , или: =. В нашем случае: = – уравнение с разделёнными переменными!

3). Интегрируем уравнение: ==, или =.

4). Составим систему: , или – это параметрическое решение.

Замечание: Можно было бы попробовать выразить из системы решение в виде: . В нашем случае лучше не пробовать!..

Ответ: – общее решение в параметрической форме.

Пример 4–120: Найти общее решение уравнения: в параметрической форме.

Решение:

1). Форма записи уравнения имеет вид: . Примем: =, то есть . Перепишем исходное уравнение: =.

2). Имея: , запишем , где =. В то же время , или: =. В нашем случае: = – уравнение с разделёнными переменными!

3). Интегрируем уравнение: ==, или =.

4). Составим систему: , или – это параметрическое решение.

Замечание: Можно было бы попробовать выразить из системы решение в виде: . В нашем случае лучше не пробовать!..

Ответ: – общее решение в параметрической форме.

Пример 5–122: Найти решение уравнения Лагранжа: , применяя метод введения параметра.

Решение:

1). Форма записи уравнения имеет вид: – уравнения Лагранжа в общем виде. В нашем случае: = и =0.

2). Примем: =, то есть . Перепишем исходное уравнение: . В нашем случае: =.

3). Дифференцируем по переменной : . Учитывая =, запишем: . В нашем случае: =, производная = и =0. Тогда уравнение имеет вид: =

4). Выделим решение . В нашем случае: =0. Получено:, , или, используя: , можем записать решения исходного уравнения: . Эти решения проанализируем после получения общего решения!..

5). Теперь . Учитывая =, перепишем: в виде:

–= – линейное уравнение,

решая последнее, получим . В нашем случае: , его решение: .

6). Cоставим систему: у нас: – общий интеграл заданного

Ответ: – общий интеграл заданного уравнения. Особое решение: y = ±x.

Пример 6–124: Найти решение уравнения Лагранжа: , применяя метод введения параметра.

Решение:

1). Форма записи уравнения имеет вид: – уравнения Лагранжа в общем виде. В нашем случае: = и =.

2). Примем: =, то есть . Перепишем исходное уравнение: . В нашем случае: .

3). Дифференцируем по переменной : . Учитывая =, запишем: . В нашем случае: =, производная = и =. Тогда уравнение имеет вид: =.

4). Выделим решение . В нашем случае: =0. Получено:, , или, используя: , можем записать решения исходного уравнения: и . Эти решения проанализируем после получения общего решения!..

5). Теперь . Учитывая =, перепишем: в виде:

–= – линейное уравнение,

решая последнее, получим . В нашем случае: , его решение найдём применением общего алгоритма решения линейного уравнения:

• Решение уравнения ищем в виде функции: .

• Вычислим: ==, и запишем: u=, то есть .

• Вычислим: ==+, и запишем.

• Запишем общее решение линейного уравнения: =∙. Если последнее записать в виде: =∙+ и в первой дроби выполнить преобразование выделение целой части, то =.

6). Вычислим: =, и запишем:

Ответ: – решение уравнения в параметрической форме. Особые решения: и .

☻

Вопросы для самопроверки:

1. Как определяют уравнение 1-го порядка, не разрешённое относительно производной?

2. Основные типы уравнений, не разрешённых относительно производной.

3. Как вводят параметр при решении уравнения y=φ(y′)?

4. Как вводят параметр при решении уравнения x=φ(y′)?

5. Как вводят параметр при решении уравнения F(y,y′)=0?

6. Как вводят параметр при решении уравнения F(x,y′)=0?

7. Что такое «Уравнения Лагранжа»?

8. Привести пример применения ДУ для решения задачи из геометрии.

9. Привести пример применения ДУ для решения задачи из физики.

Задачи для самоподготовки:

Пример C6–1: Найти общее решение уравнения: в параметрической форме.

Ответ: 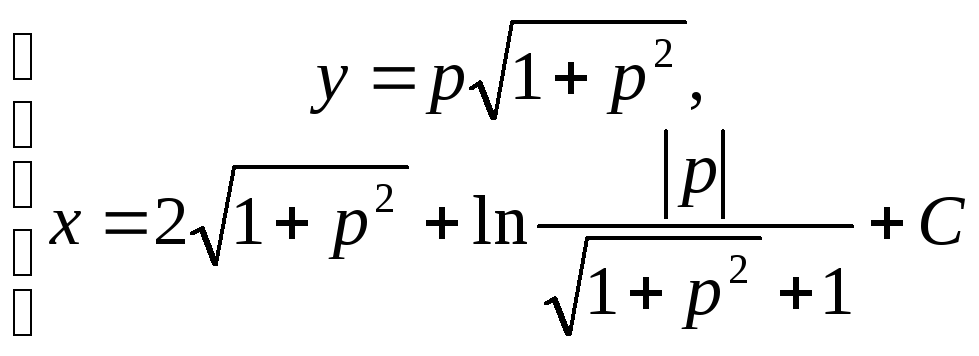– общее решение в параметрической форме. Решение – особое.

Пример C6–2: Найти общее решение уравнения: .

Ответ: – общее решение уравнения. Решение – особое.

Пример C6–3: Найти общее решение уравнения: .

Ответ: – общее решение в параметрической форме.

Пример C6–4: Найти общее решение уравнения: 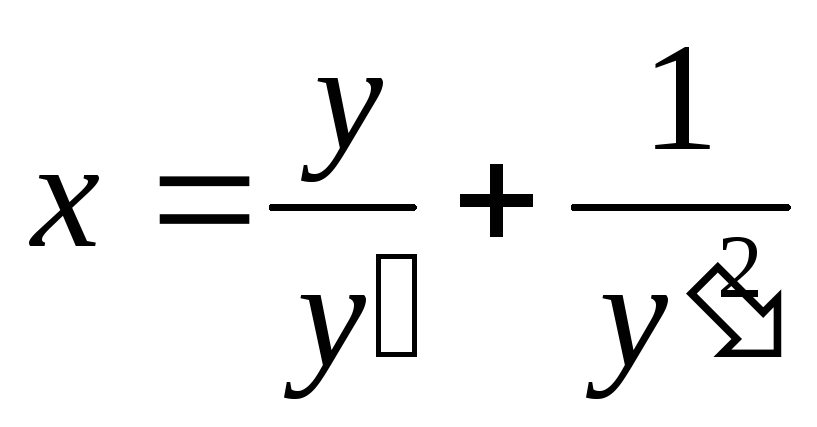в параметрической форме.

Ответ: – общее решение, – особое решение.

Пример C6–5: Найти решение уравнения Лагранжа, применяя метод введения параметра.

Ответ: – решение уравнения в параметрической форме.

Пример C6–6: Найти решение уравнения Лагранжа, применяя метод введения параметра.

Ответ: – решение уравнения в параметрической форме.

Пример C6–7: Найти уравнение кривой, проходящей через точку (3,1), если длина отрезка оси абсцисс, отсекаемого любой ее касательной на оси ординат, равна поднормали.

Ответ: или – частные решения для: =1.

•• ☻☻ ••

ЗАНЯТИЕ 7. Повторение: все типы уравнений 1-го порядка. Обзорные упражнения: определение типа дифференциального уравнения и обсуждение общего алгоритма решения. Систематизация знаний. Подготовка к контрольной работе.

☺ ☻ ☺

Систематизация знаний по ДУ 1-го порядка предполагает повторение основных понятий теории Дифференциальных уравнений с их толкованием и примерами использования при решении заданных ДУ и при решении простых геометрических и физических задач.

Повторение темы Классификация различных дифференциальных уравнений предполагает быстрое распознавание произвольно выбираемых из Задачника примеров.

Применение общих алгоритмов решения ДУ первого порядка при рассмотрении конкретного уравнения проводится с соблюдением принципов обоснованности (правомерности) последовательно применяемых шагов решения.

Основные требования по оформлению решения любого уравнения при выполнении домашнего Задания и Контрольной работы.

Замечание: 1). При подготовке к настоящему Занятию необходимо тщательно повторить материал Глав 1-5 Пособия по Дифференциальным уравнениям для факультета ЭТМО 1-го курса.

2). Предполагается за время проведения Занятия оценить степень готовности к выполнению Контрольной работы по ДУ № 1 всех студентов группы!..

•• ☻☻ ••

ЗАНЯТИЕ 8. Уравнения 1-го порядка. Контрольная работа №1. Прием части-1 БДЗ. Выдача части-2 БДЗ.

☺ ☻ ☺

Контрольная работа №1 предназначена оценить степень усвоения основных понятий теории Дифференциальных уравнений и способов решения простейших типов ДУ первого порядка:

• Уравнения первого порядка с разделяющимися переменными.

• Однородные уравнения первого порядка. Уравнения специального вида, приводящиеся к однородному уравнению 1-го порядка.

• Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли.

• Уравнения в полных дифференциалах.

• Уравнения 1-го порядка, не разрешённые относительно производной.

Состав и степень трудности предлагаемых в Контрольной работе заданий согласовывается с Методическим советом кафедры «Высшая математика».

При разработке заданий Контрольной работы учитывается также требование побудить студентов повторить пройденный материал по предмету. Это значит, что в заданиях не должно быть ничего такого, что, так или иначе, требует самостоятельных обобщений и выводов со стороны студентов.

Перед выполнением Контрольной работы студенты должны ознакомиться с перечнем вопросов, которые будут отражены в заданиях. Также важным элементом подготовки к контрольной работе должны быть регулярные текущие контрольные мероприятия в виде оперативных опросов: по 6-7 минут в начале каждого занятия.

Прием части-1 БДЗ определяется двумя последовательными мероприятиями:

1). Формальный приём выполненных Заданий непосредственно в аудитории: проверка на соответствие правилам закрепления вариантов заданий за каждым студентом.

2). Защита выполненных заданий БДЗ каждым студентом в специально назначенное время (обычно, в день консультаций по предмету). Определение окончательной оценки качества выполнения Части-1 БДЗ.

Замечание: 1). Сборник заданий по БДЗ находится в информационной системе института с самого начала семестра, постоянно.

2). Сборник заданий по БДЗ содержит по каждому заданию примеры решения и оформления.

•• ☻☻ ••