
- •Глава 4. Плоскость и прямая в пространстве § 1. Векторное и смешанное произведение векторов
- •Выражение векторного произведения через координаты векторов
- •Геометрический смысл смешанного произведения
- •Выражение смешанного произведения через координаты векторов
- •Условия коллинеарности и компланарности векторов
- •Задачи для самостоятельного решения
- •§ 2. Уравнения прямых и плоскостей в пространстве
- •§ 3. Расстояние и отклонение точки от плоскости
- •§ 4. Расстояние от точки до прямой в пространстве. Расстояние между скрещивающимися прямыми
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
Вычислить угол между прямой
 и плоскостью
и плоскостью Ответ:
Ответ: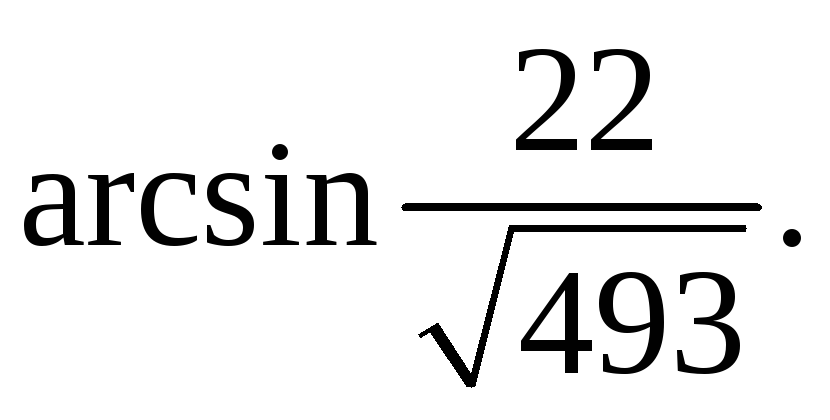
Составить уравнение плоскости, проходящей через точку
 параллельно плоскости
параллельно плоскости Ответ:
Ответ:
Составить уравнение плоскости, проходящей через точки

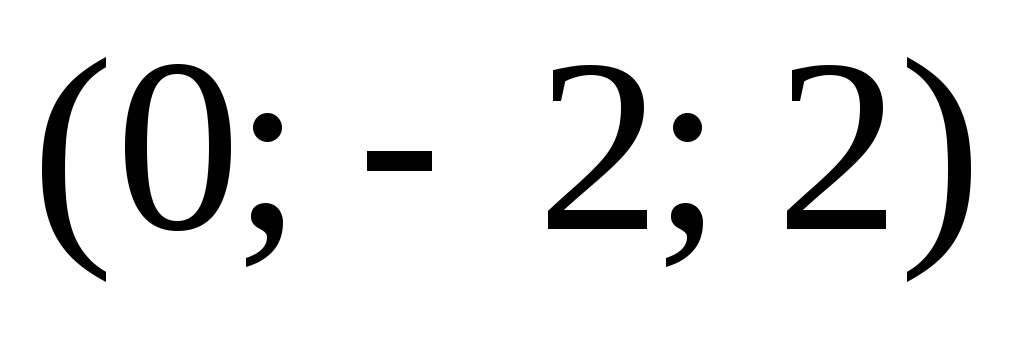 и параллельной прямой
и параллельной прямой Ответ:
Ответ:
Составить уравнение плоскости, проходящей через ось ординат и точку
 Ответ:
Ответ:
Составить уравнение геометрического места точек, равноудалённых от точек
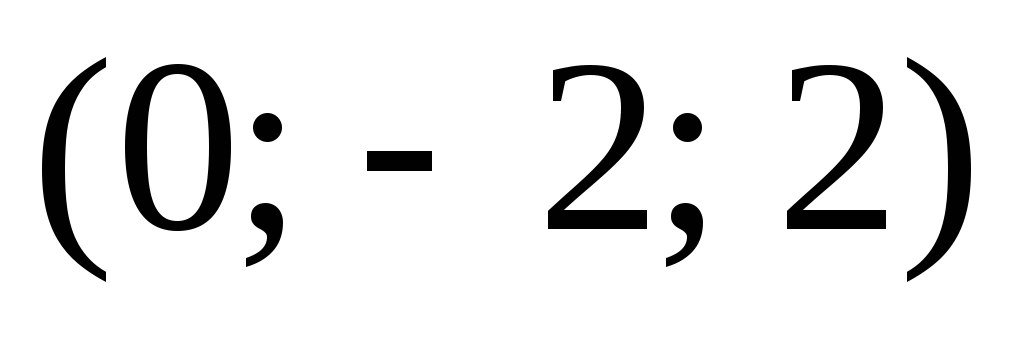 и
и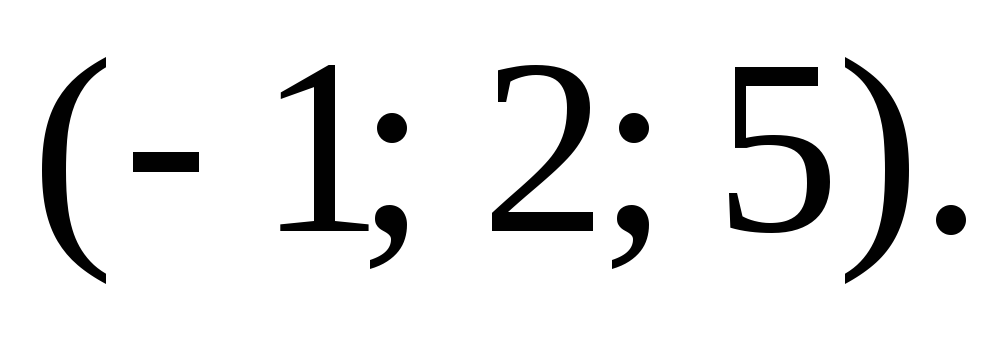 Ответ:
Ответ:
Составить уравнение прямой, проходящей через точку
 параллельно прямой
параллельно прямой Ответ:
Ответ:
Через точку
 провести прямую, перпендикулярную
плоскости
провести прямую, перпендикулярную
плоскости Ответ:
Ответ:
Через прямую
 провести плоскость, параллельную прямой
провести плоскость, параллельную прямой Ответ:
Ответ:
Через точку
 провести плоскость, перпендикулярную
плоскостям
провести плоскость, перпендикулярную
плоскостям и
и Ответ:
Ответ:
Составить уравнение плоскости, симметричной плоскости
 а) относительно начала координат, б)
относительно оси
а) относительно начала координат, б)
относительно оси в) относительно плоскости
в) относительно плоскости г) относительно плоскости
г) относительно плоскости д) относительно точки
д) относительно точки Ответ: а)
Ответ: а) б)
б) в)
в) г)
г) д)
д)
Составить уравнение прямой, симметричной прямой
 а) относительно начала координат, б)
относительно оси
а) относительно начала координат, б)
относительно оси в) относительно плоскости
в) относительно плоскости г) относительно плоскости
г) относительно плоскости д) относительно точки
д) относительно точки Ответ: а)
Ответ: а) б)
б) в)
в) г)
г) д)
д)
Найти точку пересечения плоскости
 и прямой, проходящей через точки
и прямой, проходящей через точки и
и Ответ:
Ответ:
При каких
 прямая
прямая а) параллельна плоскости
а) параллельна плоскости б) перпендикулярна этой плоскости?
Ответ: а)
б) перпендикулярна этой плоскости?
Ответ: а) б) таких
б) таких нет.
нет.При каких
 прямые
прямые и
и – скрещивающиеся? Ответ:
– скрещивающиеся? Ответ:
Спроектировать точку
 на плоскость
на плоскость Ответ:
Ответ: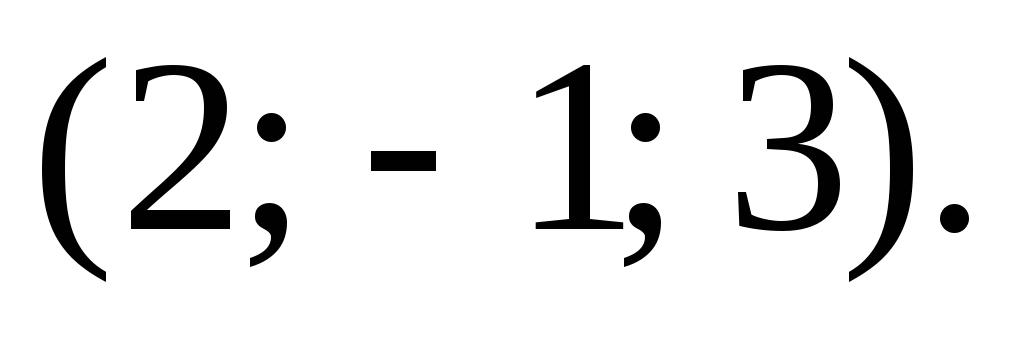
Спроектировать точку
 на прямую
на прямую Ответ:
Ответ:
Спроектировать ось
 на плоскость
на плоскость Ответ:
Ответ:
Найти расстояние от точки
 до плоскости
до плоскости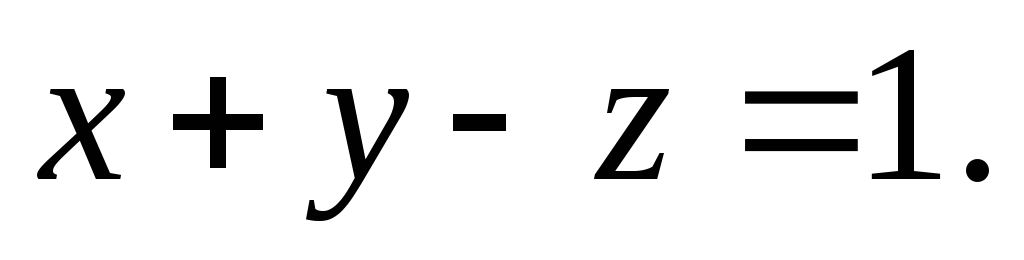 Ответ:
Ответ:
Найти расстояние между плоскостями
 и
и Ответ:
Ответ:
Составить уравнение плоскости, расположенной на одинаковых расстояниях от плоскостей
 и
и Ответ:
Ответ:
На оси ординат найти точку, равноудалённую от плоскостей
 и
и Ответ:
Ответ: и
и
Найти расстояние от точки
 до прямой
до прямой Ответ: 5.
Ответ: 5.
Найти расстояние от начала координат до прямой


 Ответ:
Ответ:
Найти расстояние между прямыми
 и
и
 Ответ:
Ответ:

Найти расстояние между прямыми
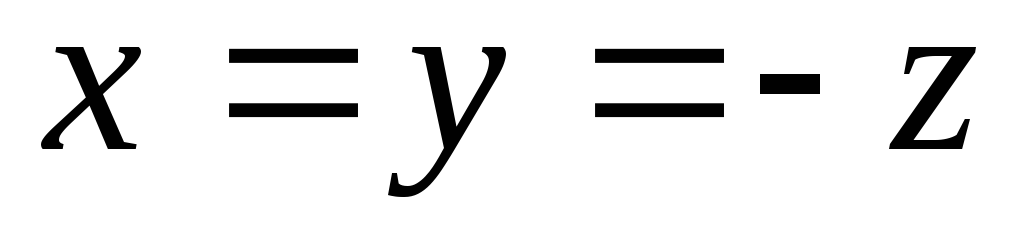 и
и

 Ответ:
Ответ:
Найти расстояние между прямой


 и осью абсцисс. Ответ:
и осью абсцисс. Ответ:
Ребро куба равно
 Найти расстояние между скрещивающимися
диагональю куба и диагональю грани
куба. Ответ:
Найти расстояние между скрещивающимися
диагональю куба и диагональю грани
куба. Ответ:
Боковые грани правильной шестиугольной призмы являются квадратами со стороной
 Вычислить расстояние между скрещивающимися
диагоналями двух смежных граней призмы.
Ответ:
Вычислить расстояние между скрещивающимися
диагоналями двух смежных граней призмы.
Ответ:
На прямой


 найти точку, удалённую от оси абсцисс
на расстояние, равное 5. Ответ:
найти точку, удалённую от оси абсцисс
на расстояние, равное 5. Ответ: или
или
На оси абсцисс найти все точки, равноудалённые от прямых
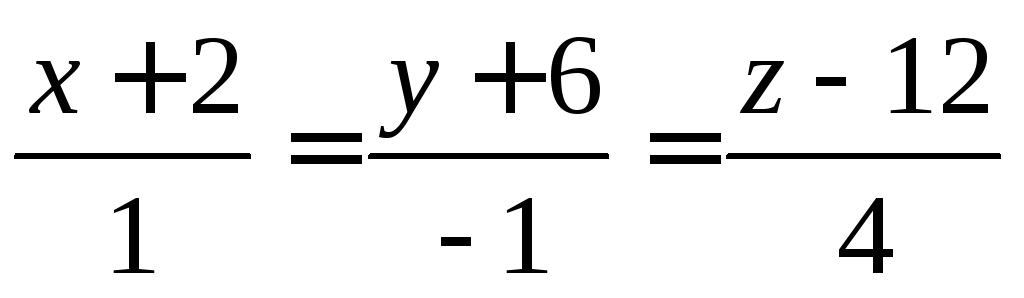 и
и Ответ:
Ответ: и
и
Выяснить взаимное расположение плоскостей: а)

 и
и б)
б)
 и
и в)
в)
 и
и Ответ: а) пересекаются по параллельным
прямым; б) пересекаются в точке; в)
проходят через одну прямую.
Ответ: а) пересекаются по параллельным
прямым; б) пересекаются в точке; в)
проходят через одну прямую.Составить уравнение биссектрисы
 треугольника
треугольника в котором
в котором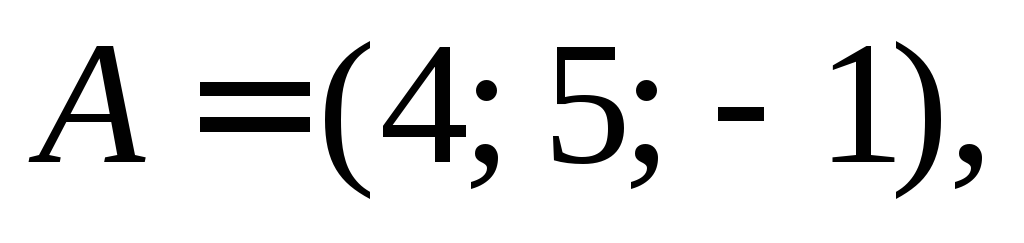

 Ответ:
Ответ:
Найти угол между гиперплоскостями
 и
и (в четырёхмерном пространстве). Ответ:
(в четырёхмерном пространстве). Ответ:
Спроектировать точку
 на гиперплоскость
на гиперплоскость (в четырёхмерном пространстве). Ответ:
(в четырёхмерном пространстве). Ответ:
Найти точку, симметричную точке
 относительно прямой
относительно прямой Ответ:
Ответ:
Даны точки
 и
и На оси абсцисс найти точку
На оси абсцисс найти точку такую, что площадь треугольника
такую, что площадь треугольника равна 2. Ответ:
равна 2. Ответ: и
и
Даны точки
 и
и На плоскости
На плоскости найти точку
найти точку такую, что
такую, что – равнобедренный прямоугольный
треугольник с гипотенузой
– равнобедренный прямоугольный
треугольник с гипотенузой Ответ:
Ответ: и
и
Даны прямые
 и
и Составить уравнение общего перпендикуляра
к этим прямым, пересекающего данные
прямые. Ответ:
Составить уравнение общего перпендикуляра
к этим прямым, пересекающего данные
прямые. Ответ:
Через точку
 провести прямую, пересекающую прямые
провести прямую, пересекающую прямые и
и Ответ:
Ответ:
