1) Определение обыкновенного дифференциального уравнения (ду) 1-го порядка.

Дифференциальным уравнением (ДУ) называют равенство, содержащее независимые переменные, искомую функцию и её производные (или дифференциалы). Во введении отмечено, что уравнение, содержащее ,где есть некоторая функция независимой переменной ,называют дифференциальным уравнением. Запись вида: =0

2) Определение решения и общего решения ДУ 1-го порядка

Решение ДУ – любая функция, которая, будучи подставлена в исходную запись уравнения, обращает его в тождество! Решение дифференциального уравнения 1-го порядка, зависящее от произвольной постоянной величины называется общим решением уравнения. Общее решение определяет бесчисленное множество интегральных кривых уравнения

3) Определение общего интеграла ДУ 1-го порядка

Решается полученное ДУ первого порядка, находится общее решение или общий интеграл. Общий интеграл задается формулой .

4)Определение интегральной кривой ДУ 1-го порядка

Интегральная кривая – это график решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.

5) Определение частного решения дифференциального уравнения 1-го порядка.

Решение дифференциального уравнения 1-го порядка, полученное из общего решения при некотором (частном) значении произвольной постоянной величины ,называется частным решением уравнения. Частное решение определяет одну из множества интегральных кривых уравнения. Тогда решение уравнения, записанное в виде: ,называется частным решением.

6)6. Поле направлений для уравнения . Использование «Поля направлений» и «Изоклин» для предварительной оценки вида интегральных кривых

В прямоугольной системе координат выделим точку .Пусть решением уравнения есть функция: –интегральная кривая этого уравнения. Как и в рассмотренном выше примере, число будем рассматривать как угловой коэффициент касательной к кривой в выделенной точке

плоскости ,определяющий некоторое направление. Таким образом, для любой точки плоскости ,принадлежащей области определения функции ,уравнение устанавливает направление, то есть порождает поле направлений. В каждой точке этого поля направление отметим стрелкой.

Процесс построения поля направлений можно существенно усовершенствовать, если воспользоваться изоклинами – кривыми линиями, каждая точка которых отражает одно и то же направление поля направлений. Для построения на плоскости изоклины поля направлений, соответствующей угловому коэффициенту ,нужно построить график функции: .Выбирая на построенном графике достаточное число точек, отмечаем в каждой из них направление поля, соответствующее угловому коэффициенту .Построив несколько изоклин с отмеченными направлениями поля, можно получить вполне приемлемое представление о множестве решений (интегральных кривых) заданного дифференциального уравнения.

Анализируя процесс построения поля направлений для любого уравнения ,приходим к выводу: каждое дифференциальное уравнение имеет бесчисленное множество решений!

Для иллюстрации применения изоклин и поля направлений рассмотрим несколько примеров для конкретных дифференциальных уравнений.

Пример 1–01: Методом изоклин построить приближенно семейство интегральных кривых для дифференциального уравнения: .

Решение: 1). Если принять ,то уравнение изоклины для заданного уравнения: –уравнение окружности, радиус которой равен 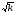.Для примера ограничимся значениям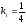и: ,,и .На рисунке этим значениям соответствуют окружности радиусов: ,и .

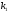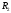2). Из произвольных точек окружностей (изоклин) проводим стрелки: для окружности радиуса с угловым коэффициентом ,для окружности радиуса с угловым коэффициентом 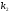и для окружности радиуса с угловым коэффициентом .

3). Используя набор лекал различной кривизны, построим интегральные кривые, пересекающие каждую из окружностей-изоклин под определённым углом: первую под углом, определяемым угловым коэффициентом, вторую под углом, определяемым угловым коэффициентом и третью под углом, определяемым угловым коэффициентом.

Ответ: на рисунке показаны три интегральных кривых.