
- •Степень заполнения примесных уровней
- •Концентрация электронов
- •Концентрация дырок
- •Концентрации электронов и дырок
- •Интегралы Ферми-Дирака в примесном полупроводнике
- •Невырожденный примесный полупроводник
- •Собственный полупроводник
- •Механизмы рассеяния электронов и дырок
- •Уравнение Больцмана
- •Время релаксации
- •Рассеяние на ионах примеси
- •Рассеяние на ионах примеси
- •Рассеяние на атомах примеси и дислокациях
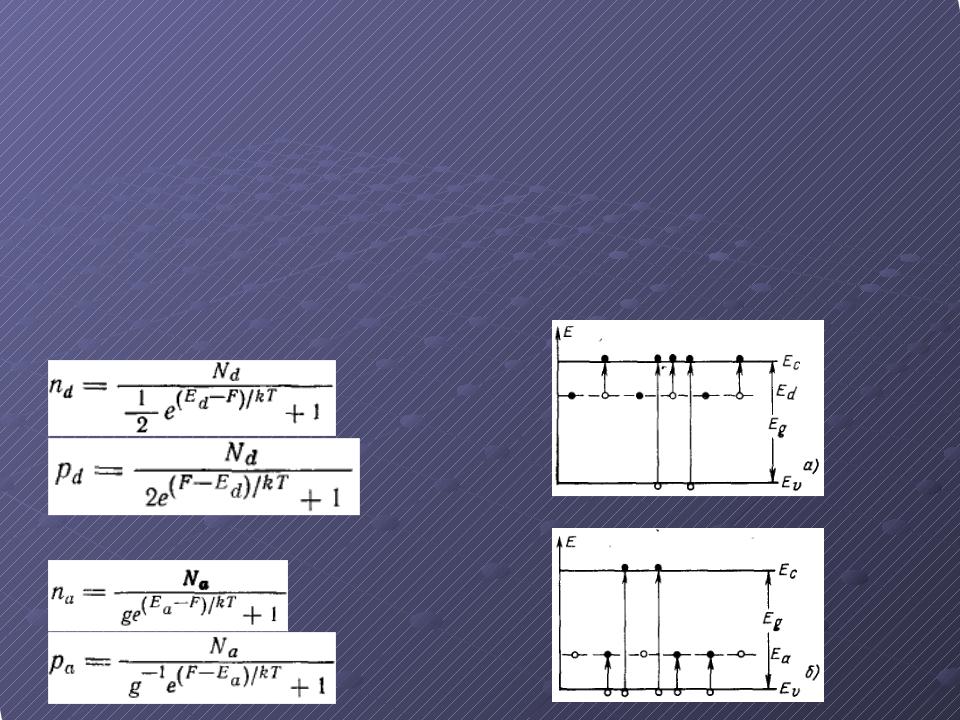
Степень заполнения примесных уровней
Если Nd, Na – концентрации донорной и акцепторной примесей, nd, pa – концентрации электронов и дырок в
донорном и акцепторном п/п, соответственно.
Концентрация положительно и отрицательно заряженных
 ионов в донорном и акцепторном п/п, соответственно,
ионов в донорном и акцепторном п/п, соответственно,
 вычисляется:
вычисляется: 







pd=Nd-nd и na=Na-pa .  ДОНОРНЫЙ ПОЛУПРОВОДНИК:
ДОНОРНЫЙ ПОЛУПРОВОДНИК:
АКЦЕПТОРНЫЙ ПОЛУПРОВОДНИК: 

Концентрация электронов
Концентрация электронов при термодинамическом равновесии:
 Введем безразмерные величины:
Введем безразмерные величины:
С учетом величин:
- Интеграл Ферми-Дирака с индексом ½.
- Эффективная плотность состояний в зоне проводимости. 

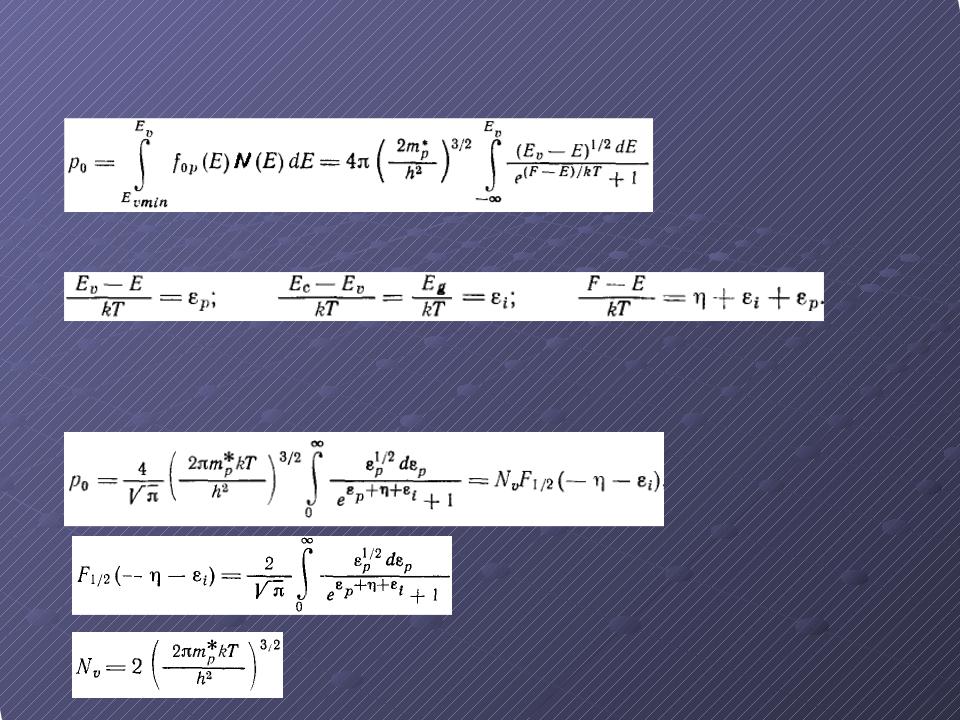
Концентрация дырок
Концентрация дырок при термодинамическом равновесии:
 Введем безразмерные величины:
Введем безразмерные величины:
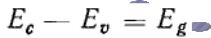 - Ширина запрещенной зоны. С учетом безразмерных величин:
- Ширина запрещенной зоны. С учетом безразмерных величин: 
- Интеграл Ферми-Дирака для валентной зоны.
- Эффективная плотность состояний в валентной зоне. 



Концентрации электронов и дырок
Если считать, что |
то при Т=300К Nc=Nv=2,5*1019 |
см-3 . |
|
Донорный полупроводник. Введем |
|
обозначение: |
|
Концентрация электронов на уровне донорной
примеси:
Количество положительных ионов:
Акцепторный полупроводник. Введем  обозначение:
обозначение: 
Концентрация дырок на уровне акцепторной примеси:
Количество отрицательных ионов

Интегралы Ферми-Дирака в примесном полупроводнике
1. Невырожденный полупроводник (статистика  Больцмана)
Больцмана) 






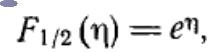



Равновесные концентрации электронов и дырок:

2. Сильно вырожденный полупроводник:
3. Переход от невырожденного к вырожденному:

Невырожденный примесный полупроводник
Можно считать, что донорный полупроводник невырожден, если 





 или
или


Для электронов в зоне проводимости с энергией E=>Ec 

 некоторыми компонентами в функции распределения
некоторыми компонентами в функции распределения 
 Ферми-Дирака можно пренебречь:
Ферми-Дирака можно пренебречь: 


Интеграл Ферми-Дирака запишется в виде:
Равновесные концентрации электронов и дырок:

Собственный полупроводник
В собственном п/п электроны и дырки появляются парами, поэтому концентрации свободных электронов и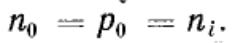
 Собственная концентрация
Собственная концентрация 
Тогда:
Отсюда следует: 
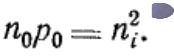


Механизмы рассеяния электронов и дырок
-Рассеяние на тепловых колебаниях решетки; -Рассеяние на атомах и ионах примеси; -Рассеяние на вакансиях, дислокациях и т.д.
Количество рассеянных электронов в единицу времени:
Эффективное сечение рассеяния:
Вероятность столкновения
(рассеяния):
Время и длину свободного пробега можно выразить через
эффективное |
Вероятность рассеяния |
|
на единичном интервале |
Полная вероятность рассеяния |
пути |
|
|
Полная длина свободного пробега |
|

Уравнение Больцмана
Поведение носителей заряда при термодинамическом равновесии  определяется функцией распределения, которая в общем случае
определяется функцией распределения, которая в общем случае  зависит от энергии частиц:
зависит от энергии частиц: 










Во внешнем электрическом поле система движущихся части определяется функцией f=f(k,r,t). Уравнение Больцмана  описывает изменение функции распределения во времени:
описывает изменение функции распределения во времени:
В равновесии:
