Лабораторная работа № 18 законы столкновений

Цель работы:

Исследование законов сохранения импульса и энергии при упругом и неупругом соударениях двух тел.

Оборудование:

Установка, включающая в себя рельс, по которому могут скользить тележки; грузы известной массы; световые барьеры; электронный блок Cobra3; компьютер.

Продолжительность работы– 4 часа.

Теоретическая часть.

Силы взаимодействия между сталкивающимися телами столь велики, что внешними силами, действующими на них, как правило, можно пренебречь. Это позволяет систему тел в процессе их соударения приближенно рассматривать как замкнутую системуи применять к ней законы сохранения. Различают два предельных типа удара:абсолютно упругий и абсолютно неупругий.

Абсолютно упругий удар – столкновение тел, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия вначале переходит в потенциальную энергию упругой деформации. Затем форма тела постепенно возвращается к первоначальной. При этом потенциальная энергия упругой деформации переходит в кинетическую энергию, и тела отталкиваются друг от друга. Если после удара тела двигаются поступательно, они разлетаются со скоростями, модуль и направление которых определяются двумя условиями:сохранением полной энергии и сохранением полного импульса системы тел .

В качестве примера рассмотрим абсолютно упругое столкновение двух шаров, движущихся навстречу друг другу вдоль линии, соединяющей их центры масс (центральный удар). Обозначим массы шаров и, скорости шаров до удараи, а скорости после удараи(рис.1).

Рис. 1. Схема столкновения при абсолютно упругом центральном ударе двух шаров.

Согласно закону сохранения импульса () и учитывая, что общая кинетическая энергия () шаров до и после удара одинакова, можно записать:

(1)

(2)

Равенства (1) и (2) запишем в виде:

. (3)

. (4)

Из равенств (3) и (4) следует, что: . (5)

Скорости шаров после удара получим, умножив (5) на и вычтя результат из (3), а затем умножив (5) наи сложив результат с (3):

,. (6)

Используя соотношения (6), определим проекцииивекторовина осьx(рис. 1). При:

,. (7)

Из этих выражений понятно, что изображенное на рис.1 столкновение соответствует случаю >.

Проекции импульсов шаров после упругого столкновения найдем умножив соотношения (7) на массы и.

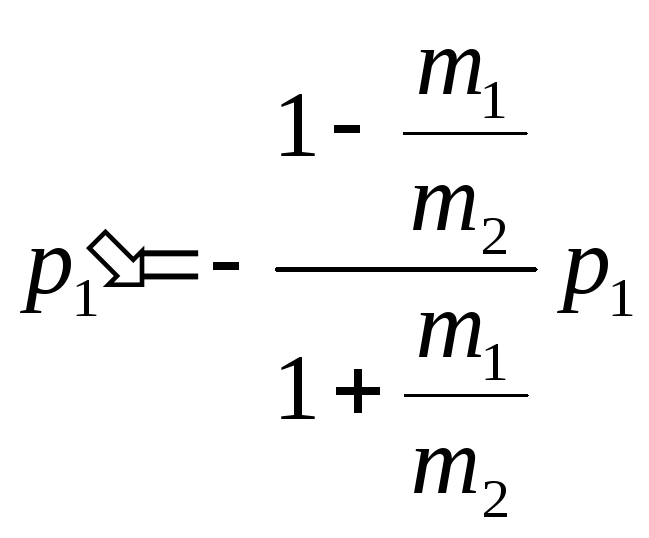,. (8)

Отсюда получим выражения для кинетической энергии шаров () после упругого столкновения при:

,. (9)

Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Происходит неупругая деформация тел и их слипание. Кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся.При абсолютно неупругом ударе сохраняется лишь импульс, механическая энергия не сохраняется: имеет место закон сохранения суммарной энергии различных видов – механической и внутренней.

Рассмотрим неупругое столкновение двух шаров массами и, скорости которых до удараи. После удара шары, объединившись, двигаются со скоростью. Согласно закону сохранения импульса:

, или. (10)

откуда

. (11)

Рассматривая движение шаров вдоль прямой, проходящей через их центры масс, спроектируем соотношение (10) на ось х, направление которой совпадает с вектором.

При условии, что , получаем проекцию импульса шаров после неупругого удара

. (12)

Кинетическая энергии шаров до удара () и после удара () соответственно равны

и, (13)

где и– кинетические энергии шаров до удара.

Если ударяемое тело было неподвижно (), то из (11) и (13) следует, что:

. (14)

Убыль кинетической энергии равна увеличению внутренней энергии шаров в процессе удара. Относительное значение этой величины получим из соотношения (14):

. (15)